asymptotics
Determine Markov chain asymptotics
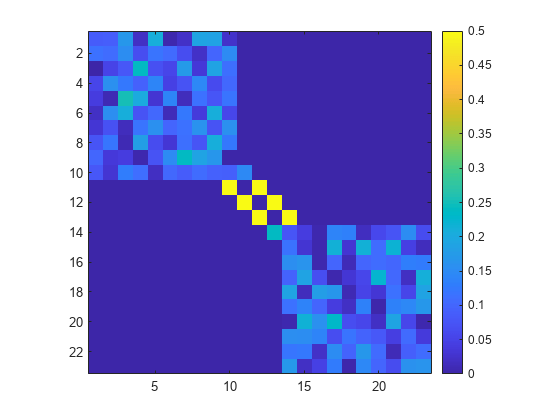
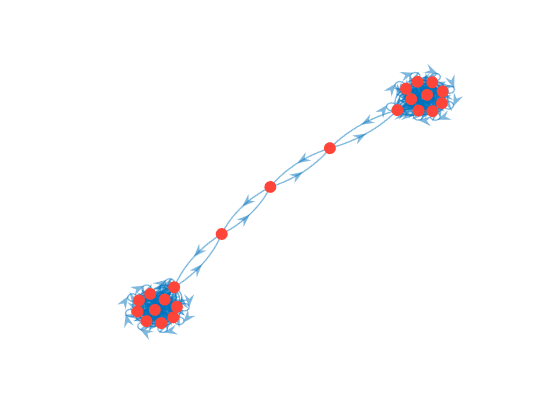
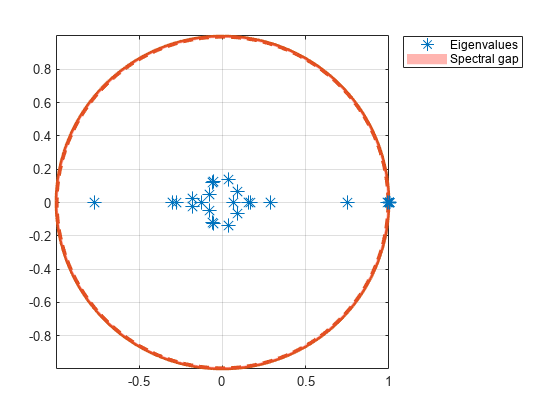
Description
Examples
Input Arguments
Output Arguments
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
[2] Horn, R., and C. R. Johnson. Matrix Analysis. Cambridge, UK: Cambridge University Press, 1985.
[3] Seneta, E. Non-negative Matrices and Markov Chains. New York, NY: Springer-Verlag, 1981.
Version History
Introduced in R2017b