classify
Classify Markov chain states
Description
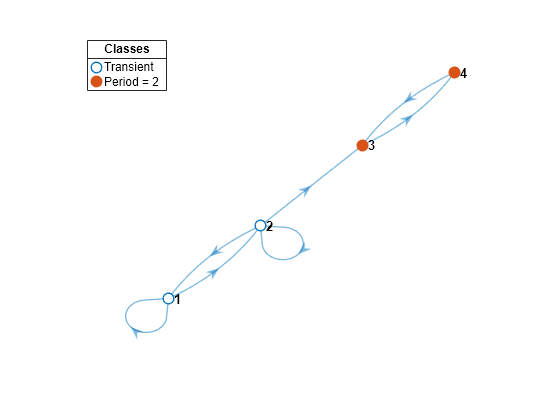
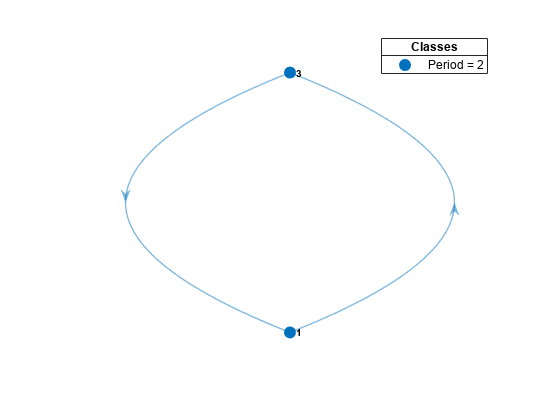
bins = classify(mc)mc into disjoint communicating classes and returns the class labels bins identifying the communicating class to which each state belongs.
[ additionally returns the states in each class (bins,ClassStates,ClassRecurrence,ClassPeriod] = classify(mc)ClassStates), whether the classes are recurrent (ClassRecurrence), and class periods (ClassPeriod).
Examples
Input Arguments
Output Arguments
More About
Algorithms
classifydetermines recurrence and transience from the outdegree of the supernode associated with each communicating class in the condensed digraph [1]. An outdegree of 0 corresponds to recurrence; an outdegree that is greater than 0 corresponds to transience. Seegraphplot.classifydetermines periodicity using a breadth-first search of cycles in the associated digraph, as in [3]. Class period is the greatest common divisor of the lengths of all cycles originating at any state in the class.
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
[2] Horn, R., and C. R. Johnson. Matrix Analysis. Cambridge, UK: Cambridge University Press, 1985.
[3] Jarvis, J. P., and D. R. Shier. "Graph-Theoretic Analysis of Finite Markov Chains." In Applied Mathematical Modeling: A Multidisciplinary Approach. Boca Raton: CRC Press, 2000.
Version History
Introduced in R2017b