Differentiator Filter

R2026b

Direct form FIR fullband differentiator filter

• 

Differentiator Filter block

To add a block to a model, double-click the canvas and start typing the block name. Then, select the block from the list.

Libraries:
DSP System Toolbox / Filtering / Filter Designs

Description

The Differentiator Filter block applies a fullband differentiator filter on the input signal to differentiate all its frequency components. The block uses an FIR equiripple filter design to design the differentiator filter. The ideal frequency response of the differentiator is $$D(\omega )=j\omega$$ for $$-\pi \le \omega \le \pi$$.

You can design the filter with a minimum order or with a specific order.

This block also supports SIMD code generation. For details, see Code Generation.

Examples

Group Delay Estimation in Simulink

Estimate the group delay of a filter in Simulink®.

• Open Model

Ports

Input

Input — Data input

vector | matrix

Specify the data input as a vector or a matrix. If the input signal is a matrix, each column of the matrix is treated as an independent channel.

This block supports variable-size input, enabling you to change the channel length during simulation.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Complex Number Support: Yes

Output

Output — Differentiator filter output

vector | matrix

Differentiator filter output, returned as a vector or a matrix.

The output port properties, such as data type, complexity, and dimension are identical to the input port properties.

Data Types: single | double | fixed point
Complex Number Support: Yes

Parameters

Main Tab

Design minimum order filter — Design minimum order filter

on (default) | off

When you select this check box, the block designs a filter with the minimum order and with the passband ripple that you specify in Maximum passband ripple (dB). When you clear this check box, specify the order of the filter in Filter order.

Filter order — Order of differentiator filter

31 (default) | odd positive integer

Specify the order of the differentiator filter as an odd positive integer.

Dependencies

To enable this parameter, clear the Design minimum order filter parameter.

Maximum passband ripple (dB) — Maximum passband ripple

0.1 (default) | positive scalar

Specify the maximum ripple of the filter response in the passband as a real positive scalar in dB.

Scale filter coefficients — Scale filter coefficients

off (default) | on

When you select this check box, the blocks scales the filter coefficients to preserve the input dynamic range. By default, this check box is not selected.

View Filter Response — View filter response

button (default)

Click this button to open the Filter Visualization Tool (fvtool) and display the magnitude and phase response of the Differentiator Filter block. The response is based on the block dialog box parameters. Changes made to these parameters update FVTool.

To update the magnitude response while FVTool is running, modify the dialog box parameters and click Apply.

Simulate using — Simulate using

Interpreted execution (default) | Code generation

Specify the type of simulation to run. You can set this parameter to:

• Interpreted execution (default)

  Simulate model using the MATLAB^®  interpreter. This option shortens startup time and has faster simulation speed than Code generation.

• Code generation

  Simulate model using generated C code. The first time you run a simulation, Simulink^® generates C code for the block. The C code is reused for subsequent simulations, as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.

Data Types Tab

Rounding mode — Rounding mode

Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero

Specify the rounding method for the output fixed-point operations. The rounding methods are Ceiling, Convergent, Floor, Nearest, Round, Simplest, and Zero. The default is Floor.

Coefficients — Coefficients

fixdt(1,16) (default) | fixdt(1,16,0) | <data type expression>

Specify the fixed-point data type of the coefficients as one of the following:

• fixdt(1,16) — Signed fixed-point data type of word length 16 with binary point scaling. The block determines the fraction length automatically from the coefficient values such that the coefficients occupy the maximum representable range without overflowing.

• fixdt(1,16,0) — Signed fixed-point data type of word length 16 and fraction length 0. You can change the fraction length to any other integer value.

• <data type expression> — Specify the data type using an expression that evaluates to a data type object, for example, numeric type (fixdt([ ],16, 15)). Specify the sign mode of this data type as [ ] or true.

• Refresh Data Type — Refresh to the default data type.

Click the Show data type assistant button to display the data type assistant, which helps you set the stage input parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

The word length of the output is same as the word length of the input. The fraction length of the output is computed such that the entire dynamic range of the output can be represented without overflow. For details on how the block computes the fraction length, see Fixed-Point Precision Rules for Avoiding Overflow in FIR Filters.

Block Characteristics

Data Types	double | fixed point | integer | single
Direct Feedthrough	no
Multidimensional Signals	no
Variable-Size Signals	yes
Zero-Crossing Detection	no

Programmatic Use: Add Block

To add the block programmatically, use the add_block function with one of these library block paths as the source.

"dspfdesign/Differentiator Filter"

Example: add_block("dspfdesign/Differentiator Filter","myModel/myBlock",MakeNameUnique="on")

Algorithms

Differentiator Filter

Differentiator computes the derivative of a signal. The frequency response of an ideal differentiator filter is given by $$D(\omega )=j\omega$$, defined over the Nyquist interval $$-\pi \le \omega \le \pi$$.

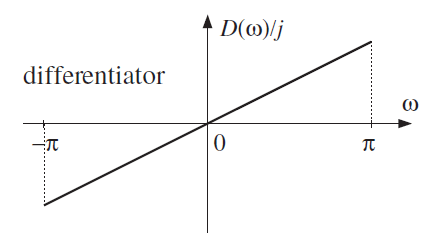
The frequency response is antisymmetric and is linearly proportional to the frequency.

dsp.Differentiator object acts as a differentiator filter. This object condenses the two-step process into one. For the minimum order design, the object uses generalized Remez FIR filter design algorithm. For the specified order design, the object uses the Parks-McClellan optimal equiripple FIR filter design algorithm. The filter is designed as a linear phase Type-IV FIR filter with a Direct form structure.

The ideal differentiator has an antisymmetric impulse response given by $$d(n)=-d(-n)$$. Hence $$d(0)=0$$. The differentiator must have zero response at zero frequency.

Linear-Phase FIR Differentiator Filter

The impulse response of an antisymmetric linear-phase FIR filter is given by $$h(n)=-h(M-1-n)$$, where M is the length of the filter. Because the filter is antisymmetric, you can use this type of FIR filter to design the linear-phase FIR differentiators.

Consider the design of linear-phase FIR differentiators based on the Chebyshev approximation criterion.

If M is odd, the real-valued frequency response of the FIR filter, H_r(ω), has the characteristics that H_r(0) = 0 and H_r(π) = 0. This filter satisfies the condition of zero response at zero frequency. However, it is not fullband because H_r(π) = 0. This differentiator has a linear response over the limited frequency range [0 2πf_p], where f_p is the bandwidth of the differentiator. The absolute error between the desired response and the Chebyshev approximation increases as ω increases from 0 to 2πf_p.

If M is even, the real-valued frequency response of the FIR filter, H_r(ω), has the characteristics that H_r(0) = 0 and H_r(π) ≠ 0. This filter satisfies the condition of zero response at zero frequency. It is fullband and this design results in a significantly smaller approximation error than comparable odd-length differentiators. Hence, even-length (odd order) differentiators are preferred in practical systems.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

The Differentiator Filter block supports SIMD code generation using Intel AVX2 code replacement library when the input signal has a data type of single or double.

The SIMD technology significantly improves the performance of the generated code. For more information, see SIMD Code Generation. To generate SIMD code from this block, see Use Intel AVX2 Code Replacement Library to Generate SIMD Code from Simulink Blocks.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2015b