fit
Fit curve or surface to data
Syntax
Description
fitobject = fit(x,y,fitType,fitOptions)fitOptions object.
fitobject = fit(x,y,fitType,Name=Value)fitType with additional options specified by one or more Name=Value pair arguments. Use fitoptions to display available property names and default values for the specific library model.
Examples
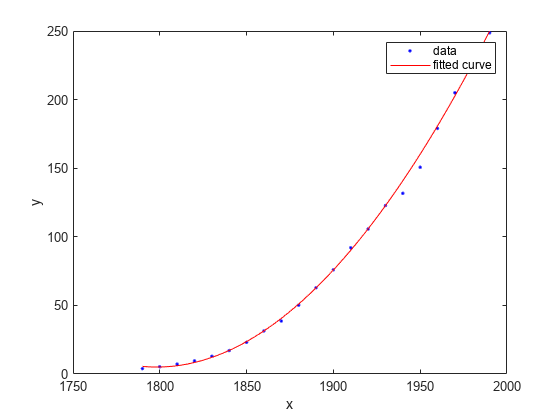
Load the census sample data set.
load census;The vectors pop and cdate contain data for the population size and the year the census was taken, respectively.
Fit a quadratic curve to the population data.
f=fit(cdate,pop,'poly2')f =
Linear model Poly2:
f(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+04 (1.964e+04, 2.262e+04)
f contains the results of the fit, including coefficient estimates with 95% confidence bounds.
Plot the fit in f together with a scatter plot of the data.
plot(f,cdate,pop)

The plot shows that the fitted curve closely follows the population data.
Load the franke sample data set.
load frankeThe vectors x, y, and z contain data generated from Franke's bivariate test function, with added noise and scaling.
Fit a polynomial surface to the data. Specify a degree of two for the x terms and degree of three for the y terms.
sf = fit([x, y],z,'poly23')sf =
Linear model Poly23:
sf(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
Coefficients (with 95% confidence bounds):
p00 = 1.118 (0.9149, 1.321)
p10 = -0.0002941 (-0.000502, -8.623e-05)
p01 = 1.533 (0.7032, 2.364)
p20 = -1.966e-08 (-7.084e-08, 3.152e-08)
p11 = 0.0003427 (-0.0001009, 0.0007863)
p02 = -6.951 (-8.421, -5.481)
p21 = 9.563e-08 (6.276e-09, 1.85e-07)
p12 = -0.0004401 (-0.0007082, -0.0001721)
p03 = 4.999 (4.082, 5.917)
sf contains the results of the fit, including coefficient estimates with 95% confidence bounds.
Plot the fit in sf together with a scatterplot of the data.
plot(sf,[x,y],z)

Load and plot the data, create fit options and fit type using the fittype and fitoptions functions, then create and plot the fit.
Load and plot the data in census.mat.
load census plot(cdate,pop,'o')
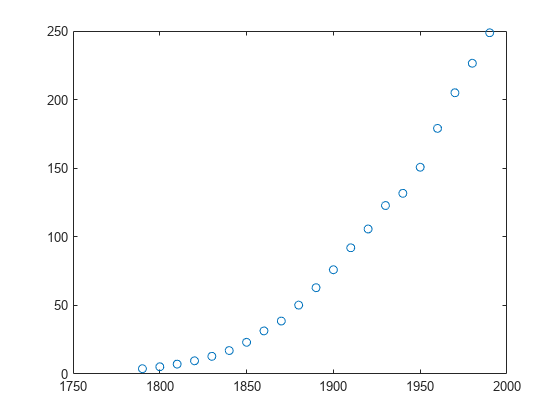
Create a fit options object and a fit type for the custom nonlinear model , where a and b are coefficients and n is a problem-dependent parameter.
fo = fitoptions('Method','NonlinearLeastSquares',... 'Lower',[0,0],... 'Upper',[Inf,max(cdate)],... 'StartPoint',[1 1]); ft = fittype('a*(x-b)^n','problem','n','options',fo);
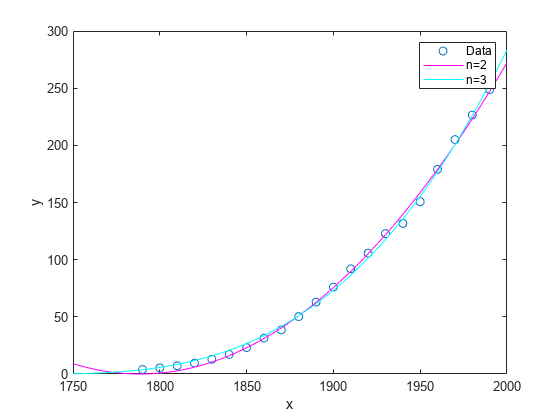
Fit the data using the fit options and a value of n = 2.
[curve2,gof2] = fit(cdate,pop,ft,'problem',2)curve2 =
General model:
curve2(x) = a*(x-b)^n
Coefficients (with 95% confidence bounds):
a = 0.006092 (0.005743, 0.006441)
b = 1789 (1784, 1793)
Problem parameters:
n = 2
gof2 = struct with fields:
sse: 246.1543
rsquare: 0.9980
dfe: 19
adjrsquare: 0.9979
rmse: 3.5994
Fit the data using the fit options and a value of n = 3.
[curve3,gof3] = fit(cdate,pop,ft,'problem',3)curve3 =
General model:
curve3(x) = a*(x-b)^n
Coefficients (with 95% confidence bounds):
a = 1.359e-05 (1.245e-05, 1.474e-05)
b = 1725 (1718, 1731)
Problem parameters:
n = 3
gof3 = struct with fields:
sse: 232.0058
rsquare: 0.9981
dfe: 19
adjrsquare: 0.9980
rmse: 3.4944
Plot the fit results with the data.
hold on plot(curve2,'m') plot(curve3,'c') legend('Data','n=2','n=3') hold off
Load the carbon12alpha nuclear reaction sample data set.
load carbon12alphaangle is a vector of emission angles in radians. counts is a vector of raw alpha particle counts that correspond to the angles in angle.
Display a scatter plot of the counts plotted against the angles.
scatter(angle,counts)
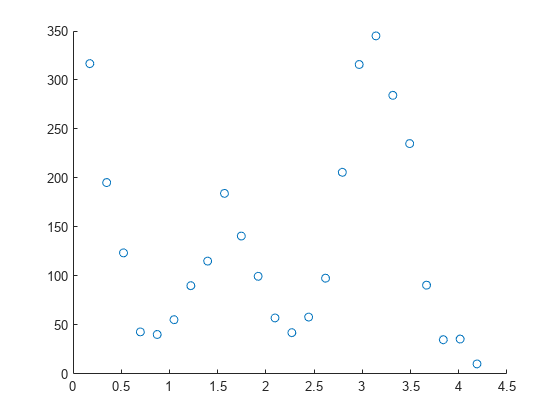
The scatter plot shows that the counts oscillate as the angle increases between 0 and 4.5. To fit a polynomial model to the data, specify the fitType input argument as "poly#" where # is an integer from one to nine. You can fit models of up to nine degrees. See List of Library Models for Curve and Surface Fitting for more information.
Fit a fifth-degree, seventh-degree, and ninth-degree polynomial to the nuclear reaction data. Return the goodness-of-fit statistics for each fit.
[f5,gof5] = fit(angle,counts,"poly5"); [f7,gof7] = fit(angle,counts,"poly7"); [f9,gof9] = fit(angle,counts,"poly9");
Generate a vector of query points between 0 and 4.5 by using the linspace function. Evaluate the polynomial fits at the query points, and then plot them together with the nuclear reaction data.
xq = linspace(0,4.5,1000); figure hold on scatter(angle,counts,"k") plot(xq,f5(xq)) plot(xq,f7(xq)) plot(xq,f9(xq)) ylim([-100,550]) legend("original data","fifth-degree polynomial","seventh-degree polynomial","ninth-degree polynomial")
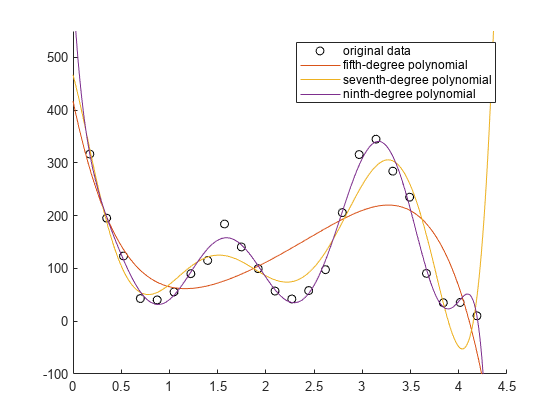
The plot indicates that the ninth-degree polynomial follows the data most closely.
Display the goodness-of-fit statistics for each fit by using the struct2table function.
gof = struct2table([gof5 gof7 gof9],RowNames=["f5" "f7" "f9"])
gof=3×5 table
sse rsquare dfe adjrsquare rmse
__________ _______ ___ __________ ______
f5 1.0901e+05 0.54614 18 0.42007 77.82
f7 32695 0.86387 16 0.80431 45.204
f9 3660.2 0.98476 14 0.97496 16.169
The sum-of-squares error (SSE) for the ninth-degree polynomial fit is smaller than the SSEs for the fifth-degree and seventh-degree fits. This result confirms that the ninth-degree polynomial follows the data most closely.
Load the census sample data set. Fit a cubic polynomial and specify the Normalize (center and scale) and Robust fitting options.
load census; f = fit(cdate,pop,'poly3','Normalize','on','Robust','Bisquare')
f =
Linear model Poly3:
f(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = -0.4619 (-1.895, 0.9707)
p2 = 25.01 (23.79, 26.22)
p3 = 77.03 (74.37, 79.7)
p4 = 62.81 (61.26, 64.37)
Plot the fit.
plot(f,cdate,pop)
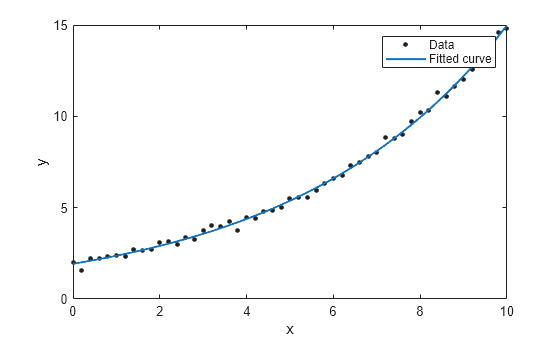
Generate data with an exponential trend and then fit the data using a single-term exponential. Plot the fit and data.
rng(2,"twister"); x = (0:0.2:10)'; y = 2*exp(0.2*x) + 0.2*randn(size(x)); % Without constraints fitresult1 = fit(x,y,"exp1"); plot(fitresult1,x,y); hold on
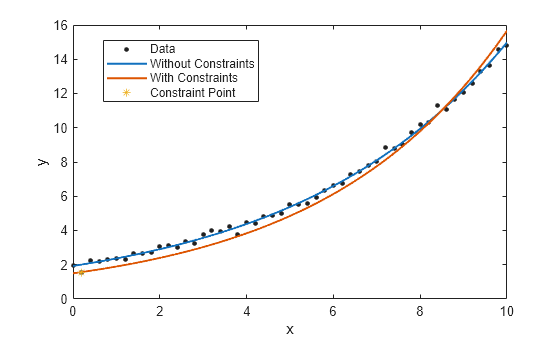
Fit a new exponential curve with the second data point as a constraint. As it is a non-linear fittype, the Algorithm must be specified as "Interior-Point" to fit with constraint points. If it is not specified, the software internally switches to use the "Interior-Point" algorithm.
% With constraints point = [x(2) y(2)]; fitresult2 = fit(x,y,"exp1",ConstraintPoints=point,Algorithm="Interior-Point"); plot(fitresult2); plot(point(:,1),point(:,2),"*"); legend("Data","Without Constraints","With Constraints", ... "Constraint Point",Location="best");
Define a function in a file and use it to create a fit type and fit a curve.
Define a function in a MATLAB® file.
type piecewiseLine.mfunction y = piecewiseLine(x,a,b,c,k)
% PIECEWISELINE A line made of two pieces
y = zeros(size(x));
% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
if x(i) < k
y(i) = a + b.*x(i);
else
y(i) = a + b*k + c.*(x(i)-k);
end
end
end
Save the file.
Define some data and create a fit type specifying the function piecewiseLine.
x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;... 0.96;0.96;0.16;0.97;0.96]; y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;... 0.15;-0.046;0.17;-0.091;-0.071]; ft = fittype('piecewiseLine( x, a, b, c, k )')
ft =
General model:
ft(a,b,c,k,x) = piecewiseLine( x, a, b, c, k )
The inputs to ft are the coefficients in alphabetical order, followed by the independent variables. See Input Order for Anonymous Functions to learn more.
If you want to control the order of coefficients, then use an anonymous function input. For example, to change the order of the a and b coefficients:
ft = fittype(@(b,a,c,k,x) piecewiseLine(x,a,b,c,k))
You must specify the independent variable x last.
Create a fit using the fit type ft and plot the results.
f = fit(x, y, ft, 'StartPoint', [1, 0, 1, 0.5]);
plot(f, x, y)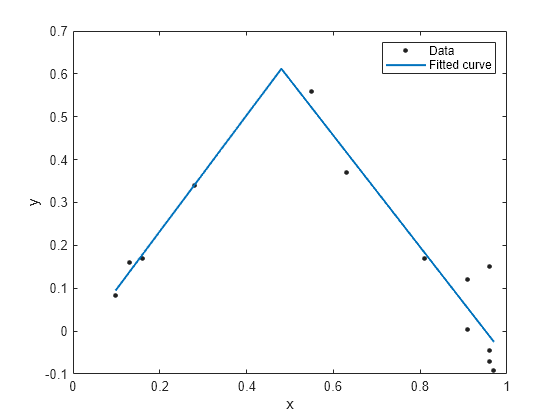
You can define the excluded points as variables before supplying them as inputs to the fit function. The following steps recreate the fits in the previous example and allow you to plot the excluded points as well as the data and the fit.
Load data and define a custom equation and some start points.
[x, y] = titanium;
gaussEqn = 'a*exp(-((x-b)/c)^2)+d'gaussEqn = 'a*exp(-((x-b)/c)^2)+d'
startPoints = [1.5 900 10 0.6]
startPoints = 1×4
1.5000 900.0000 10.0000 0.6000
Define two sets of points to exclude, using an index vector and an expression.
exclude1 = [1 10 25]; exclude2 = x < 800;
Create two fits using the custom equation, startpoints, and the two different excluded points.
f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude1); f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude2);
Plot both fits and highlight the excluded data.
plot(f1,x,y,exclude1)
title('Fit with data points 1, 10, and 25 excluded')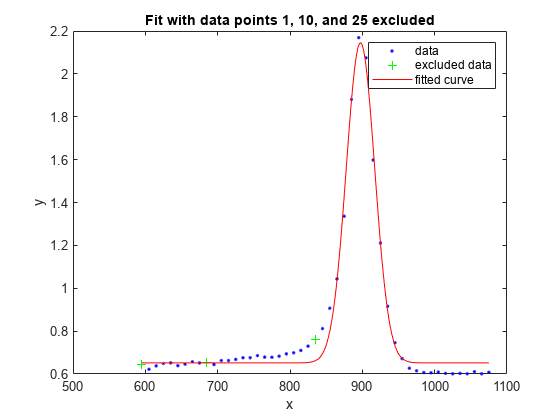
figure;
plot(f2,x,y,exclude2)
title('Fit with data points excluded such that x < 800')
For a surface fitting example with excluded points, load some surface data and create and plot fits specifying excluded data.
load franke f1 = fit([x y],z,'poly23', 'Exclude', [1 10 25]); f2 = fit([x y],z,'poly23', 'Exclude', z > 1); figure plot(f1, [x y], z, 'Exclude', [1 10 25]); title('Fit with data points 1, 10, and 25 excluded')
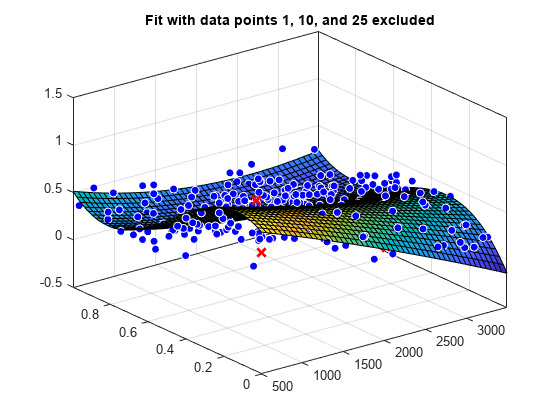
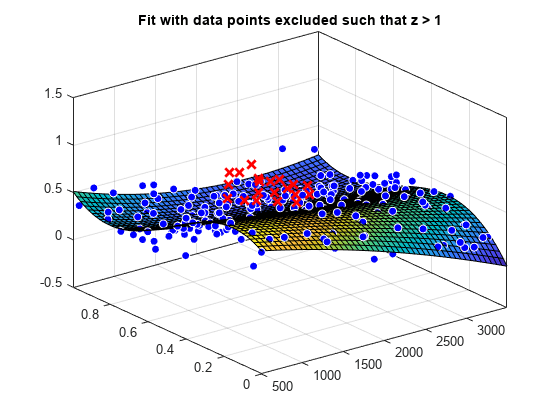
figure plot(f2, [x y], z, 'Exclude', z > 1); title('Fit with data points excluded such that z > 1')
Generate some noisy data using the membrane and randn functions.
n = 41; M = membrane(1,20)+0.02*randn(n); [X,Y] = meshgrid(1:n);
The matrix M contains data for the L-shaped membrane with added noise. The matrices X and Y contain the row and column index values, respectively, for the corresponding elements in M.
Display a surface plot of the data.
figure(1) surf(X,Y,M)
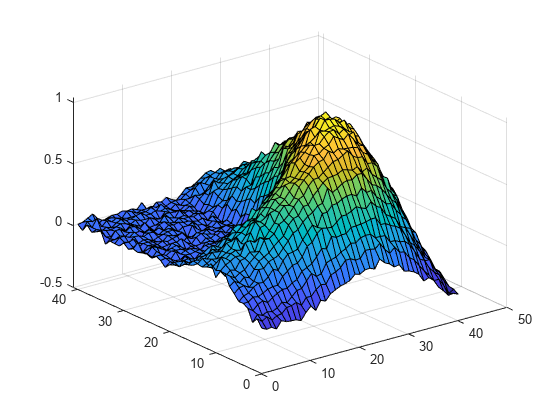
The plot shows a wrinkled L-shaped membrane. The wrinkles in the membrane are caused by the noise in the data.
Fit two surfaces through the wrinkled membrane using linear interpolation. For the first surface, specify the linear extrapolation method. For the second surface, specify the extrapolation method as nearest neighbor.
flinextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="linear"); fnearextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="nearest");
Investigate the differences between the extrapolation methods by using the meshgrid function to evaluate the fits at query points extending outside the convex hull of the X and Y data.
[Xq,Yq] = meshgrid(-10:50); Zlin = flinextrap(Xq,Yq); Znear = fnearextrap(Xq,Yq);
Plot the evaluated fits.
figure(2) surf(Xq,Yq,Zlin) title("Linear Extrapolation") xlabel("X") ylabel("Y") zlabel("M")

figure(3) surf(Xq,Yq,Znear) title("Nearest Neighbor Extrapolation") xlabel("X") ylabel("Y") zlabel("M")
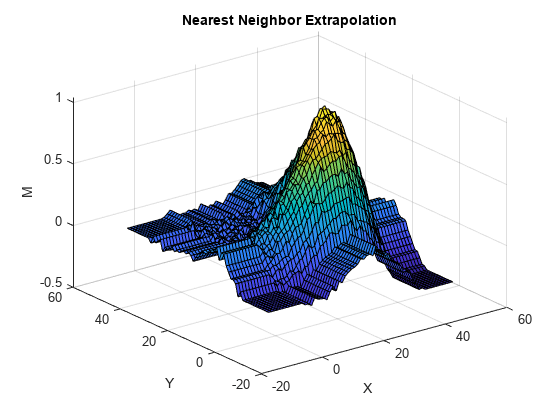
The linear extrapolation method generates spikes outside of the convex hull. The plane segments that form the spikes follow the gradient at points on the convex hull's border. The nearest neighbor extrapolation method uses the data on the border to extend the surface in each direction. This method of extrapolation generates waves that mimic the border.
Fit a smoothing spline curve, and return goodness-of-fit statistics and information about the fitting algorithm.
Load the enso sample data set. The enso sample data set contains data for the monthly averaged atmospheric pressure differences between Easter Island and Darwin, Australia.
load enso;Fit a smoothing spline curve to the data in month and pressure, and return goodness-of-fit statistics and the output structure.
[curve,gof,output] = fit(month,pressure,"smoothingspline");Plot the fitted curve with the data used to fit the curve.
plot(curve,month,pressure); xlabel("Month"); ylabel("Pressure");

Plot the residuals against the x-data (month).
plot(curve,month,pressure,"residuals") xlabel("Month") ylabel("Residuals")

Use the residuals data in the output structure to plot the residuals against the y-data (pressure). To access the residuals field of output, use dot notation.
residuals = output.residuals; plot( pressure,residuals,".") xlabel("Pressure") ylabel("Residuals")

You can use anonymous functions to make it easier to pass other data into the fit function.
Load data and set Emax to 1 before defining your anonymous function:
data = importdata( 'OpioidHypnoticSynergy.txt' );
Propofol = data.data(:,1);
Remifentanil = data.data(:,2);
Algometry = data.data(:,3);
Emax = 1;Define the model equation as an anonymous function:
Effect = @(IC50A, IC50B, alpha, n, x, y) ... Emax*( x/IC50A + y/IC50B + alpha*( x/IC50A )... .* ( y/IC50B ) ).^n ./(( x/IC50A + y/IC50B + ... alpha*( x/IC50A ) .* ( y/IC50B ) ).^n + 1);
Use the anonymous function Effect as an input to the fit function, and plot the results:
AlgometryEffect = fit( [Propofol, Remifentanil], Algometry, Effect, ... 'StartPoint', [2, 10, 1, 0.8], ... 'Lower', [-Inf, -Inf, -5, -Inf], ... 'Robust', 'LAR' ) plot( AlgometryEffect, [Propofol, Remifentanil], Algometry )
For more examples using anonymous functions and other custom models for fitting, see the fittype function.
For the properties Upper, Lower, and StartPoint, you need to find the order of the entries for coefficients.
Create a fit type.
ft = fittype('b*x^2+c*x+a');Get the coefficient names and order using the coeffnames function.
coeffnames(ft)
ans = 3×1 cell
{'a'}
{'b'}
{'c'}
Note that this is different from the order of the coefficients in the expression used to create ft with fittype.
Load data, create a fit and set the start points.
load enso fit(month,pressure,ft,'StartPoint',[1,3,5])
ans =
General model:
ans(x) = b*x^2+c*x+a
Coefficients (with 95% confidence bounds):
a = 10.94 (9.362, 12.52)
b = 0.0001677 (-7.985e-05, 0.0004153)
c = -0.0224 (-0.06559, 0.02079)
This assigns initial values to the coefficients as follows: a = 1, b = 3, c = 5.
Alternatively, you can get the fit options and set start points and lower bounds, then refit using the new options.
options = fitoptions(ft)
options =
nlsqoptions with properties:
StartPoint: []
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Lower: []
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Off'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
options.StartPoint = [10 1 3]; options.Lower = [0 -Inf 0]; fit(month,pressure,ft,options)
ans =
General model:
ans(x) = b*x^2+c*x+a
Coefficients (with 95% confidence bounds):
a = 10.23 (9.448, 11.01)
b = 4.335e-05 (-1.82e-05, 0.0001049)
c = 5.523e-12 (fixed at bound)
Input Arguments
Data to fit, specified as a matrix with either one (curve fitting) or two (surface fitting) columns. You can specify variables in a MATLAB® table using tablename.varname. Cannot contain Inf or NaN. Only the real parts of complex data are used in the fit.
Example: x
Example: [x,y]
Data Types: double
Data to fit, specified as a column vector with the same number of rows as x. You can specify a variable in a MATLAB table using tablename.varname. Cannot contain Inf or NaN. Only the real parts of complex data are used in the fit.
Use prepareCurveData or prepareSurfaceData if your data is not in column vector form.
Data Types: double
Data to fit, specified as a column vector with the same number of rows as x. You can specify a variable in a MATLAB table using tablename.varname. Cannot contain Inf or NaN. Only the real parts of complex data are used in the fit.
Use prepareSurfaceData if your data is not in column vector form. For example, if you have 3 matrices, or if your data is in grid vector form, where length(X) = n, length(Y) = m and size(Z) = [m,n].
Data Types: double
Model type to fit, specified as a character vector or string scalar representing a library model name or MATLAB expression, a string array of linear model terms or a cell array of character vectors of such terms, an anonymous function, or a fittype created with the fittype function. You can use any of the valid first inputs to fittype as an input to fit.
For a list of library model names, see Model Names and Equations.
To a fit custom model, use a MATLAB expression, a cell array of linear model terms, or an anonymous function. You can also create a fittype using the fittype function, and then use it as the value of the fitType input argument. For an example, see Fit a Custom Model Using an Anonymous Function. For examples that use linear model terms, see the fittype function.
Example: "poly2"
Algorithm options constructed using the fitoptions function. This is an alternative to specifying name-value pair arguments for fit options.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: Lower=[0,0],Upper=[Inf,max(x)],StartPoint=[1 1] specifies fitting method, bounds, and start points.
Options for All Fitting Methods
Option to center and scale the data, specified as the comma-separated pair consisting of 'Normalize' and 'on' or 'off'.
Data Types: char
Points to exclude from the fit, specified as the comma-separated pair consisting of
'Exclude' and one of:
An expression describing a logical vector, e.g.,
x > 10.A vector of integers indexing the points you want to exclude, e.g.,
[1 10 25].A logical vector for all data points where
truerepresents an outlier, created byexcludedata.
For an example, see Exclude Points and Plot Fit Showing Excluded Data.
Data Types: logical | double
Values to assign to the problem-dependent constants, specified as the comma-separated pair consisting of 'problem' and a cell array with one element per problem dependent constant. For details, see fittype.
Data Types: cell | double
Smoothing Options
Smoothing parameter, specified as the comma-separated pair consisting of 'SmoothingParam' and a scalar value between 0 and 1. The default value depends on the data set. Only available if the fit type is smoothingspline.
Data Types: double
Proportion of data points to use in local regressions, specified as the comma-separated pair consisting of 'Span' and a scalar value between 0 and 1. Only available if the fit type is lowess or loess.
Data Types: double
Interpolation Options
Extrapolation method for an interpolant fit, specified as one of the following values.
| Value | Description | Supported Fits |
|---|---|---|
"auto" | Default value for all interpolant fit types. Set | All interpolant fit types and |
"none" | No extrapolation. Query points outside of the convex hull of the fitting data evaluate to | Curve fits — Surface fits — Curve and surface fits — |
"linear" | Linear extrapolation based on boundary gradients. | Surface fits — Curve and surface fits — |
"nearest" | Nearest neighbor extrapolation. This method evaluates to the value of the nearest point on the boundary of the fitting data's convex hull.
| Curve fits — Surface fits — Curve and surface fits — |
"thinplate" | Thin-plate spline extrapolation. This method extends the thin-plate interpolating spline outside of the fitting data's convex hull. For more information, see | Surface fits — |
"biharmonic" | Biharmonic spline extrapolation. This method extends the biharmonic interpolating spline outside of the fitting data's convex hull. | Surface fits — |
"pchip" | Piecewise cubic hermite interpolating polynomial (PCHIP) extrapolation. This method extends a shape-preserving PCHIP outside of the fitting data's convex hull. For more information, see | Curve fits — |
"cubic" | Cubic spline extrapolation. This method extends a cubic interpolating spline outside of the fitting data's convex hull.
| Curve fits — |
Data Types: char | string
Linear and Nonlinear Least-Squares Options
Robust linear least-squares fitting method, specified as the comma-separated pair consisting of 'Robust' and one of these values:
'LAR'specifies the least absolute residual method.'Bisquare'specifies the bisquare weights method.
Available when the fit type Method is LinearLeastSquares or NonlinearLeastSquares.
Data Types: char
Lower bounds on the coefficients to be fitted, specified as the comma-separated pair consisting of 'Lower' and a vector. The default value is an empty vector, indicating that the fit is unconstrained by lower bounds. If bounds are specified, the vector length must equal the number of coefficients. Find the order of the entries for coefficients in the vector value by using the coeffnames function. For an example, see Find Coefficient Order to Set Start Points and Bounds. Individual unconstrained lower bounds can be specified by -Inf.
Available when the Method is LinearLeastSquares or NonlinearLeastSquares.
Data Types: double
Upper bounds on the coefficients to be fitted, specified as the comma-separated pair consisting of 'Upper' and a vector. The default value is an empty vector, indicating that the fit is unconstrained by upper bounds. If bounds are specified, the vector length must equal the number of coefficients. Find the order of the entries for coefficients in the vector value by using the coeffnames function. For an example, see Find Coefficient Order to Set Start Points and Bounds. Individual unconstrained upper bounds can be specified by +Inf.
Available when the Method is LinearLeastSquares or NonlinearLeastSquares.
Data Types: logical
Since R2025a
Points to fit through, specified as a n-by-2 numeric
matrix for curves and n-by-3 numeric matrix for
surfaces. Each row represents one constraint point and each column represents the
x,y or z coordinate for the
point. The number of constraint points cannot be greater than the number of coefficients
in the specified fitType. You can find the number of coefficients
in the fittype using numcoeffs. Specifying the maximum
number of constraint points results in only one solution, with the resulting solution
independent of the input data.
Note
You must have Optimization Toolbox™ installed to use constraint points for fitting a model.
Available when the Method is LinearLeastSquares
or NonlinearLeastSquares.
Example: [0 0; 1 5]
Data Types: double
Since R2025a
Tolerance for constraint points, specified as a nonnegative numeric scalar. This is the upper bound of the absolute numerical difference between the provided constraint point and the actual point the fit passes through, before a constraint violation occurs.
If ConstraintPoints name-value argument is not specified,
TolCon has no effect.
Note
TolCon operates differently from other tolerances. If
TolCon is satisfied, the solver still continues, unless it
is halted for another reason. A solver does not halt simply because
TolCon is satisfied.
Available when the Method is LinearLeastSquares
or NonlinearLeastSquares.
Data Types: double
Nonlinear Least-Squares Options
Initial values for the coefficients, specified as the comma-separated pair consisting of 'StartPoint' and a vector. Find the order of the entries for coefficients in the vector value by using the coeffnames function. For an example, see Find Coefficient Order to Set Start Points and Bounds.
If no start points (the default value of an empty vector) are passed to the fit function, starting points for some library models are determined heuristically. For rational and Weibull models, and all custom nonlinear models, the toolbox selects default initial values for coefficients uniformly at random from the interval (0,1). As a result, multiple fits using the same data and model might lead to different fitted coefficients. To avoid this, specify initial values for coefficients with a fitoptions object or a vector value for the StartPoint value.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Algorithm to use for the
fitting procedure, specified as "Levenberg-Marquardt",
"Trust-Region" or "Interior-Point". The
algorithm must be "Interior-Point" when
ConstraintPoints are provided. If another algorithm is
specified, the software will switch the algorithm to
"Interior-Point". The Optimization Toolbox is required to use the Interior-Point algorithm.
Available when the Method is
NonlinearLeastSquares.
Data Types: char
Maximum change in coefficients for finite difference gradients, specified as the comma-separated pair consisting of 'DiffMaxChange' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Minimum change in coefficients for finite difference gradients, specified as the comma-separated pair consisting of 'DiffMinChange' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Display option in the command window, specified as the comma-separated pair consisting of 'Display' and one of these options:
'notify'displays output only if the fit does not converge.'final'displays only the final output.'iter'displays output at each iteration.'off'displays no output.
Available when the Method is NonlinearLeastSquares.
Data Types: char
Maximum number of evaluations of the model allowed, specified as the comma-separated pair consisting of 'MaxFunEvals' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Maximum number of iterations allowed for the fit, specified as the comma-separated pair consisting of 'MaxIter' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Termination tolerance on the model value, specified as the comma-separated pair consisting of 'TolFun' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Termination tolerance on the coefficient values, specified as the comma-separated pair consisting of 'TolX' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Output Arguments
Fit result, returned as a cfit (for curves) or sfit (for surfaces) object. See Fit Postprocessing for functions for plotting, evaluating, calculating confidence intervals, integrating, differentiating, or modifying your fit object.
Goodness-of-fit statistics, returned as the gof structure including the fields in this table.
Field | Value |
|---|---|
| Sum of squares due to error |
| R-squared (coefficient of determination) |
| Degrees of freedom in the error |
| Degree-of-freedom adjusted coefficient of determination |
| Root mean squared error (standard error) |
Example: gof.rmse
Fitting algorithm information, returned as the output structure containing information associated with the fitting algorithm.
Fields depend on the algorithm. For example, the output structure for nonlinear least-squares algorithms includes the fields shown in this table.
Field | Value |
|---|---|
| Number of observations (response values) |
| Number of unknown parameters (coefficients) to fit |
| Vector of raw residuals (observed values minus the fitted values) |
| Jacobian matrix |
| Describes the exit condition of the algorithm. Positive flags indicate convergence, within tolerances. Zero flags indicate that the maximum number of function evaluations or iterations was exceeded. Negative flags indicate that the algorithm did not converge to a solution. |
| Number of iterations |
| Number of function evaluations |
| Measure of first-order optimality (absolute maximum of gradient components) |
| Fitting algorithm employed |
| Exit message |
Example: output.Jacobian
Version History
Introduced before R2006aFor regression fittypes, you can specify fixed points to fit the curve or surface through
by using the new ConstraintPoints name-value argument. You can also
provide the constraint tolerance using the new TolCon name-value
argument. The software fits the curve of surface through the constraint point using the new
"Interior-Point" algorithm.
Note
You must have Optimization Toolbox installed to use constraint points for fitting a model.
For nonlinear regression models, you can specify a new
"Interior-Point" algorithm for the fitting procedure using
the Algorithm name-value argument. The Optimization Toolbox is required to use the Interior-Point algorithm.
Starting in R2024a, you can create natural neighbor interpolant surface fits. For more information, see List of Library Models for Curve and Surface Fitting.
Starting in R2023b, you can specify additional extrapolation methods for interpolant curve
fits by using the ExtrapolationMethod name-value argument. For
more information, see Extrapolation for Interpolant Fit Types.
Starting in R2023b, you can specify sigmoidal and logarithmic fit types for curve fits. For more information, see List of Library Models for Curve and Surface Fitting.
Starting in R2023a, you can specify the extrapolation method for interpolant fits by using the
ExtrapolationMethod name-value argument. For curve fits,
Curve Fitting Toolbox™ supports only the default extrapolation methods available in previous
releases.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)