Using FEEDBACK to Close Feedback Loops
This example shows why you should always use FEEDBACK to close feedback loops.
Two Ways of Closing Feedback Loops
Consider the following feedback loop
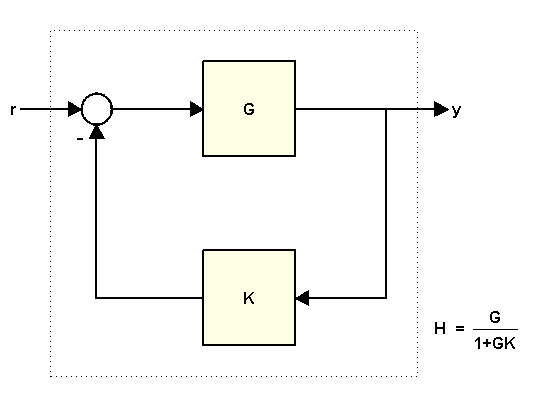
where
K = 2; G = tf([1 2],[1 .5 3])
G =
s + 2
---------------
s^2 + 0.5 s + 3
Continuous-time transfer function.
Model Properties
You can compute the closed-loop transfer function H from r to y in at least two ways:
Using the
feedbackcommandUsing the formula
To compute H using feedback, type
H = feedback(G,K)
H =
s + 2
---------------
s^2 + 2.5 s + 7
Continuous-time transfer function.
Model Properties
To compute H from the formula, type
H2 = G/(1+G*K)
H2 =
s^3 + 2.5 s^2 + 4 s + 6
-----------------------------------
s^4 + 3 s^3 + 11.25 s^2 + 11 s + 21
Continuous-time transfer function.
Model Properties
Why Using FEEDBACK is Better
A major issue with computing H from the formula is that it inflates the order of the closed-loop transfer function. In the example above, H2 has double the order of H. This is because the expression G/(1+G*K) is evaluated as a ratio of the two transfer functions G and 1+G*K. If
then G/(1+G*K) is evaluated as:
As a result, the poles of G are added to both the numerator and denominator of H. You can confirm this by looking at the ZPK representation:
zpk(H2)
ans =
(s+2) (s^2 + 0.5s + 3)
---------------------------------
(s^2 + 0.5s + 3) (s^2 + 2.5s + 7)
Continuous-time zero/pole/gain model.
Model Properties
This excess of poles and zeros can negatively impact the accuracy of your results when dealing with high-order transfer functions, as shown in the next example. This example involves a 17th-order transfer function G. As you did before, use both approaches to compute the closed-loop transfer function for K=1:
load numdemo G H1 = feedback(G,1); % good H2 = G/(1+G); % bad
To have a point of reference, also compute an FRD model containing the frequency response of G and apply feedback to the frequency response data directly:
w = logspace(2,5.1,100); H0 = feedback(frd(G,w),1);
Then compare the magnitudes of the closed-loop responses:
sigmaplot(H0,'b',H1,'g--',H2,'r'); legend('Reference H0','H1=feedback(G,1)','H2=G/(1+G)','location','southwest'); ylim([-60 0])
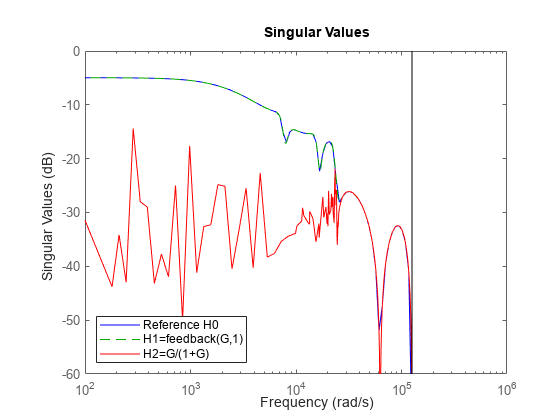
The frequency response of H2 is inaccurate for frequencies below 2e4 rad/s. This inaccuracy can be traced to the additional (cancelling) dynamics introduced near z=1. Specifically, H2 has about twice as many poles and zeros near z=1 as H1. As a result, H2(z) has much poorer accuracy near z=1, which distorts the response at low frequencies. See the example Using the Right Model Representation for more details.