MIMO Feedback Loop
This example shows how to obtain the closed-loop response of a MIMO feedback loop in three different ways.
In this example, you obtain the response from Azref to Az of the MIMO feedback loop of the following block diagram.

You can compute the closed-loop response using one of the following three approaches:
Name-based interconnection with
connectName-based interconnection with
feedbackIndex-based interconnection with
feedback
You can use whichever of these approaches is most convenient for your application.
Load the plant Aerodyn and the controller Autopilot into the MATLAB® workspace. These models are stored in the datafile MIMOfeedback.mat.
load('MIMOfeedback.mat')Aerodyn is a 4-input, 7-output state-space (ss) model. Autopilot is a 5-input, 1-output ss model. The inputs and outputs of both models names appear as shown in the block diagram.
Compute the closed-loop response from Azref to Az using connect.
T1 = connect(Autopilot,Aerodyn,'Azref','Az');
Warning: The following block inputs are not used: Rho,a,Thrust.
Warning: The following block outputs are not used: Xe,Ze,Altitude.
The connect function combines the models by joining the inputs and outputs that have matching names. The last two arguments to connect specify the input and output signals of the resulting model. Therefore, T1 is a state-space model with input Azref and output Az. The connect function ignores the other inputs and outputs in Autopilot and Aerodyn.
Compute the closed-loop response from Azref to Az using name-based interconnection with the feedback command. Use the model input and output names to specify the interconnections between Aerodyn and Autopilot.
When you use the feedback function, think of the closed-loop system as a feedback interconnection between an open-loop plant-controller combination L and a diagonal unity-gain feedback element K. The following block diagram shows this interconnection.
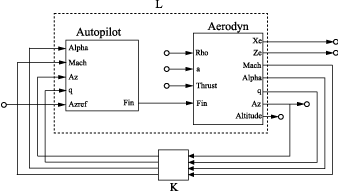
L = series(Autopilot,Aerodyn,'Fin'); FeedbackChannels = {'Alpha','Mach','Az','q'}; K = ss(eye(4),'InputName',FeedbackChannels,... 'OutputName',FeedbackChannels); T2 = feedback(L,K,'name',+1);
The closed-loop model T2 represents the positive feedback interconnection of L and K. The 'name' option causes feedback to connect L and K by matching their input and output names.
T2 is a 5-input, 7-output state-space model. The closed-loop response from Azref to Az is T2('Az','Azref').
Compute the closed-loop response from Azref to Az using feedback, using indices to specify the interconnections between Aerodyn and Autopilot.
L = series(Autopilot,Aerodyn,1,4); K = ss(eye(4)); T3 = feedback(L,K,[1 2 3 4],[4 3 6 5],+1);
The vectors [1 2 3 4] and [4 3 6 5] specify which inputs and outputs, respectively, complete the feedback interconnection. For example, feedback uses output 4 and input 1 of L to create the first feedback interconnection. The function uses output 3 and input 2 to create the second interconnection, and so on.
T3 is a 5-input, 7-output state-space model. The closed-loop response from Azref to Az is T3(6,5).
Compare the step response from Azref to Az to confirm that the three approaches yield the same results.
step(T1,T2('Az','Azref'),T3(6,5),2)
