F-OFDM vs. OFDM Modulation
This example compares Orthogonal Frequency Division Multiplexing (OFDM) with Filtered-OFDM (F-OFDM) and highlights the merits of the candidate modulation scheme for Fifth Generation (5G) communication systems.
Introduction
This example compares Filtered-OFDM modulation with generic Cyclic Prefix OFDM (CP-OFDM) modulation. For F-OFDM, a well-designed filter is applied to the time domain OFDM symbol to improve the out-of-band radiation of the sub-band signal, while maintaining the complex-domain orthogonality of OFDM symbols.
This example models Filtered-OFDM modulation with configurable parameters. It highlights the filter design technique and the basic transmit/receive processing.
s = rng('default'); % Set RNG state for repeatability
System Parameters
Define system parameters for the example. These parameters can be modified to explore their impact on the system.
numFFT = 1024; % Number of FFT points numRBs = 50; % Number of resource blocks rbSize = 12; % Number of subcarriers per resource block cpLen = 72; % Cyclic prefix length in samples bitsPerSubCarrier = 6; % 2: QPSK, 4: 16QAM, 6: 64QAM, 8: 256QAM snrdB = 18; % SNR in dB toneOffset = 2.5; % Tone offset or excess bandwidth (in subcarriers) L = 513; % Filter length (=filterOrder+1), odd
Filtered-OFDM Filter Design
Appropriate filtering for F-OFDM satisfies the following criteria:
Should have a flat passband over the subcarriers in the sub-band
Should have a sharp transition band to minimize guard-bands
Should have sufficient stop-band attenuation
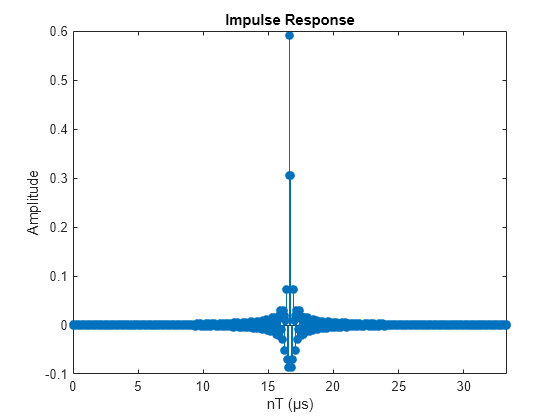
A filter with a rectangular frequency response, i.e. a sinc impulse response, meets these criteria. To make this causal, the low-pass filter is realized using a window, which, effectively truncates the impulse response and offers smooth transitions to zero on both ends [ 3 ].
numDataCarriers = numRBs*rbSize; % number of data subcarriers in sub-band halfFilt = floor(L/2); n = -halfFilt:halfFilt; % Sinc function prototype filter pb = sinc((numDataCarriers+2*toneOffset).*n./numFFT); % Sinc truncation window w = (0.5*(1+cos(2*pi.*n/(L-1)))).^0.6; % Normalized lowpass filter coefficients fnum = (pb.*w)/sum(pb.*w); % Filter impulse response impz(fnum,1,[],15.36e6)
% Use dsp filter objects for filtering filtTx = dsp.FIRFilter(Structure='Direct form symmetric', ... Numerator=fnum); filtRx = clone(filtTx); % Matched filter for the Rx
F-OFDM Transmit Processing
In F-OFDM, the sub-band CP-OFDM signal is passed through the designed filter. As the filter's passband corresponds to the signal's bandwidth, only the few subcarriers close to the edge are affected. A key consideration is that the filter length can be allowed to exceed the cyclic prefix length for F-OFDM [ 1 ]. The inter-symbol interference incurred is minimized due to the filter design using windowing (with soft truncation).
Transmit-end processing operations are shown in the following F-OFDM transmitter diagram.

% Set up a figure for spectrum plot hFig = figure(Position=figposition([46 50 30 30]), MenuBar='none'); axis([-0.5 0.5 -200 -20]); hold on; grid on xlabel('Normalized frequency'); ylabel('PSD (dBW/Hz)') title(['F-OFDM, ' num2str(numRBs) ' Resource blocks, ' ... num2str(rbSize) ' Subcarriers each']) % Generate data symbols bitsIn = randi([0 1], bitsPerSubCarrier*numDataCarriers, 1); % QAM Symbol mapper symbolsIn = qammod(bitsIn, 2^bitsPerSubCarrier,InputType='bit', ... UnitAveragePower=true); % Pack data into an OFDM symbol offset = (numFFT-numDataCarriers)/2; % for band center symbolsInOFDM = [zeros(offset,1); symbolsIn; ... zeros(numFFT-offset-numDataCarriers,1)]; ifftOut = ifft(ifftshift(symbolsInOFDM)); % Prepend cyclic prefix txSigOFDM = [ifftOut(end-cpLen+1:end); ifftOut]; % Filter, with zero-padding to flush tail. Get the transmit signal txSigFOFDM = filtTx([txSigOFDM; zeros(L-1,1)]); % Plot power spectral density (PSD) [psd,f] = periodogram(txSigFOFDM, rectwin(length(txSigFOFDM)), ... numFFT*2, 1, 'centered'); plot(f,10*log10(psd));

% Compute peak-to-average-power ratio (PAPR) pm = powermeter(Measurement="Peak-to-average power ratio",ComputeCCDF=true); paprFOFDM = pm(txSigFOFDM); disp(['Peak-to-Average-Power-Ratio for F-OFDM = ' num2str(paprFOFDM) ' dB']);
Peak-to-Average-Power-Ratio for F-OFDM = 9.8642 dB
OFDM Modulation with Corresponding Parameters
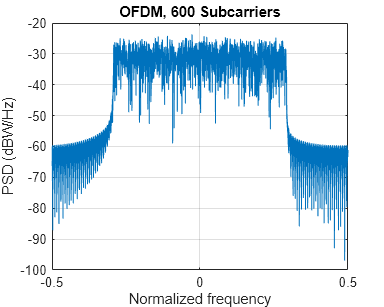
For comparison, we review the existing OFDM modulation technique, using the full occupied band, with the same length cyclic prefix.
% Plot power spectral density (PSD) for OFDM signal [psd,f] = periodogram(txSigOFDM, rectwin(length(txSigOFDM)), numFFT*2, ... 1, 'centered'); hFig1 = figure('Position', figposition([46 15 30 30])); plot(f,10*log10(psd)); grid on axis([-0.5 0.5 -100 -20]); xlabel('Normalized frequency'); ylabel('PSD (dBW/Hz)') title(['OFDM, ' num2str(numRBs*rbSize) ' Subcarriers'])
% Compute peak-to-average-power ratio (PAPR) pm = powermeter(Measurement="Peak-to-average power ratio",ComputeCCDF=true); paprOFDM = pm(txSigOFDM); disp(['Peak-to-Average-Power-Ratio for OFDM = ' num2str(paprOFDM) ' dB']);
Peak-to-Average-Power-Ratio for OFDM = 8.1879 dB
Comparing the plots of the spectral densities for CP-OFDM and F-OFDM schemes, F-OFDM has lower side lobes. This allows a higher utilization of the allocated spectrum, leading to increased spectral efficiency.
Refer to the comm.OFDMModulator System object™ which can also be used to implement the CP-OFDM modulation.
F-OFDM Receiver with No Channel
The example next highlights the basic receive processing for F-OFDM for a single OFDM symbol. The received signal is passed through a matched filter, followed by the normal CP-OFDM receiver. It accounts for both the filtering ramp-up and latency prior to the FFT operation.
No fading channel is considered in this example but noise is added to the received signal to achieve the desired SNR.
% Add WGN rxSig = awgn(txSigFOFDM, snrdB, 'measured');
Receive processing operations are shown in the following F-OFDM receiver diagram.

% Receive matched filter rxSigFilt = filtRx(rxSig); % Account for filter delay rxSigFiltSync = rxSigFilt(L:end); % Remove cyclic prefix rxSymbol = rxSigFiltSync(cpLen+1:end); % Perform FFT RxSymbols = fftshift(fft(rxSymbol)); % Select data subcarriers dataRxSymbols = RxSymbols(offset+(1:numDataCarriers)); % Plot received symbols constellation switch bitsPerSubCarrier case 2 % QPSK refConst = qammod((0:3).', 4, UnitAveragePower=true); case 4 % 16QAM refConst = qammod((0:15).', 16,UnitAveragePower=true); case 6 % 64QAM refConst = qammod((0:63).', 64,UnitAveragePower=true); case 8 % 256QAM refConst = qammod((0:255).', 256,UnitAveragePower=true); end constDiagRx = comm.ConstellationDiagram( ... ShowReferenceConstellation=true, ... ReferenceConstellation=refConst, ... Position=figposition([20 15 30 40]), ... EnableMeasurements=true, ... MeasurementInterval=length(dataRxSymbols), ... Title='F-OFDM Demodulated Symbols', ... Name='F-OFDM Reception', ... AxesLimits=[-1.5 1.5]); constDiagRx(dataRxSymbols);
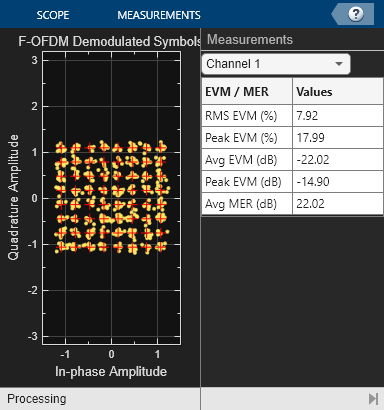
% Channel equalization is not necessary here as no channel is modeled % BER computation BER = comm.ErrorRate; % Perform hard decision and measure errors rxBits = qamdemod(dataRxSymbols, 2^bitsPerSubCarrier,OutputType='bit', ... UnitAveragePower=true); ber = BER(bitsIn, rxBits); disp(['F-OFDM Reception, BER = ' num2str(ber(1)) ' at SNR = ' ... num2str(snrdB) ' dB']);
F-OFDM Reception, BER = 0.0013889 at SNR = 18 dB
% Restore RNG state
rng(s);As highlighted, F-OFDM adds a filtering stage to the existing CP-OFDM processing at both the transmit and receive ends. The example models the full-band allocation for a user, but the same approach can be applied for multiple bands (one per user) for an uplink asynchronous operation.
Refer to the comm.OFDMDemodulator System object™ which can be used to implement the CP-OFDM demodulation after receive matched filtering.
Conclusion and Further Exploration
The example presents the basic characteristics of the F-OFDM modulation scheme at both transmit and receive ends of a communication system. Explore different system parameter values for the number of resource blocks, number of subcarriers per blocks, filter length, tone offset and SNR.
Universal Filtered Multi-Carrier (UFMC) modulation scheme is another approach to sub-band filtered OFDM. For more information, see the UFMC vs. OFDM Modulation example. This F-OFDM example uses a single sub-band while the UFMC example uses multiple sub-bands.
F-OFDM and UFMC both use time-domain filtering with subtle differences in the way the filter is designed and applied. For UFMC, the length of filter is constrained to be equal to the cyclic-prefix length, while for F-OFDM, it can exceed the CP length.
For F-OFDM, the filter design leads to a slight loss in orthogonality (strictly speaking) which affects only the edge subcarriers.
Selected Bibliography
Abdoli J., Jia M. and Ma J., "Filtered OFDM: A New Waveform for Future Wireless Systems," 2015 IEEE® 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, 2015, pp. 66-70.
R1-162152. "OFDM based flexible waveform for 5G." 3GPP TSG RAN WG1 meeting 84bis. Huawei; HiSilicon. April 2016.
R1-165425. "F-OFDM scheme and filter design." 3GPP TSG RAN WG1 meeting 85. Huawei; HiSilicon. May 2016.