comm.GoldSequence
Generate Gold sequence from set of sequences
Description
The comm.GoldSequence
System object™ generates a binary sequence with small periodic cross-correlation
properties from a bounded set of sequences. For more information, see Gold Sequences.
To generate a Gold sequence from set of sequences:
Create the
comm.GoldSequenceobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
goldseq = comm.GoldSequence
goldseq = comm.GoldSequence(Name=Value)goldseq =
comm.GoldSequence(Shift=1) specifies a one sample offset of the
output sequence from the starting point.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Generator polynomial for the first preferred PN sequence, specified as one of these options:
Character vector or string scalar of a polynomial whose constant term is
1. For more information, see Representation of Polynomials in Communications Toolbox.Binary-valued row vector that represents the coefficients of the polynomial in order of descending powers. The length of this vector must be N + 1, where N is the degree of the polynomial. The first and last entries must be
1, indicating the leading term with degree N and a constant term of 1.Integer-valued row vector of elements that represent the exponents for the nonzero terms of the polynomial in order of descending powers. The last entry must be
0, indicating a constant term of 1.
This property determines the feedback connections for the shift register
of the first preferred PN sequence generator. The degree of the first
generator polynomial must equal the degree of the second generator
polynomial specified by the SecondPolynomial property. For more information, see Preferred Pairs of Sequences.
Example: 'z^8 + z^2 + 1', [1 0 0 0 0 0 1 0
1], and [8 2 0] represent the same
polynomial, p(z) =
z8 +
z2 +
1.
Data Types: double | char
Initial conditions used for the shift register of the first preferred PN sequence generator when the simulation starts, specified as a binary-valued scalar or binary-valued vector.
If you set this property to a scalar, the initial value of all cells in the shift register are the specified scalar value.
If you set this property to a vector, each element of the vector corresponds to the initial value of the corresponding cell in the shift register. The length of the vector must equal the degree of the generator polynomial specified by the
FirstPolynomialproperty.
Note
For the object to generate a nonzero sequence, at least one element of the initial conditions for the first or second preferred PN sequence generator must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.
Data Types: double
Generator polynomial for the first preferred PN sequence, specified as one of these options:
Character vector or string scalar of a polynomial whose constant term is
1. For more information, see Representation of Polynomials in Communications Toolbox.Binary-valued row vector that represents the coefficients of the polynomial in order of descending powers. The length of this vector must be N + 1, where N is the degree of the polynomial. The first and last entries must be
1, indicating the leading term with degree N and a constant term of 1.Integer-valued row vector of elements that represent the exponents for the nonzero terms of the polynomial in order of descending powers. The last entry must be
0, indicating a constant term of 1.
This property determines the feedback connections for the shift register
of the second preferred PN sequence generator. The degree of the second
generator polynomial must equal the degree of the first generator polynomial
specified by the FirstPolynomial
property. For more information, see Preferred Pairs of Sequences.
Data Types: double | char
Source of the initial conditions used for the shift register of the second preferred PN sequence generator, specified as one of these values:
'Property'— Specify PN sequence generator initial conditions by using theSecondInitialConditionsproperty.'Input port'— Specify PN sequence generator initial conditions by using thesecondinitcondinput argument.
Data Types: string | char
Initial conditions used for the shift register of the second preferred PN sequence generator when the simulation starts, specified as a binary-valued scalar or binary-valued vector.
If you set this property to a scalar, the initial value of all cells in the shift register are the specified scalar value.
If you set this property to a vector, each element of the vector corresponds to the initial value of the corresponding cell in the shift register. The length of the vector must equal the degree of the generator polynomial specified by the
SecondPolynomialproperty.
Note
For the object to generate a nonzero sequence, at least one element of the initial conditions for the first or second preferred PN sequence generator must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.
Dependencies
To enable this property set the SecondInitialConditionsSource property to
'Property'.
Data Types: double
Sequence index of the output sequence from the set of Gold sequences, specified as an integer in the range [–2, 2n–2]. n is the degree of the preferred polynomials. For more information, see Sequence Index and Gold Sequences.
Data Types: double
Offset of the output sequence from the starting point, specified as an integer. Units are in samples. The object wraps shift values that are negative or greater than the length of the Gold sequence. For an example using shift, see Generate Gold Sequences with Various Shift Values.
Note
Calculate the mask vector by using the shift2mask function.
Data Types: double
Enable variable-size outputs, specified as a numeric or logical
0 (false) or 1
(true). To enable variable-size outputs by using the
outputsize input argument, set this property to
true. The enabled input specifies the output size of
the Gold sequence. The input value must be less than or equal to the value
of the MaximumOutputSize property.
When you set this property to false, the SamplesPerFrame
property specifies the number of output samples.
Data Types: logical | double
Maximum output frame size, specified as a vector of the form
[m 1], where m is a positive
integer. The first element of the vector indicates the maximum length of the
output frame and the second element of the vector must be
1.
Example: [20 1] specifies a maximum frame output size of
20-by-1.
Dependencies
To enable this property, set the VariableSizeOutput property to
true.
Data Types: double
Number of samples output per frame, specified as a positive integer. If
you set this property to a value of M, the object outputs
M samples of a Gold sequence that has a period of N =
2n –
1, where n is the degree of the generator
polynomials specified by the FirstPolynomial
and SecondPolynomial properties.
Dependencies
To enable this property, set the VariableSizeOutput property to
false.
Data Types: double
Enable the generator reset input, specified as a numeric or logical
0 (false) or 1
(true). To enable the ability to reset the sequence
generator using the resetseq input argument, set this property to
true. This input resets the states of the two shift
registers of the Gold sequence generator to the initial conditions specified
by the FirstInitialConditions and SecondInitialConditions properties. For an example using the
resetseq input, see Generate Gold Sequences with Various Reset Values.
Dependencies
To enable this property, set the SecondInitialConditionsSource property to
'Property'.
Data Types: logical | double
Data type of the output, specified as 'double',
'logical', or 'Smallest unsigned
integer'.
To use the Smallest unsigned integer option, you must
have the Fixed-Point Designer™ product.
Data Types: string | char
Usage
Syntax
Description
outSequence = goldseq()
outSequence = goldseq(secondinitcond)secondinitcond as the initial conditions for the
second PN sequence.
To enable this syntax, set the SecondInitialConditionsSource property to 'Input
port' and the ResetInputPort
property to false.
outSequence = goldseq(outputsize)outputsize as the output size.
To enable this syntax, set the VariableSizeOutput property to true.
outSequence = goldseq(resetseq)resetseq as the reset signal.
To enable this syntax, set the ResetInputPort
property to true and the SecondInitialConditionsSource property to
'Property'.
outSequence = goldseq(secondinitcond,outputsize)
To enable this syntax, set the SecondInitialConditionsSource property to 'Input
port', the ResetInputPort
property to false, and set the VariableSizeOutput property to true.
outSequence = goldseq(outputsize,resetseq)
To enable this syntax, set the VariableSizeOutput property to true, the
SecondInitialConditionsSource property to
'Property', and the ResetInputPort
property to true.
Input Arguments
Initial conditions used for the shift register of the second preferred PN sequence generator when the simulation starts, specified as a binary-valued scalar or binary-valued vector.
If you set this input to a scalar, the initial value of all cells in the shift register are the specified scalar value.
If you set this input to a vector, each element of the vector corresponds to the initial value of the corresponding cell in the shift register. The length of the vector must equal the degree of the generator polynomial specified by the
SecondPolynomialproperty.
Note
For the object to generate a nonzero sequence, at least one element of the initial conditions for the first or second preferred PN sequence generator must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.
This object accepts variable-size inputs. After the object is locked, you can change the size of each input channel, but you cannot change the number of channels. For more information, see Variable-Size Signal Support with System Objects.
Dependencies
To enable this input argument, set the SecondInitialConditionsSource property to
'Input port'.
Data Types: double
Length of the output sequence, specified as a nonnegative integer,
n, or a vector of the form [n
1], where n is a positive integer. The first element
of the vector indicates the length of the output frame and the second
element of the vector must be 1.
The scalar or the first element of the row vector must be less than or
equal to the first element of the MaximumOutputSize property value.
Dependencies
To enable this input argument, set the VariableSizeOutput property to
true.
Data Types: double
Reset sequence generator, specified as a scalar or a column vector
with length equal to the number of samples per frame specified by the
SamplesPerFrame property.
When you specify this input as a nonzero scalar, the object resets to the specified initial conditions and then generates a new output frame.
When you specify this input as a column vector, the object resets to the specified initial conditions at each sample in the output frame that aligns with a nonzero value in the reset vector.
For an example using reset, see Generate Gold Sequences with Various Reset Values.
Dependencies
To enable this input argument, set the ResetInputPort property to
true.
Data Types: double | logical
Output Arguments
Gold sequence, returned as a column vector. For more information, see Gold Sequences.
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Generate 10 samples of a Gold sequence with a period of .
goldseq = comm.GoldSequence('FirstPolynomial','x^5+x^2+1', ... 'SecondPolynomial','x^5+x^4+x^3+x^2+1', ... 'FirstInitialConditions',[0 0 0 0 1], ... 'SecondInitialConditions',[0 0 0 0 1], ... 'Index',4,'SamplesPerFrame',10); x = goldseq()
x = 10×1
1
1
1
0
0
0
0
0
0
1
Generate Gold sequences using different values for the shift input to demonstrate that the object wraps shift values that are negative or greater than the sequence length.
Create a Gold sequence System object™, specifying 15 samples per frame and no shift. Generate the 7-sample Gold sequence. The output frame begins at the start of the Gold sequence.
goldseq = comm.GoldSequence( ... "FirstPolynomial","x^3+x^2+1", ... "SecondPolynomial","x^3+x+1", ... "FirstInitialConditions",[0 0 1], ... "SecondInitialConditions",[0 1 1], ... "Index",3, ... "SamplesPerFrame",15)
goldseq =
comm.GoldSequence with properties:
FirstPolynomial: "x^3+x^2+1"
FirstInitialConditions: [0 0 1]
SecondPolynomial: "x^3+x+1"
SecondInitialConditionsSource: 'Property'
SecondInitialConditions: [0 1 1]
Index: 3
Shift: 0
VariableSizeOutput: false
SamplesPerFrame: 15
ResetInputPort: false
OutputDataType: 'double'
outseq = goldseq()'
outseq = 1×15
1 1 0 0 0 0 0 1 1 0 0 0 0 0 1
Release the object, adjust the shift to -1, and generate the shifted output. Repeat this process for shift values of 6 and 13. For each of these shift settings, the output frame begins at the 6th sample of this 7-sample long Gold sequence.
release(goldseq); goldseq.Shift = -1; outseq = goldseq()'
outseq = 1×15
0 1 1 0 0 0 0 0 1 1 0 0 0 0 0
release(goldseq); goldseq.Shift = 6; outseq = goldseq()'
outseq = 1×15
0 1 1 0 0 0 0 0 1 1 0 0 0 0 0
release(goldseq); goldseq.Shift = 13; outseq = goldseq()'
outseq = 1×15
0 1 1 0 0 0 0 0 1 1 0 0 0 0 0
Generate Gold sequences using different values for the reset input.
Create a Gold sequence System object™, specifying 15 samples per frame and enabling the reset input. Generate the 7-sample Gold sequence. To observe the starting point of frames output by the object relative to the generated Gold sequence, the samples per frame value includes one sample more than two times the sequence length.
goldseq = comm.GoldSequence( ... "FirstPolynomial","x^3+x^2+1", ... "SecondPolynomial","x^3+x+1", ... "FirstInitialConditions",[0 0 1], ... "SecondInitialConditions",[0 1 1], ... "Index",3, ... "ResetInputPort",true, ... "SamplesPerFrame",15);
So that the object does not reset the sequence to the initial conditions, specify a scalar reset input value of 0. Display consecutive 15-sample frames of the sequence. The second frame continues the sequence from where the first frame left off, with the second element of the Gold sequence.
resetseq = 0; x1 = goldseq(resetseq)'
x1 = 1×15
1 1 0 0 0 0 0 1 1 0 0 0 0 0 1
x2 = goldseq(resetseq)'
x2 = 1×15
1 0 0 0 0 0 1 1 0 0 0 0 0 1 1
To reset the sequence to the initial conditions, specify a scalar reset input value of 1. Display consecutive 15-sample frames of the sequence. The second frame now begins with the first element of the Gold sequence.
resetseq = 1; x3 = goldseq(resetseq)'
x3 = 1×15
1 1 0 0 0 0 0 1 1 0 0 0 0 0 1
x4 = goldseq(resetseq)'
x4 = 1×15
1 1 0 0 0 0 0 1 1 0 0 0 0 0 1
To reconfigure the reset input of the object to accept a vector, release the object. Specify a reset input vector filled with 0s. Display consecutive 15-sample frames of the sequence. Since the object does not reset the sequence to the initial conditions, the second frame begins with the second element of the Gold sequence.
release(goldseq) resetseq = [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]'; x5 = goldseq(resetseq)'
x5 = 1×15
1 1 0 0 0 0 0 1 1 0 0 0 0 0 1
x6 = goldseq(resetseq)'
x6 = 1×15
1 0 0 0 0 0 1 1 0 0 0 0 0 1 1
Specify a reset input vector that has two elements with nonzero values. Display consecutive 15-sample frames of the sequence. The second and third frames continue the sequence from the prior frame but reset the sequence at the third and ninth samples of the frame due to the position of the nonzero entries in the vector specified for the reset input.
resetseq = [0 0 1 0 0 0 0 0 1 0 0 0 0 0 0]'; x7 = goldseq(resetseq)'
x7 = 1×15
0 0 1 1 0 0 0 0 1 1 0 0 0 0 0
x8 = goldseq(resetseq)'
x8 = 1×15
1 1 1 1 0 0 0 0 1 1 0 0 0 0 0
x9 = goldseq(resetseq)'
x9 = 1×15
1 1 1 1 0 0 0 0 1 1 0 0 0 0 0
More About
The characteristic cross-correlation properties of Gold sequences
make them useful when multiple devices are broadcasting in the same frequency range.
The Gold sequences are defined using a specified pair of sequences,
u and v, called a preferred pair, as
defined in Preferred Pairs of Sequences. The
u and v pair of sequences has a period
N = 2n – 1,
where n is the degree of the generator polynomials specified by
the FirstPolynomial and
SecondPolynomial
properties. The set G(u, v)
of Gold sequences is defined by
T represents the operator that shifts vectors cyclically to the left by one place, and represents addition modulo 2. G(u,v) contains N + 2 sequences of period N.
Gold sequences have the property that the cross-correlation between any two sequences or between shifted versions of the sequences takes on one of three values: –t(n), –1, or t(n) – 2, where
The object uses two PN sequence generators to generate a preferred pair of sequences. The object then XORs these sequences to produce the output Gold sequence, as shown in this figure.
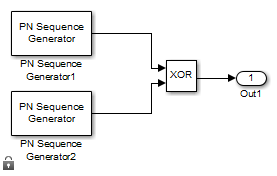
The FirstPolynomial and
SecondPolynomial
properties determine the preferred pair of sequences and the feedback connections
for the shift registers used by the PN sequence generators to generate their output.
For more details on PN sequence generation, see the Simple Shift Register Generator section on the
comm.PNSequence
System object reference page.
This table provides examples of preferred pairs.
| Degree of Generator Polynomials (n) | Pair of Sequences Period (N) | FirstPolynomial Property Value | SecondPolynomial Property Value |
|---|---|---|---|
| 5 | 31 |
[5 2 0]
|
[5 4 3 2 0]
|
| 6 | 63 |
[6 1 0]
|
[6 5 2 1 0]
|
| 7 | 127 |
[7 3 0]
|
[7 3 2 1 0]
|
| 9 | 511 |
[9 4 0]
|
[9 6 4 3 0]
|
| 10 | 1023 |
[10 3 0]
|
[10 8 3 2 0]
|
| 11 | 2047 |
[11 2 0]
|
[11 8 5 2 0]
|
The FirstInitialConditions property and SecondInitialConditions property (or secondinitcond input argument) are values that specify the initial
values of the shift registers corresponding to FirstPolynomial and
SecondPolynomial,
respectively.
Note
For the object to generate a nonzero sequence, at least one element of one of the initial conditions vectors must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.
You can offset the starting point of the Gold sequence by setting the Shift property to a nonzero
value. For an example that adjusts the shift setting, see Generate Gold Sequences with Various Shift Values.
Preferred pairs of sequences, u and v, comprise the set of Gold sequences G(u, v).
For a pair of sequences, u and v, of period N = 2n–1 to be a preferred pair, they must satisfy these requirements:
n is the degree of the generator polynomials specified by the
FirstPolynomialandSecondPolynomialproperties.n is not divisible by
4.v = u[q], where
q is odd.
q = 2k+1 or q = 22k–2k+1.
v is obtained by sampling every qth symbol of u.
For more details on PN sequence generation, see the Simple Shift Register Generator section on the
comm.PNSequence
System object reference page.
The sequence index specified by the Index property specifies which
Gold sequence in the set G(u,
v) is output.
The set of available Gold sequences is
u and v are the two preferred PN sequences, T is the operator that shifts vectors cyclically to the left by one place, and represents addition modulo 2. G(u,v) contains N+2 Gold sequences of period N = 2n–1.
The range of Index is [–2,
2n–2], where
n is the degree of the generator polynomials specified by the
FirstPolynomial and
SecondPolynomial
properties. The index values -2 and -1
correspond to the first and second preferred PN sequences as generated by FirstPolynomial and SecondPolynomial, respectively. This table shows the correspondence
between the sequence index and the output sequence.
Index Property Value | Output Sequence |
|---|---|
–2 | u |
–1 | v |
0 |
|
1 |
|
2 |
|
| ... | ... |
2n
–2
|
|
References
[1] Proakis, John G. Digital Communications. 5th ed. New York: McGraw Hill, 2007.
[2] Gold, R. “Maximal Recursive Sequences with 3-Valued Recursive Cross-Correlation Functions (Corresp.).” IEEE® Transactions on Information Theory 14, no. 1 (January 1968): 154–56. https://doi.org/10.1109/TIT.1968.1054106.
[3] Gold, R. “Optimal Binary Sequences for Spread Spectrum Multiplexing (Corresp.).” IEEE Transactions on Information Theory 13, no. 4 (October 1967): 619–21. https://doi.org/10.1109/TIT.1967.1054048.
[4] Sarwate, D.V., and M.B. Pursley. “Crosscorrelation Properties of Pseudorandom and Related Sequences.” Proceedings of the IEEE 68, no. 5 (1980): 593–619. https://doi.org/10.1109/PROC.1980.11697.
[5] Dixon, Robert C. Spread Spectrum Systems: With Commercial Applications. 3rd ed. New York: Wiley, 1994.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2008a
See Also
Objects
Functions
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)