Carrier Synchronizer
Compensate for carrier frequency offset
Libraries:
Communications Toolbox /
Synchronization
Description
The Carrier Synchronizer block compensates for carrier frequency and phase offsets in signals that use single-carrier modulation schemes. The carrier synchronizer algorithm is compatible with BPSK, QPSK, OQPSK, 8-PSK, PAM, and rectangular QAM modulation schemes.
Note
Modulation-type dependent phase ambiguities may be introduced by the synchronization algorithm. For more information, see Potential Phase Ambiguity.
This icon shows the block without optional port.![]()
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
Algorithms
The algorithm implements a closed-loop compensator that uses the PLL-based algorithm described in [1]. The output of the synchronizer, yn, is a frequency-shifted version of the complex input signal, xn, for the nth sample. The synchronizer output is where λn is the output of the direct digital synthesizer (DDS). The DDS is the discrete-time version of a voltage-controlled oscillator and is a core component of discrete-time phase locked loops. The DDS works as an integration filter.
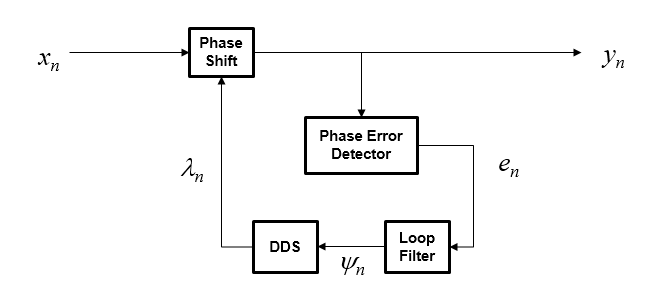
To correct for the frequency offset, first the algorithm determines the phase error, en. The value of the phase error depends on the modulation scheme.
| Modulation | Phase Error |
|---|---|
| QAM or QPSK | For a detailed description of this equation, see [1]. |
| BPSK or PAM | For a detailed description of this equation, see [1]. |
| 8-PSK | For a detailed description of this equation, see [2]. |
| OQPSK |
|
To ensure system stability, the phase error passes through a biquadratic loop filter governed by
where ψn is the output of the loop filter at sample n, and gI is the integrator gain. The integrator gain is determined from the equation
where
Bn is the normalized loop bandwidth
ζ is the damping factor
K0 is the phase recovery gain and equals the number of samples per symbol.
Kp is the phase error detector gain and is determined by the modulation type.
| Modulation | Kp |
|---|---|
| BPSK, PAM, QAM, QPSK, or OQPSK | 2 |
| 8-PSK | 1 |
The output of the loop filter is then passed to the DDS. The DDS is another biquadratic loop filter whose expression is based on the forward Euler integration rule
where gP is the proportional gain that is expressed as
The info object function returns estimates of the
normalized pull-in range, the maximum frequency lock delay, and the maximum phase lock
delay. The normalized pull-in range, (Δf)pull-in, is expressed in radians and estimated as
The expression for (Δf )pull-in becomes less accurate as approaches 1.
The maximum frequency lock delay, TFL, and phase lock delay, TPL, are expressed in samples and estimated as
References
[1] Rice, Michael. Digital Communications: A Discrete-Time Approach. Upper Saddle River, NJ: Prentice Hall, 2008. pp. 359–393.
[2] Huang Zhijie, Yi Zhiqiang, Zhang Ming and Wang Kuang, "8PSK demodulation for new generation DVB-S2," 2004 International Conference on Communications, Circuits and Systems (IEEE Cat. No.04EX914), Chengdu, 2004, pp. 1447-1450 Vol.2, doi: 10.1109/ICCCAS.2004.1346447.
Extended Capabilities
Version History
Introduced in R2015a



