measuredAntenna

Use measured pattern data as exciter for backing structures

Since R2023a

Description

The measuredAntenna object lets you perform port and field analysis on the measured field data of an antenna or array. You can import measured field data from a .txt file, .csv file, or .xlsx file to the MATLAB^® workspace and assign it to the relevant properties of this object. The field data includes Cartesian electric and embedded electric field components in V/m at the observation points, spherical coordinates of the observation points, the phase center, number of excitation ports, measurement frequencies, and S-parameters. The measuredAntenna object also lets you replace the physical exciter of the curved reflector antennas from the antenna catalog with measured field data of the exciter and perform fundamental analysis on the reflector antenna using the Physical Optics solver.

Creation

Syntax

m = measuredAntenna

m = measuredAntenna(PropertyName=Value)

Description

m = measuredAntenna creates an antenna field data object with the x, y, and z-components of the electric field being 0.1 V/m across the observed direction.

example

m = measuredAntenna(PropertyName=Value) creates a measured antenna object, with additional properties using one or more name–value arguments. PropertyName is the property name and Value is the corresponding value. You can specify several name-value arguments in any order as PropertyName1=Value1,...,PropertyNameN=ValueN. Properties that you do not specify, retain their default values.

example

Properties

expand all

`E` — Magnitude of radiated electric field
`[0.1 0.1 0.1]` (default) | `P`-by-3-by-`F` matrix

Cartesian components of the electric field in V/m at observation points, specified as a P-by-3-by-F matrix. P represents the number of observation points and components are specified in [X Y Z] order. The default value is [0.1 0.1 0.1] V/m at a single observation point. F represents the number of frequencies over which the electric field is measured.

Example: E(:,:,1) = [0.5 0.3 0.7]

Example: E(1,:,:) = [0.1 0.1 0.1; 0.2 0.3 0.15;...0.5 0.45 0.35]

Data Types: double
Complex Number Support: Yes

`Direction` — Direction of radiated electric field
`[0 90 100]` (default) | `P`-by-3 matrix

Spherical coordinates of the observation points, specified as a P-by-3 matrix. P represents the number of observation points and the coordinates are specified as [Azimuth(degree) Elevation(degree) Radius(meter)]. The default value is a single observation point at [0 90 100].

Example: [30 60 200]

Example: [0 90 100; ...; 359 359 100]

Data Types: double

`PhaseCenter` — Phase center of measured antenna
`[0 0 0.075]` (default) | 1-by-3 vector

Cartesian coordinates of the phase center of the measured antenna in meter, specified as a 1-by-3 vector in [X Y Z] order. The default phase center is at [0 0 0.075]. Phase center is defined as a point in space from which, when emitted, the far-field phase fronts remain spherical in a certain angular area of interest. PhaseCenter denotes the average phase center of the incident electric field, E.

Example: [0 1 1]

Data Types: double

`NumPorts` — Number of excitation ports
1 (default) | positive scalar integer

Number of excitation ports in the measured antenna or array, specified as a positive scalar integer. Number of antenna ports specified in this property must be equal to the number of antenna ports in EmbeddedE property.

Example: 2

Data Types: double

`FieldFrequency` — Frequencies used to measure electric field
1e9 (default) | scalar | `F`-by-1 vector

Frequencies at which the electric field of the antenna or array was measured, specified as a scalar for a single frequency or a F-by-1 vector for multiple frequencies, where F is the number of frequencies.

Example: 1e9

Example: [1e9 1.25e9 1.5e9]

Data Types: double

`FieldCoordinate` — Coordinate system for field data
`"rectangular"` (default) | `"polar"`

Coordinate system for the measured field data, specified as a string amongst:

rectangular - Cartesian coordinates, where the points are specified as [x y z].
polar - Spherical coordinates, where the points are specified as [azimuth elevation radial].

Example: "polar"

Data Types: string

`Azimuth` — Azimuth angles used to measure electric field
0 (default) | scalar | `A`-by-1 vector

Azimuth angles used to measure electric field, specified as a scalar or A-by-1 vector in degrees, where A is the number of azimuth angles.

Example: [0:5:90]

Data Types: double

`Elevation` — Elevation angles used to measure electric field
90 (default) | scalar | `E`-by-1 vector

Elevation angles used to measure electric field, specified as a scalar or E-by-1 vector in degrees, where E is the number of elevation angles.

Example: [0:5:90]

Data Types: double

`Sparameters` — Scattering parameters of antenna or array
`"[]"` (default) | `sparameters` object

S-parameters for all excitation ports at each frequency, specified as a sparameters object.

Example: sparameters("sample.s2p")

Example: sparameters(dipole,70e6,50)

Example: sparameters(linearArray,140e6)

Data Types: double

`EmbeddedE` — Electric field of individual element in array
`"[]"` (default) | `P`-by-3-by-`N`-by-`F` 4-D array

Cartesian components (P-by-3) of embedded electric field magnitude in V/m when the FieldCoordinate is "rectangular", for each port (N) at each frequency (F) at each observation point in the Direction property, specified as a 4-D array. Number of points is defined by P.

When the FieldCoordinate is "polar", the three columns in P-by-3 matrix represent azimuth angle, elevation angle, and radial magnitude. Set NumPorts value greater than 1 to enable this property.

Example: Let EmbeddedE = emb in a rectangular coordinate system. To access the electric field data for a single port at a single frequency, use emb(:,:,1,1).

Data Types: double
Complex Number Support: Yes

`TerminationImpedance` — Termination impedance for array elements
50 (default) | real scalar

Impedance to terminate other ports except the excitation port while computing the embedded pattern, specified as a real scalar. Set NumPorts value greater than 1 to enable this property.

Example: 75

Data Types: double

`AmplitudeTaper` — Excitation amplitude of array elements in Volts
1 (default) | positive scalar | positive vector of size 1-by-NumPorts positive vector

Excitation amplitude of array elements in Volts, specified as one of these options:

Positive scalar — Use this value to specify uniform amplitude across the individual elements.
Positive vector of size 1-by-NumPorts — Use this value to specify non-uniform amplitude across the individual elements.

The default AmplitudeTaper is 1 Volt.

Example: 2

Example: [2 4]

Data Types: double

`PhaseShift` — Phase shift of array elements in degrees
0 (default) | numeric scalar | numeric vector of size 1-by-NumPorts

Phase shift of array elements in degrees, specified as one of these options:

Numeric scalar — Use this value to specify uniform phase shift across the individual elements.
Numeric vector of size 1-by-NumPorts — Use this value to specify non-uniform phase shift across the individual elements.

The default PhaseShift is zero degrees. PhaseShift values correspond to the respective excitation voltages of the individual elements in the array.

Example: 45

Example: [45 -45]

Data Types: double

`CalculateTotalField` — Option to calculate total electric field from embedded field data
`false` or `0` (default) | `true` or `1`

Option to calculate the total electric field from embedded field data, specified as one of these options:

Numeric or logical 0(false) — Use this value to disable this option.
Numeric or logical 1(true) — Use this value to enable this option.

By default, this option is disabled. When this option is enabled, the EHfields and pattern functions use the calculated total electric field in their results.

Example: true

Data Types: logical

Object Functions

`EHfields`	Electric and magnetic fields of antennas or embedded electric and magnetic fields of antenna element in arrays
`pattern`	Plot radiation pattern of antenna, array, or embedded element of array
`sparameters`	Calculate S-parameters for antenna or array

Note

When measuredAntenna is an input argument to the above functions:

The EHfields function can be used only to visualize the E-field data contained in the E property of the measuredAntenna.
The pattern function can have its Type argument set to only efield.
The sparameters function plots the S-parameters when no output argument is specified or creates a sparameters object when an output argument is specified.

Examples

collapse all

Excite Parabolic Reflector Using E-field Data

Open Live Script

This example shows how to use the measured electric field data of a dipole antenna to excite a parabolic reflector structure. The example uses EHfields function to generate the electric field data. You can import the electric field data of any external antenna into the measuredAntenna object. The electric field magnitude is expressed in V/m and coordinates are expressed in meters and degrees.

Create Dipole antenna, save field data and plot electric field

Design a dipole antenna operating at 10 GHz. Save the complex E-field data of this dipole antenna in a variable.

freq = 10e9;
ant = design(dipole(Tilt=90,TiltAxis=[0 1 0]),freq);
E = EHfields(ant,freq)

E = 3×441 complex

  12.2492 +50.7204i  10.9830 +50.0817i   7.2868 +48.1070i   1.4638 +44.6408i  -5.9963 +39.4936i -14.4447 +32.5478i -23.1139 +23.9147i -31.1701 +14.1574i -37.7710 + 4.5564i -42.1360 - 2.7961i -43.6684 - 5.6012i -42.1360 - 2.7961i -37.7710 + 4.5564i -31.1701 +14.1574i -23.1139 +23.9147i -14.4447 +32.5478i  -5.9963 +39.4936i   1.4638 +44.6408i   7.2868 +48.1070i  10.9830 +50.0817i  12.2492 +50.7204i  12.2492 +50.7204i  11.1051 +50.1436i   7.7649 +48.3712i   2.5080 +45.2950i  -4.2156 +40.7988i -11.8109 +34.8519i -19.5772 +27.6408i -26.7579 +19.7300i -32.6013 +12.2039i -36.4360 + 6.6227i -37.7749 + 4.5369i -36.4360 + 6.6227i -32.6013 +12.2039i -26.7579 +19.7300i -19.5772 +27.6408i -11.8109 +34.8519i  -4.2156 +40.7988i   2.5080 +45.2950i   7.7649 +48.3712i  11.1051 +50.1436i  12.2492 +50.7204i  12.2492 +50.7204i  11.4228 +50.3047i   9.0112 +49.0475i   5.2258 +46.9296i   0.4051 +43.9584i  -5.0085 +40.2214i -10.5012 +35.9467i -15.5309 +31.5501i
   0.0191 + 0.0071i   0.0155 + 0.0116i   0.0115 + 0.0155i   0.0072 + 0.0187i   0.0027 + 0.0210i  -0.0020 + 0.0221i  -0.0065 + 0.0223i  -0.0106 + 0.0218i  -0.0137 + 0.0210i  -0.0158 + 0.0203i  -0.0165 + 0.0201i  -0.0158 + 0.0203i  -0.0137 + 0.0210i  -0.0106 + 0.0218i  -0.0065 + 0.0223i  -0.0020 + 0.0221i   0.0027 + 0.0210i   0.0072 + 0.0187i   0.0115 + 0.0155i   0.0155 + 0.0116i   0.0191 + 0.0071i   0.0191 + 0.0071i  -0.3208 - 0.2160i  -1.3069 - 0.9109i  -2.8600 - 2.1211i  -4.8516 - 3.8972i  -7.1112 - 6.2625i  -9.4357 - 9.1600i -11.6018 -12.3805i -13.3806 -15.4882i -14.5582 -17.8213i -14.9717 -18.6996i -14.5582 -17.8213i -13.3806 -15.4882i -11.6018 -12.3805i  -9.4357 - 9.1600i  -7.1112 - 6.2625i  -4.8516 - 3.8972i  -2.8600 - 2.1211i  -1.3069 - 0.9109i  -0.3208 - 0.2160i   0.0191 + 0.0071i   0.0191 + 0.0071i  -0.5280 - 0.3556i  -2.1176 - 1.4606i  -4.6137 - 3.3253i  -7.7981 - 5.9465i -11.3836 - 9.2543i -15.0340 -13.0573i -18.3899 -16.9940i
   0.0000 + 0.0001i  -7.2267 - 4.8924i -13.8167 - 9.7575i -19.1754 -14.4814i -22.7937 -18.7870i -24.2914 -22.1762i -23.4561 -23.9067i -20.2734 -23.0454i -14.9513 -18.7079i  -7.9486 -10.6411i   0.0000 + 0.0000i   7.9486 +10.6411i  14.9513 +18.7079i  20.2734 +23.0454i  23.4561 +23.9067i  24.2914 +22.1762i  22.7937 +18.7870i  19.1754 +14.4814i  13.8167 + 9.7575i   7.2267 + 4.8924i  -0.0000 - 0.0001i   0.0000 + 0.0001i  -6.8731 - 4.6457i -13.1344 - 9.2239i -18.2136 -13.5889i -21.6250 -17.4521i -23.0095 -20.3392i -22.1726 -21.5919i -19.1151 -20.4533i -14.0568 -16.3107i  -7.4547 - 9.1466i   0.0000 + 0.0000i   7.4547 + 9.1466i  14.0568 +16.3107i  19.1151 +20.4533i  22.1726 +21.5919i  23.0095 +20.3392i  21.6250 +17.4521i  18.2136 +13.5889i  13.1344 + 9.2239i   6.8731 + 4.6457i  -0.0000 - 0.0001i   0.0000 + 0.0001i  -5.8454 - 3.9358i -11.1561 - 7.7223i -15.4375 -11.1610i -18.2748 -13.9710i -19.3715 -15.7815i -18.5823 -16.1686i -15.9384 -14.7525i

Plot the electric field vectors of this dipole antenna.

fig = figure; 
EHfields(ant,freq,ViewField="E");

Figure contains 2 axes objects and another object of type uicontrol. Axes object 1 with title Electric Field, xlabel X, ylabel Y contains an object of type quiver. Axes object 2 contains 3 objects of type patch, surface.

Extract coordinates of electric field points and pass field data to measuredAntenna

Extract the Cartesian coordinates of direction vectors from the electric field plot using quiver. Convert these Cartesian coordinates into spherical coordinates using cart2sph function.

quH = fig.Children(3).Children;
pts = [quH.XData;quH.YData;quH.ZData];
[phi,theta,radius] = cart2sph(pts(1,:),pts(2,:),pts(3,:));
dir = [rad2deg(phi)' 90-rad2deg(theta)' radius'];

Create a measuredAntenna object and pass the electric field data (in V/m.), spherical coordinates of the electric field points, and the phase center of the this field to the respective properties of the measuredAntenna object.

ms = measuredAntenna;
ms.E = E';
ms.Direction = dir;
lambda = 3e8/freq;
f = 5 * lambda;
ms.PhaseCenter = [0 0 f];
ms.FieldFrequency = freq;

Create parabolic reflector antenna with measuredAntenna as exciter

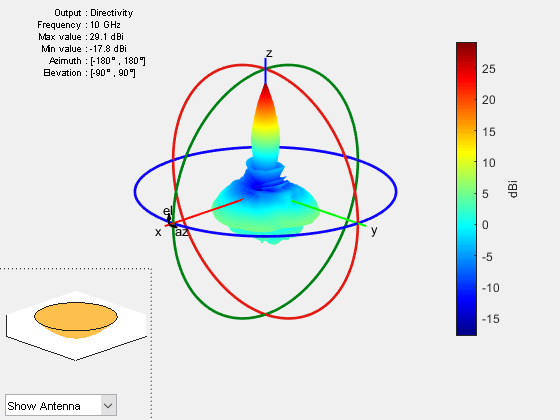
Create a parabolic reflector antenna with the measuredAntenna data as Exciter. Plot the radiation pattern of this antenna at 10 GHz.

back = reflectorParabolic;
back.Exciter = ms;
figure
pattern(back,10e9)

Figure contains 2 axes objects and other objects of type uicontrol. Axes object 1 contains 3 objects of type patch, surface. Hidden axes object 2 contains 17 objects of type surface, line, text, patch.

Import and Visualize Measured Radiation Pattern Data

Open Live Script

This example shows how to import and analyze the measured pattern data of a linear array.

Import Measured Pattern Data

Define the frequency range of the data and number of antenna elements in the array. Import the data from a text file using readmatrix function.

The text file contains measured field data for a linear array of dipoles at 3 frequencies 1.6GHz, 2GHz, and 2.4GHz.

fRange = [1.6e9 2e9 2.4e9];
numAnt = 2;
patternData = readmatrix("MeasuredData.txt");
patternData

patternData = 2701×30 complex
10² ×

   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.8000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.7500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.7000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.6500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.6000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.5500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.5000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.4500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.4000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.3500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.3000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.2500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.2000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.1500 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -1.1000 + 0.0000i  -0.9000 + 0.0000i   0.1500 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i
      ⋮

Extract the field data, direction data, and embedded field data from the imported data. Further, extract azimuth and elevation data from the direction data.

% E-field data
eField(:,:,1) = patternData(:,1:3);
eField(:,:,2) = patternData(:,4:6);
eField(:,:,3) = patternData(:,7:9);

% Direction, azimuth, and elevation data
dir = patternData(:,10:12);
az = dir(1:73,1);
el = dir(1:73:end,2);

% Embedded E-field data
embE(:,:,1,1) = patternData(:,13:15);
embE(:,:,2,1) = patternData(:,16:18);
embE(:,:,1,2) = patternData(:,19:21);
embE(:,:,2,2) = patternData(:,22:24);
embE(:,:,1,3) = patternData(:,25:27);
embE(:,:,2,3) = patternData(:,28:30);

Import and extract S-parameters data from Touchstone files.

% Import S-parameters data
sParamData1 = sparameters("Parameters_1.6ghz.s2p");
sParamData2 = sparameters("Parameters_2ghz.s2p");
sParamData3 = sparameters("Parameters_2.4ghz.s2p");

% Extract S-parameters data
sParam(:,:,1) = sParamData1.Parameters;
sParam(:,:,2) = sParamData2.Parameters;
sParam(:,:,3) = sParamData3.Parameters;
sParamFreq(:,1) = sParamData1.Frequencies;
sParamFreq(:,2) = sParamData2.Frequencies;
sParamFreq(:,3) = sParamData3.Frequencies;
sParam

sParam = 
sParam(:,:,1) =

   0.6991 - 0.5140i   0.0523 + 0.0366i
   0.0523 + 0.0366i   0.6991 - 0.5140i


sParam(:,:,2) =

   0.2076 - 0.0674i  -0.0918 - 0.1830i
  -0.0918 - 0.1830i   0.2076 - 0.0674i


sParam(:,:,3) =

   0.6581 + 0.2567i  -0.0490 + 0.0871i
  -0.0490 + 0.0871i   0.6581 + 0.2567i

sParamFreq

sParamFreq = 1×3
10⁹ ×

    1.6000    2.0000    2.4000

s = sparameters(sParam,sParamFreq);

Assign Data to measuredAntenna

Assign the extracted data to a measuredAntenna object.

mesAnt = measuredAntenna(E=eField, Direction=dir, NumPorts=numAnt,...
                Azimuth=az, Elevation=el, FieldCoordinate="polar",...
                EmbeddedE=embE, FieldFrequency=fRange, Sparameters=s)

mesAnt = 
  measuredAntenna with properties:

                       E: [2701×3×3 double]
               Direction: [2701×3 double]
             PhaseCenter: [0 0 0.0750]
                NumPorts: 2
          FieldFrequency: [3×1 double]
         FieldCoordinate: "polar"
                 Azimuth: [-180 -175 -170 -165 -160 -155 -150 -145 -140 -135 -130 -125 -120 -115 -110 -105 -100 -95 -90 -85 -80 -75 -70 -65 -60 -55 -50 -45 -40 -35 -30 -25 -20 -15 -10 -5 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 … ] (1×73 double)
               Elevation: [-90 -85 -80 -75 -70 -65 -60 -55 -50 -45 -40 -35 -30 -25 -20 -15 -10 -5 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90]
             Sparameters: [1×1 sparameters]
          AmplitudeTaper: 1
              PhaseShift: 0
               EmbeddedE: [2701×3×2×3 double]
    TerminationImpedance: 50
     CalculateTotalField: 0

Visualize Measured Pattern Data

Plot the radiation pattern and electric field for this measuredAntenna at 2GHz, while plot S-parameters over the entire frequency range.

pattern(mesAnt,fRange(2),Type="efield")

Figure contains an axes object and other objects of type uicontrol. The hidden axes object contains 16 objects of type line, text, patch, surface.

EHfields(mesAnt,fRange(2))

Figure contains an axes object. The axes object with title Electric Field, xlabel X, ylabel Y contains an object of type quiver. This object represents E.

sp = sparameters(mesAnt,fRange);
rfplot(sp)

$Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Magnitude (dB) contains 4 objects of type line. These objects represent dB(S_{11}), dB(S_{21}), dB(S_{12}), dB(S_{22}).$

Import and Visualize Radiation Pattern Data from FFD File

Open Live Script

This example shows how to import radiation pattern data from a .ffd file to workspace and visualize it. The .ffd file contains far-field data generated by the HFSS™ software. The data is visualized using object functions of the measuredAntenna object.

Load the radiation pattern data from the .ffd file into the workspace by using the loadData helper function (defined in the supporting function section of this example). Specify the coordinate system angle convention used for this data in the .ffd file.

fileName = sprintf("RefFFDdata.ffd");
CoordinateSystem = "Phi-Theta";
[theta1,phi1,numFreqs,Etheta,Ephi,freqs] = loadData(fileName,CoordinateSystem);
if CoordinateSystem == "Phi-Theta"
    elev = 90 - theta1;
else
    elev = theta1;
end

Calculate the number of data points.

numPt = numel(theta1)*numel(phi1);

Extract the electric field data from the data in the workspace.

ESph = [Ephi;Etheta;zeros(numPt,3)];
eField = reshape(ESph,numPt,3,numFreqs);

Calculate the spherical coordinates of the electric field points.

lambda = 3e8/max(freqs);
radius = 100*lambda*ones(numPt,1);
[theta,phi] = meshgrid(elev,phi1);
phi = phi(:);
theta = theta(:);
direction = [phi theta radius];

Create a measuredAntenna object with number of ports equal to those present in the .ffd file data. Set the E property value to eField. Set the Direction property using calculated spherical coordinates. Set the Azimuth property to phi1 and Elevation property to elev. Specify the phase center. This example assumes the phase center at (0,0,0). Set the FieldFrequency property using the frequencies of the electric field data.

mAnt = measuredAntenna(NumPorts=1);
mAnt.E = eField;
mAnt.Direction = direction;
mAnt.PhaseCenter = [0 0 0];
mAnt.FieldFrequency = freqs;
mAnt.Azimuth = phi1;
mAnt.Elevation = elev;
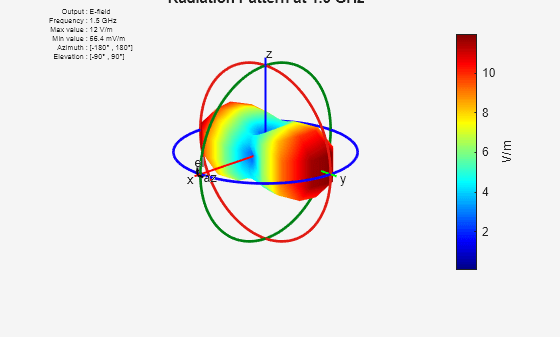
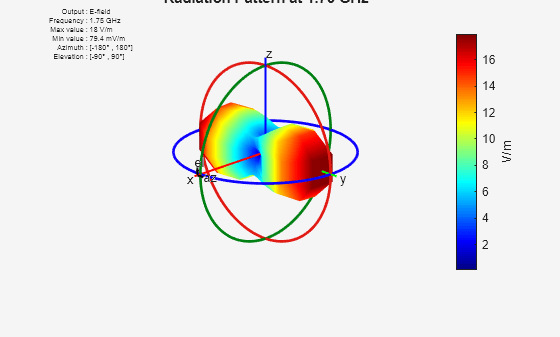
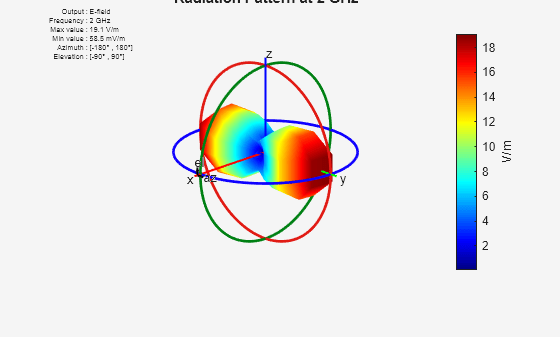
mAnt.FieldCoordinate = 'polar';

Visualize the radiation patterns at the individual frequencies.

for i=1:numFreqs
figure
pattern(mAnt,freqs(i))
title(strcat("Radiation Pattern at ",num2str(freqs(i)/1e9)," GHz"))
end

Figure contains an axes object and other objects of type uicontrol. The hidden axes object with title Radiation Pattern at 1.5 GHz contains 16 objects of type line, text, patch, surface.

Figure contains an axes object and other objects of type uicontrol. The hidden axes object with title Radiation Pattern at 1.75 GHz contains 16 objects of type line, text, patch, surface.

Figure contains an axes object and other objects of type uicontrol. The hidden axes object with title Radiation Pattern at 2 GHz contains 16 objects of type line, text, patch, surface.

Visualize the corresponding electric fields.

for i=1:numFreqs
figure
EHfields(mAnt,freqs(i))
title(strcat("Electric Field at ",num2str(freqs(i)/1e9)," GHz"))
end

Figure contains an axes object. The axes object with title Electric Field at 1.5 GHz, xlabel X, ylabel Y contains an object of type quiver. This object represents E.

Figure contains an axes object. The axes object with title Electric Field at 1.75 GHz, xlabel X, ylabel Y contains an object of type quiver. This object represents E.

Figure contains an axes object. The axes object with title Electric Field at 2 GHz, xlabel X, ylabel Y contains an object of type quiver. This object represents E.

Supporting Function

The loadData helper function extracts the number of frequencies, angle values for the data points, and the electric field values from the .ffd file.

function [theta1,phi1,numFreqs,Etheta,Ephi,freqs] = loadData(fileName,CoordinateSystem)
fid = fopen(fileName);

if CoordinateSystem == "Phi-Theta"
    numHeaderLines = 3;
else
    textscan(fid,'%s',1);
    numHeaderLines = 4;
end

data = num2cell(fscanf(fid,'%d',3));
theta1 = linspace(data{:});
data = num2cell(fscanf(fid,'%d',3));
phi1 = linspace(data{:});
C1 = textscan(fid,'%s %d',1);
numFreqs = C1{2};
fclose(fid);

Mfull = readmatrix(fileName,FileType="text",NumHeaderLines=numHeaderLines);
freqs = Mfull(isnan(Mfull(:,1)),2);
MData = Mfull(~isnan(Mfull(:,1)),:);
Etheta = reshape(MData(:,1) + 1j*MData(:,2),length(phi1)*length(theta1),[]);
Ephi = reshape(MData(:,3) + 1j*MData(:,4),length(phi1)*length(theta1),[]);
end

Use Measured Antenna Object in Antenna Block

This example uses:

Open Script

This example shows how to use measuredAntenna object in the Antenna block to model a measured antenna or array characterized by means of its S-parameters and frequency dependent far-field radiation pattern including both polarization components. The measuredAntenna object lets you replace the physical antennas from the antenna catalog with measured field data of the antenna. This example extracts data from a linear array to create a measuredAntenna object using hcreate_mAnt helper function.

System Configuration

Define the carrier frequency in Hz and set it in these parameters:

Radiated carrier frequency parameter in the Transmit Antenna block
Incident carrier frequency parameter in the Receiver Antenna block
Carrier frequencies parameter in the Inport and Outport blocks

FreqCarrier = 5e9;

Define gain for the Gain block. This Gain block acts as a free-space path-loss channel.

lambdaCarrier = physconst('lightspeed')/FreqCarrier; %[m]

Define the input impedance of the low noise amplifier (LNA) in ohms.

Zin_r =71.3819 - 1j*2.1795;

Define the available input power in dBm for the two RF transmitter chains and assign the variables to Pin 1 and Pin 2 in the Constant block.

Pin1 = -30;
Pin2 = -30;

Create a linear antenna array and extract data from it to create a measuredAntenna object. The data extracted from the linear array is a substitute of real-world measured data that can be inputted by changing the hcreate_mAnt helper function so as to read the embedded electric fields from data file.

dist = lambdaCarrier*0.5;
d1 = design(dipole,FreqCarrier);
antElems = [d1 copy(d1)];
la = linearArray('Element',antElems,'ElementSpacing',dist);
la.TiltAxis = [0 1 0];
la.Tilt = 90;
freqRange = (4.5:0.05:5.5)*1e9;
[mAnt,R] = hcreate_mAnt(la,freqRange);

Compute impedances in ohms for PA and PA1 Amplifier blocks in the transmitter.

z = impedance(la,freqRange);
z = z(freqRange==FreqCarrier,:);
Zin_t1 = z(1);
Zin_t2 = z(2);

Simulate Model

Open and simulate the measuredAnt.slx model. Observe the output power at the receiver.

open_system("measuredAnt.slx")
sim("measuredAnt.slx");

Version History

Introduced in R2023a

expand all

R2024a: Calculate total electric field using embedded field data

Calculate the total electric field of an array from the embedded field, excitation amplitude, and phase shift of the individual antenna elements in the array. Use this calculated total electric field in the field analysis of the array using the pattern and EHfields functions.

R2023b: Perform field and port analysis on measured field data

Perform field and port analysis using pattern, EHfields, and sparameters on:

The electric field and S-parameters data of an antenna
The total electric field, embedded electric field, and S-parameters data of an array

measured at multiple frequencies.

measuredAntenna

Description

Creation

Syntax

Description

Properties

`E` — Magnitude of radiated electric field
`[0.1 0.1 0.1]` (default) | `P`-by-3-by-`F` matrix

`Direction` — Direction of radiated electric field
`[0 90 100]` (default) | `P`-by-3 matrix

`PhaseCenter` — Phase center of measured antenna
`[0 0 0.075]` (default) | 1-by-3 vector

`NumPorts` — Number of excitation ports
1 (default) | positive scalar integer

`FieldFrequency` — Frequencies used to measure electric field
1e9 (default) | scalar | `F`-by-1 vector

`FieldCoordinate` — Coordinate system for field data
`"rectangular"` (default) | `"polar"`

`Azimuth` — Azimuth angles used to measure electric field
0 (default) | scalar | `A`-by-1 vector

`Elevation` — Elevation angles used to measure electric field
90 (default) | scalar | `E`-by-1 vector

`Sparameters` — Scattering parameters of antenna or array
`"[]"` (default) | `sparameters` object

`EmbeddedE` — Electric field of individual element in array
`"[]"` (default) | `P`-by-3-by-`N`-by-`F` 4-D array

`TerminationImpedance` — Termination impedance for array elements
50 (default) | real scalar

`AmplitudeTaper` — Excitation amplitude of array elements in Volts
1 (default) | positive scalar | positive vector of size 1-by-NumPorts positive vector

`PhaseShift` — Phase shift of array elements in degrees
0 (default) | numeric scalar | numeric vector of size 1-by-NumPorts

`CalculateTotalField` — Option to calculate total electric field from embedded field data
`false` or `0` (default) | `true` or `1`

Object Functions

Examples

Excite Parabolic Reflector Using E-field Data

Import and Visualize Measured Radiation Pattern Data

Import and Visualize Radiation Pattern Data from FFD File

Use Measured Antenna Object in Antenna Block

Version History

R2024a: Calculate total electric field using embedded field data

R2023b: Perform field and port analysis on measured field data

See Also

Objects

measuredAntenna

Description

Creation

Syntax

Description

Properties

E — Magnitude of radiated electric field [0.1 0.1 0.1] (default) | P-by-3-by-F matrix

Direction — Direction of radiated electric field [0 90 100] (default) | P-by-3 matrix

PhaseCenter — Phase center of measured antenna [0 0 0.075] (default) | 1-by-3 vector

NumPorts — Number of excitation ports 1 (default) | positive scalar integer

FieldFrequency — Frequencies used to measure electric field 1e9 (default) | scalar | F-by-1 vector

FieldCoordinate — Coordinate system for field data "rectangular" (default) | "polar"

Azimuth — Azimuth angles used to measure electric field 0 (default) | scalar | A-by-1 vector

Elevation — Elevation angles used to measure electric field 90 (default) | scalar | E-by-1 vector

Sparameters — Scattering parameters of antenna or array "[]" (default) | sparameters object

EmbeddedE — Electric field of individual element in array "[]" (default) | P-by-3-by-N-by-F 4-D array

TerminationImpedance — Termination impedance for array elements 50 (default) | real scalar

AmplitudeTaper — Excitation amplitude of array elements in Volts 1 (default) | positive scalar | positive vector of size 1-by-NumPorts positive vector

PhaseShift — Phase shift of array elements in degrees 0 (default) | numeric scalar | numeric vector of size 1-by-NumPorts

CalculateTotalField — Option to calculate total electric field from embedded field data false or 0 (default) | true or 1

Object Functions

Examples

Excite Parabolic Reflector Using E-field Data

Import and Visualize Measured Radiation Pattern Data

Import and Visualize Radiation Pattern Data from FFD File

Use Measured Antenna Object in Antenna Block

Version History

R2024a: Calculate total electric field using embedded field data

R2023b: Perform field and port analysis on measured field data

See Also

Objects

`E` — Magnitude of radiated electric field
`[0.1 0.1 0.1]` (default) | `P`-by-3-by-`F` matrix

`Direction` — Direction of radiated electric field
`[0 90 100]` (default) | `P`-by-3 matrix

`PhaseCenter` — Phase center of measured antenna
`[0 0 0.075]` (default) | 1-by-3 vector

`NumPorts` — Number of excitation ports
1 (default) | positive scalar integer

`FieldFrequency` — Frequencies used to measure electric field
1e9 (default) | scalar | `F`-by-1 vector

`FieldCoordinate` — Coordinate system for field data
`"rectangular"` (default) | `"polar"`

`Azimuth` — Azimuth angles used to measure electric field
0 (default) | scalar | `A`-by-1 vector

`Elevation` — Elevation angles used to measure electric field
90 (default) | scalar | `E`-by-1 vector

`Sparameters` — Scattering parameters of antenna or array
`"[]"` (default) | `sparameters` object

`EmbeddedE` — Electric field of individual element in array
`"[]"` (default) | `P`-by-3-by-`N`-by-`F` 4-D array

`TerminationImpedance` — Termination impedance for array elements
50 (default) | real scalar

`AmplitudeTaper` — Excitation amplitude of array elements in Volts
1 (default) | positive scalar | positive vector of size 1-by-NumPorts positive vector

`PhaseShift` — Phase shift of array elements in degrees
0 (default) | numeric scalar | numeric vector of size 1-by-NumPorts

`CalculateTotalField` — Option to calculate total electric field from embedded field data
`false` or `0` (default) | `true` or `1`