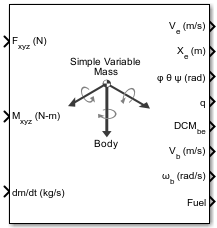
Simple Variable Mass 6DOF (Quaternion)
Implement quaternion representation of six-degrees-of-freedom equations of motion of simple variable mass with respect to body axes
Libraries:
Aerospace Blockset /
Equations of Motion /
6DOF
Alternative Configurations of Simple Variable Mass 6DOF (Quaternion) Block:
6DOF (Quaternion) | Custom Variable Mass 6DOF (Quaternion)
Description
The Simple Variable Mass 6DOF (Quaternion) implements a quaternion representation of six-degrees-of-freedom equations of motion of simple variable mass with respect to body axes.
For a description of the coordinate system and the translational dynamics, see the description for the Simple Variable Mass 6DOF (Euler Angles) block. Aerospace Blockset™ uses quaternions that are defined using the scalar-first convention. For more information on the integration of the rate of change of the quaternion vector, see Algorithms.
The Simple Variable Mass 6DOF (Quaternion), 6DOF (Quaternion), and Custom Variable Mass 6DOF (Quaternion) blocks are alternative configurations of the same block.
Simple Variable Mass 6DOF (Quaternion) — Implement quaternion representation of six-degrees-of-freedom equations of motion of simple variable mass with respect to body axes
6DOF (Quaternion) — Implement quaternion representation of six-degrees-of-freedom equations of motion with respect to body axes
Custom Variable Mass 6DOF (Quaternion) — Implement quaternion representation of six-degrees-of-freedom equations of motion of custom variable mass with respect to body axes
Limitations
The block assumes that the applied forces are acting at the center of gravity of the body.
Ports
Input
Output
Parameters
Alternative Configurations
Algorithms
The equation of the integration of the rate of change of the quaternion vector follows. The gain K drives the norm of the quaternion state vector to 1.0 should ε become nonzero. You must choose the value of this gain with care, because a large value improves the decay rate of the error in the norm, but also slows the simulation because fast dynamics are introduced. An error in the magnitude in one element of the quaternion vector is spread equally among all the elements, potentially increasing the error in the state vector.
References
[1] Stevens, Brian, and Frank Lewis. Aircraft Control and Simulation. 2nd ed. Hoboken, NJ: John Wiley & Sons, 2003.
[2] Zipfel, Peter H. Modeling and Simulation of Aerospace Vehicle Dynamics. 2nd ed. Reston, VA: AIAA Education Series, 2007.
Extended Capabilities
Version History
Introduced in R2006aSee Also
6DOF (Euler Angles) | 6DOF (Quaternion) | 6DOF ECEF (Quaternion) | 6DOF Wind (Quaternion) | 6DOF Wind (Wind Angles) | Custom Variable Mass 6DOF (Euler Angles) | Custom Variable Mass 6DOF (Quaternion) | Custom Variable Mass 6DOF ECEF (Quaternion) | Custom Variable Mass 6DOF Wind (Quaternion) | Custom Variable Mass 6DOF Wind (Wind Angles) | Simple Variable Mass 6DOF (Euler Angles) | Simple Variable Mass 6DOF ECEF (Quaternion) | Simple Variable Mass 6DOF Wind (Quaternion) | Simple Variable Mass 6DOF Wind (Wind Angles)