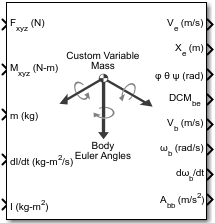
Custom Variable Mass 6DOF (Euler Angles)

Implement Euler angle representation of six-degrees-of-freedom equations of motion of custom variable mass

• 

×

Libraries:
Aerospace Blockset / Equations of Motion / 6DOF

Description

The Custom Variable Mass 6DOF (Euler Angles) block implements the Euler angle representation of six-degrees-of-freedom equations of motion of custom variable mass. It considers the rotation of a body-fixed coordinate frame (X_b, Y_b, Z_b) about a flat Earth reference frame (X_e, Y_e, Z_e). For more information on Euler angles, see Algorithms.

Limitations

The block assumes that the applied forces act at the center of gravity of the body.

Ports

Input

F_xyz — Applied forces

three-element vector

Applied forces, specified as a three-element vector.

Data Types: double

M_xyz — Applied moments

three-element vector

Applied moments, specified as a three-element vector.

Data Types: double

dm/dt — Rates of change of mass

three-element vector

One or more rates of change of mass (positive if accreted, negative if ablated), specified as a three-element vector.

Dependencies

To enable this port, select Include mass flow relative velocity.

Data Types: double

m — Mass

scalar

Mass, specified as a scalar.

Data Types: double

dI/dt — Rate of change of inertia tensor matrix

3-by-3 matrix

Rate of change of inertia tensor matrix, specified as a 3-by-3 matrix.

Data Types: double

I — Inertia tensor matrix

3-by-3 matrix

Inertia tensor matrix, specified as a 3-by-3 matrix.

Data Types: double

V_re — Relative velocities

three-element vector

One or more relative velocities at which the mass is accreted to or ablated from the body in body-fixed axes, specified as a three-element vector.

Dependencies

To enable this port, select Include mass flow relative velocity.

Data Types: double

Output

V_e — Velocity in flat Earth reference frame

three-element vector

Velocity in the flat Earth reference frame, returned as a three-element vector.

Data Types: double

X_e — Position in flat Earth reference frame

three-element vector

Position in the flat Earth reference frame, returned as a three-element vector.

Data Types: double

φ θ ψ (rad) — Euler rotation angles

three-element vector

Euler rotation angles [roll, pitch, yaw], returned as a three-element vector, in radians.

Data Types: double

DCM_be — Coordinate transformation

3-by-3 matrix

Coordinate transformation from flat Earth axes to body-fixed axes, returned as a 3-by-3 matrix.

Data Types: double

V_b — Velocity in body-fixed frame

three-element vector

Velocity in body-fixed frame, returned as a three-element vector.

Data Types: double

ω_b (rad/s) — Angular rates in body-fixed axes

three-element vector

Angular rates in body-fixed axes, returned as a three-element vector, in radians per second.

Data Types: double

dω_b/dt — Angular accelerations

three-element vector

Angular accelerations in body-fixed axes, returned as a three-element vector, in radians per second squared.

Data Types: double

A_bb — Accelerations in body-fixed axes

three-element vector

Accelerations in body-fixed axes with respect to body frame, returned as a three-element vector.

Data Types: double

A_be — Accelerations with respect to inertial frame

three-element vector

Accelerations in body-fixed axes with respect to inertial frame (flat Earth), returned as a three-element vector. You typically connect this signal to the accelerometer.

Dependencies

This port appears only when the Include inertial acceleration check box is selected.

Data Types: double

Parameters

Main

Units — Input and output units

Metric (MKS) (default) | English (Velocity in ft/s) | English (Velocity in kts)

Input and output units, specified as Metric (MKS), English (Velocity in ft/s), or English (Velocity in kts).

Units	Forces	Moment	Acceleration	Velocity	Position	Mass	Inertia
Metric (MKS)	Newton	Newton-meter	Meters per second squared	Meters per second	Meters	Kilogram	Kilogram meter squared
English (Velocity in ft/s)	Pound	Foot-pound	Feet per second squared	Feet per second	Feet	Slug	Slug foot squared
English (Velocity in kts)	Pound	Foot-pound	Feet per second squared	Knots	Feet	Slug	Slug foot squared

Programmatic Use

Block Parameter: units

Type: character vector

Values: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts)

Default: Metric (MKS)

Mass type — Mass type

Custom Variable (default) | Simple Variable | Fixed

Mass type, specified according to the following table.

Mass Type	Description	Default for
Fixed	Mass is constant throughout the simulation.	6DOF (Euler Angles) 6DOF (Quaternion) 6DOF Wind (Wind Angles) 6DOF Wind (Quaternion) 6DOF ECEF (Quaternion)
Simple Variable	Mass and inertia vary linearly as a function of mass rate.	Simple Variable Mass 6DOF (Euler Angles) Simple Variable Mass 6DOF (Quaternion) Simple Variable Mass 6DOF Wind (Wind Angles) Simple Variable Mass 6DOF Wind (Quaternion) Simple Variable Mass 6DOF ECEF (Quaternion)
Custom Variable	Mass and inertia variations are customizable.	Custom Variable Mass 6DOF (Euler Angles) Custom Variable Mass 6DOF (Quaternion) Custom Variable Mass 6DOF Wind (Wind Angles) Custom Variable Mass 6DOF Wind (Quaternion) Custom Variable Mass 6DOF ECEF (Quaternion)

The Custom Variable selection conforms to the previously described equations of motion.

Programmatic Use

Block Parameter: mtype

Type: character vector

Values: Fixed | Simple Variable | Custom Variable

Default: 'Custom Variable'

Representation — Equations of motion representation

Euler Angles (default) | Quaternion

Equations of motion representation, specified according to the following table.

Representation	Description
Euler Angles	Use Euler angles within equations of motion.
Quaternion	Use quaternions within equations of motion.

The Quaternion selection conforms to the equations of motion in Algorithms.

Programmatic Use

Block Parameter: rep

Type: character vector

Values: Euler Angles | Quaternion

Default: 'Euler Angles'

Initial position in inertial axes [Xe,Ye,Ze] — Position in inertial axes

[0 0 0] (default) | three-element vector

Initial location of the body in the flat Earth reference frame, specified as a three-element vector.

Programmatic Use

Block Parameter: xme_0

Type: character vector

Values: '[0 0 0]' | three-element vector

Default: '[0 0 0]'

Initial velocity in body axes [U,v,w] — Velocity in body axes

[0 0 0] (default) | three-element vector

Initial velocity in body axes, specified as a three-element vector, in the body-fixed coordinate frame.

Programmatic Use

Block Parameter: Vm_0

Type: character vector

Values: '[0 0 0]' | three-element vector

Default: '[0 0 0]'

Initial Euler orientation [roll, pitch, yaw] — Initial Euler orientation

[0 0 0] (default) | three-element vector

Initial Euler orientation angles [roll, pitch, yaw], specified as a three-element vector, in radians. Euler rotation angles are those between the body and north-east-down (NED) coordinate systems.

Programmatic Use

Block Parameter: eul_0

Type: character vector

Values: '[0 0 0]' | three-element vector

Default: '[0 0 0]'

Initial body rotation rates [p,q,r] — Initial body rotation

[0 0 0] (default) | three-element vector

Initial body-fixed angular rates with respect to the NED frame, specified as a three-element vector, in radians per second.

Programmatic Use

Block Parameter: pm_0

Type: character vector

Values: '[0 0 0]' | three-element vector

Default: '[0 0 0]'

Include mass flow relative velocity — Mass flow relative velocity port

off (default) | on

Select this check box to add a mass flow relative velocity port. This is the relative velocity at which the mass is accreted or ablated.

Programmatic Use

Block Parameter: vre_flag

Type: character vector

Values: off | on

Default: off

Include inertial acceleration — Include inertial acceleration port

off (default) | on

Select this check box to add an inertial acceleration port.

Dependencies

To enable the A_{b ff} port, select this parameter.

Programmatic Use

Block Parameter: abi_flag

Type: character vector

Values: 'off' | 'on'

Default: off

State Attributes

Assign a unique name to each state. You can use state names instead of block paths during linearization.

• To assign a name to a single state, enter a unique name between quotes, for example, 'velocity'.

• To assign names to multiple states, enter a comma-separated list surrounded by braces, for example, {'a', 'b', 'c'}. Each name must be unique.

• If a parameter is empty (' '), no name is assigned.

• The state names apply only to the selected block with the name parameter.

• The number of states must divide evenly among the number of state names.

• You can specify fewer names than states, but you cannot specify more names than states.

  For example, you can specify two names in a system with four states. The first name applies to the first two states and the second name to the last two states.

• To assign state names with a variable in the MATLAB^® workspace, enter the variable without quotes. A variable can be a character vector, cell array, or structure.

Position: e.g., {'Xe', 'Ye', 'Ze'} — Position state name

'' (default) | comma-separated list surrounded by braces

Position state names, specified as a comma-separated list surrounded by braces.

Programmatic Use

Block Parameter: xme_statename

Type: character vector

Values: '' | comma-separated list surrounded by braces

Default: ''

Velocity: e.g., {'U', 'v', 'w'} — Velocity state name

'' (default) | comma-separated list surrounded by braces

Velocity state names, specified as comma-separated list surrounded by braces.

Programmatic Use

Block Parameter: Vm_statename

Type: character vector

Values: '' | comma-separated list surrounded by braces

Default: ''

Euler rotation angles: e.g., {'phi', 'theta', 'psi'} — Euler rotation state name

'' (default) | comma-separated list surrounded by braces

Euler rotation angle state names, specified as a comma-separated list surrounded by braces.

Programmatic Use

Block Parameter: eul_statename

Type: character vector

Values: '' | comma-separated list surrounded by braces

Default: ''

Body rotation rates: e.g., {'p', 'q', 'r'} — Body rotation state names

'' (default) | comma-separated list surrounded by braces

Body rotation rate state names, specified comma-separated list surrounded by braces.

Programmatic Use

Block Parameter: pm_statename

Type: character vector

Values: '' | comma-separated list surrounded by braces

Default: ''

Algorithms

The origin of the body-fixed coordinate frame is the center of gravity of the body. The body is assumed to be rigid, which eliminates the need to consider the forces acting between individual elements of mass. The flat Earth reference frame is considered inertial, an excellent approximation that allows the forces due to the Earth's motion relative to the “fixed stars” to be neglected.

The translational motion of the body-fixed coordinate frame is given below, where the applied forces [F_x F_y F_z]^T are in the body-fixed frame. Vre_b is the relative velocity in the body axes at which the mass flow ($$\dot{m}$$) is ejected or added to the body-fixed axes.

$$\begin{array}{l}{\overline{F}}_b=\left[\begin{array}{c}{F}_x\\ F_y\\ F_z\end{array}\right]=m({\dot{\overline{V}}}_b+\overline{\omega }\times {\overline{V}}_b)-\dot{m}\overline{V}r{e}_b\\ A_{be}=\frac{{\overline{F}}_b+\dot{m}{\overline{V}}_{r{e}_b}}{m}\\ A_{bb}=\left[\begin{array}{c}{\dot{u}}_b\\ {\dot{v}}_b\\ {\dot{w}}_b\end{array}\right]=\frac{{\overline{F}}_b+\dot{m}{\overline{V}}_{r{e}_b}}{m}-\overline{\omega }\times {\overline{V}}_b\\ {\overline{V}}_b=\left[\begin{array}{c}{u}_b\\ v_b\\ w_b\end{array}\right],\overline{\omega }=\left[\begin{array}{c}p\\ q\\ r\end{array}\right]\end{array}$$

The rotational dynamics of the body-fixed frame are given below, where the applied moments are [L M N]^T, and the inertia tensor I is with respect to the origin O.

$$\begin{array}{l}{\overline{M}}_B=\left[\begin{array}{c}L\\ M\\ N\end{array}\right]=I\dot{\overline{\omega }}+\overline{\omega }\times (I\overline{\omega })+\dot{I}\overline{\omega }\\ \\ I=\left[\begin{array}{ccc}{I}_{xx}& -I_{xy}& -I_{xz}\\ -I_{yx}& I_{yy}& -I_{yz}\\ -I_{zx}& -I_{zy}& I_{zz}\end{array}\right]\\ \\ \dot{I}=\left[\begin{array}{ccc}{\dot{I}}_{xx}& -{\dot{I}}_{xy}& -{\dot{I}}_{xz}\\ -{\dot{I}}_{yx}& {\dot{I}}_{yy}& -{\dot{I}}_{yz}\\ -{\dot{I}}_{zx}& -{\dot{I}}_{zy}& {\dot{I}}_{zz}\end{array}\right]\end{array}$$

The relationship between the body-fixed angular velocity vector, [p q r]^T, and the rate of change of the Euler angles, $${[\dot{\varphi }\dot{\theta }\dot{\psi }]}^{\text{T}}$$, can be determined by resolving the Euler rates into the body-fixed coordinate frame.

$$\left[\begin{array}{c}p\\ q\\ r\end{array}\right]=\left[\begin{array}{c}\dot{\varphi }\\ 0\\ 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \varphi & \sin \varphi \\ 0& -\sin \varphi & \cos \varphi \end{array}\right]\left[\begin{array}{c}0\\ \dot{\theta }\\ 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \varphi & \sin \varphi \\ 0& -\sin \varphi & \cos \varphi \end{array}\right]\left[\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right]\left[\begin{array}{c}0\\ 0\\ \dot{\psi }\end{array}\right]=J^{-1}\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]$$

Inverting J then gives the required relationship to determine the Euler rate vector.

$$\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]=J\left[\begin{array}{c}p\\ q\\ r\end{array}\right]=\left[\begin{array}{ccc}1& (\sin \varphi \tan \theta )& (\cos \varphi \tan \theta )\\ 0& \cos \varphi & -\sin \varphi \\ 0& \frac{\sin \varphi }{\cos \theta }& \frac{\cos \varphi }{\cos \theta }\end{array}\right]\left[\begin{array}{c}p\\ q\\ r\end{array}\right]$$

For more information on aerospace coordinate systems, see About Aerospace Coordinate Systems.

References

[1] Stevens, Brian, and Frank Lewis. Aircraft Control and Simulation, 2nd ed. Hoboken, NJ: John Wiley & Sons, 2003.

[2] Zipfel, Peter H. Modeling and Simulation of Aerospace Vehicle Dynamics. 2nd ed. Reston, VA: AIAA Education Series, 2007.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2006a