RF Transceiver Design and Antenna Integration
Overview
Throughput requirements for emerging communication systems, radar, and smart location services require high performance and low-cost RF transceivers. For these new broadband systems, transceivers are fully integrated from the baseband digital circuitry through to the antenna array elements.
To properly design these integrated transceivers, accurate RF models are required in the study and development of innovative architectures. Models must operate across multiple bandwidths and account for impedance mismatches, noise, and non-linearity effects.
In this presentation, you will see how MATLAB and Simulink can be used to model integrated RF and antenna arrays where a combination of measured component performance along with data sheet specifications are combined with the full-wave electromagnetic analysis results describing the behavior of the antenna array.
Highlights
- RF system design
- Wide-band antenna design and optimization
- Integration of antenna front-ends and RF transceivers
Recorded: 23 Oct 2020
Welcome to this MathWorks webinar on RF transceiver design and antenna integration. My name is Giorgia Zucchelli. I am the technical marketing manager for MathWorks RF and mixed-signal product areas. If you have any question concerning this presentation or related topics, please feel free to contact me directly via email.
In the next half hour, using code examples and executable models, we will describe how to design RF transceivers, starting from high-level specifications. We will progressively elaborate the design to account for the effects of noise, non-linearity, impedance mismatches, interfering signals, and also include the integration of an antenna.
Understanding the simultaneous impact of each of these effects is challenging to anticipate and to understand. When elaborating the RF system design, we will see how an accurate model of the RF transceiver can help assessing the implementation trade-offs and determine the best architectural implementation. For example, we will see, actually, how to determine such things as the number of up-conversion and down-conversion stages are required, or maybe choosing a particular digital signal processing algorithm required to mitigate impairments.
And the webinar will also help you with answering many more questions that you might have, and also to gain insights in some of your design.
And we start this presentation with an introduction to RF system design. We will use two simple examples. The first example is a monostatic pulse radar. And the second example is a Zigbee wireless communication system. We will demonstrate methodology to design the RF transceivers and achieve a certain set of specification, for example, a maximum bit error rate or certain probability of detection. And more complex RF systems, for example, for 5G application, could be designed following exactly the same methodology.
We will start with RF budget analysis. Then we will elaborate our design to include non-linear effects. Also, we will include interfering signals. And then last, we will integrate electromagnetic simulation results and a full antenna element in our transceiver.
The first example is a very simple radar system. It is composed of a transmitter, a receiver, a channel, and a target model, for which we can specify location and speed. Let's open the model.
This radar is a monostatic pulse radar. It operates at 10GHz with a signal bandwidth of approximately 30 MHz. The model includes the pulse generation, the target reflection, the signal acquisition, and the digital signal processing algorithms. The waveform parameters have been determined using the radar equation. In this model script, you see that the different parameters are set to achieve a max range of 5 kilometers and a resolution of 50 meters.
When we run the simulation, we see that we have a target, this approximately 2 km away from the radar. And the target is detected. Let's see what happens if we move the target farther away from the radar. For instance, let's place it near the limit of the radar detection range at 4.9 km. The target can still be detected, though the peak is just above the noise floor.
If we decrease the RF receiver gain, even just by a couple of dB, the target is not detected anymore and the signal level is below the noise floor. Alternatively, if we increase the noise figure of the receiver, we also see that the reflected target signal falls below the noise floor.
We can conclude that to meet the target range detection requirements, the performance budget for the RF receiver is 30 dB of gain and 10 dB of noise figure. At this point, we can begin to assess implementation trade-offs and answer questions, such as how do we partition the gain and noise budget across the different components of the RF receiver? What about the impact of other effects, such as phase noise, non-linear behavior, or integration of an antenna?
Let's look at another example, a wireless communication system. In this example, there is both a baseband transmitter and a baseband receiver, which can be used to calculate the bit error rate and the chip error rate. To compute a bit error rate, you need to simulate very long sequences of bits, in order to achieve statistically significant results.
In this case, we want to achieve a bit error rate smaller than 1e-4. Calculation of the equivalent chip error rate would require shorter data sequences, as the relative number of errors is higher, given the many bits map into a chip.
For this scenario, a chip error rate of approximately 7% is required to a bit error rate of 1e-4. We will use the chip error rate as a proxy for the bit error rate, so that we can run shorter simulations.
We can derive the specs of the receiver based on the desired the chip error rate. For example, to achieve a 7% chip error rate at the power sensitivity level of -100 dBm, the signal-to-noise ratio of the receiver must be at least 0.3 dB. Higher SNR will allow us to achieve, obviously, a better chip error rate.
Based on the SNR, we can derive the RF receiver budget using heuristics and well known link budget analysis techniques. In this case, for a power sensitivity of -100 dBm and a 10-bit ADC with 0 dBm of saturation power, the RF receiver's specification is of 51 dB of gain, and 11 dB of noise figure.
Let's now open up the model and verify that the RF receiver chain does meet the budget specifications.
This is a simple model of a communication system. The specs are directly taken from the Zigbee standard. In this test bench, we test the receiver at the minimum power sensitivity level, the transmitted signal with power level set to -100 dbM, and a bandwidth of 2 MHz. The baseband receiver is very simple and is used to recover the OQPSK signal. It uses an AGC and a matched filter.
The RF receiver is modeled with a single amplifier, characterized by the calculated gain and noise figure. The ADC model includes performance characteristics, such as dynamic range, saturation, and the effects of 10-bit quantization. We can validate that the link budget analysis accurately predicts the overall system performance. And with the derived gain and noise figure, we can indeed achieve a chip error rate of approximately 7%.
The very important questions that we need to answer also in this case are how do we partition the gain and noise budget across the different components of the receiver? And what about other effects, such as phase noise, non-linearity, antenna integration. These are exactly the same questions that we had before for the radar receiver.
So how do we get started with RF design? And how do we determine, simultaneously, the architectural RF receiver and the component parameters? An excellent starting point is to use data budget analyzer app. With this app, you can compute cascaded noise figure and power levels, while accounting for component non-linearity and impedance mismatches.
This is not something that is easily done, using spreadsheets and idealized formulas for link analysis. The RF budget analyzer app has been recently enhanced to also include harmonic balance. From the app, we can generate MATLAB scripts to facilitate design space exploration and automation of the analysis process.
Additionally, from the app, you can also generate models for circuit envelope simulation. This allow you to directly compare analysis results obtained with Friis equation or with harmonic balance or with circuit envelope simulation. We can launch data budget analyzer app from the app toolstrip.
First, we set the system parameters. In this case, the receiver operates at 2.45 gigahertz with an input power of minus 100 dBm and a signal bandwidth of two megahertz. Now, we start constructing our chain. We will start with a simple architecture consisting of a bandpass filter, an LNA, a demodulator, a channel filter, and a low-frequency amplification stage. For the bandpass filter, we will use a SAW filter with high out-of-band rejection.
We will use the s-parameters plot to import the Touchstone data file that describes the behavior of the SAW filter. The s-parameters could come from measurement, EM-simulation, or a component data sheet. We plot the s-parameters of this filter over an extended bandwidth.
For the LNA, you set the gain to 20 dB and the noise figure to 4 dB. For the demodulator, we set the gain of 12 dB and the noise figure of 13 dB. We also set the local oscillator frequency to 2.45 gigahertz for a direct down-conversion to 0 hertz.
Since we choose a direct conversion architecture, an IQ demodulator will be used. We add a third-order Butterworth filter, with 40 MHz bandwidth, to select the down-converted signal and suppress the up-converted one. For the low-frequency amplifier, we set the gain equal to 22 dB and a noise figure of 12 dB.
We validate first the system behavior under nominal linear conditions. We will include the components non-linear specifications later. The overall gain of the chain is approximately 51 dB. And it meets the gain specification.
The overall noise figure is 7 dB, well below the budget of 11 dB. This means that we have an SNR of approximately 3.8 dB. This is higher than the minimum required of 0.3 dB, which means that the system will have a chip error rate that is smaller than 7%.
Let's now add the elaborated RF receiver to the test bench and evaluate the resulting chip error rate. We generate the model for circuit envelope simulation directly from the app and embed this model into our test bench, to measure the chip error rate. As you can see, the generated model includes all of the elements of our receiver, including the IQ demodulator.
In our test bench, we can now replace the placeholder for the RF receiver with the model we just generated. When we run this model, we expect the chip error rate to be well below 7%. However, it is much higher. The degraded chip error rate performance is due to the phase rotation introduced by the SAW filter.
The phase offset of the center frequency is approximately minus 419 degrees, that is to say, equal to minus 59 degrees. This phase rotation is not compensated for by the simple baseband receiver, as we have not implemented the mechanism to recover the correct phase of the constellation. We could verify this by plotting the received constellation.
A simple first-order solution is to include a fixed phase rotation to compensate for the SAW filter. We will set the phase rotation to the identified value of 59 degrees. Now if we re-run the simulation, we get a chip error rate around 1%, just as expected. And we have a large margin, so that we can continue to elaborate our design.
The current model does not account for any non-linear behavior. Let's go back to the app and see what happens when we specify second- and third-order non-linear behavior for the respective active components. We added output IP2 and output IP3 specification for the amplifiers and the demodulator in the system.
The results of the budget computed with the Friis equation are the same as before. And we can additionally inspect the results of the IP3 budget analysis. We can correlate the results from the Friis equation against the result obtained with the harmonic balance engine. They are the same, as the receiver is tested at the minimum power sensitivity level, that is to say, in mild non-linear conditions.
But what happens when we increase the input power to the RF chain? Let's now evaluate an edge case, when we increase the input power to -10 dBm. As you can see, the gain is now below 51 dB, as the active component to the receiver is saturated. Also note that output IP2 is quite large. So you might think that this is negligible. We will be able to validate this assumption later on.
Last, we can regenerate the circuit envelope model and use the elaborated RF receiver subsystem in our test bench to verify the system performance under this new operating conditions. Let's now inspect the circuit envelope model more closely. As you can see, the amplifier now includes finite values for IP2 and IP3. Also, the demodulator includes finite values for second- and third-order non-linear behavior.
However, within the circuit envelope model, we can also include additional impairments. For example, we can specify 0.5 dB of IQ gain mismatch.
We can also add local oscillator leakage. For example, let's specify an LO to RF isolation value of 90 dB. Intuitively, you might think that this will have little impact on the system performance. But we will clearly see the effects of reciprocal mixing, as the input power is close to the minimum power sensitivity level.
We can also include the effects of phase noise by specifying a phase noise profile consisting of frequency offsets and a corresponding phase noise levels. You can expect how the demodulator is actually modeled by simply selecting the edit system push button on the block dialog box, or by hovering over the block and right-click your mouse and select look under the mask option.
If we simulate the model, we now see a very high chip error rate and a large spike at DC, resulting from the finite isolation of the local oscillator, used by the demodulator. With such a small input signal, the combination of the finite LO to RF isolation introduces an unintended DC offset that is definitely not negligible.
Let's mitigate this imperfection by including a digital signal processing algorithm for DC offset compensation and rerun the simulation. As compared to a perfectly linear system, the chip error rate has degraded, but is still very good, and is well below the value of the required 7%.
There are a number of different simulation techniques that can be used for RF simulation. The most used one is probably equivalent baseband, where only the interested signal bandwidth is simulated. The simulation is fast. However, the impact of spectral regrowth around harmonics and higher order intermodulation products is ignored.
The other alternative is to simulate in the time domain and proverbially simulate from DC to light, and select time steps based of an integer multiple of the system carrier frequency. This leads to highly accurate simulation of the system, but the trade-off is a simulation that is very time-consuming.
To enable fast and accurate RF system simulation, RF Blockset includes a circuit envelope simulation engine. You can see a circuit envelope as a generalization of equivalent baseband, where you can efficiently simulate a signal with sparse spectral occupation that makes use of multiple carrier frequencies.
RF Blockset is a unique system level simulator, as it allows you to choose which simulation technique to use, and it operates at the behavioral level, rather than at the transistor level, thus further speeding up simulation.
Circuit envelope is not a new technique and it works by combining a transient simulation along with harmonic balance analysis, the same type of analysis that we also use in the RF Budget Analyzer app. The input and the output port allow you to select the envelope's center frequencies. And they simultaneously translate Simulink signals into equivalent into voltages and currents.
By considering all of the harmonics and intermodulation products generated by non-linear behavior, along with interfering signals, you can achieve a more accurate simulation, still sufficiently fast to be used in combination with digital signal processing algorithms.
Let's now see how circuit envelope helps us in modeling our direct conversion receiver. In our RF transceiver, we have used circuit envelope to simulate a baseband signal modulated onto a carrier of 2.45 GHz. We mixed this signal with a local oscillator operating at the same frequency. We make use of a direct down-conversion architecture. And the resulting output signal is centered at 0 hertz.
When we added the finite oscillation in the mixer, a small fraction of the local oscillator power leaked into the RF path and mixed with itself. As a result, a significant DC offset was introduced and we reduced it with a DC blocker.
Let's now go over different use case that is ideally suited for circuit envelope simulation, where the impact of an interfering signal is also included in the system simulation.
And in this model, the RF receiver is identical to the one that we developed at the previous step. We changed the test bench to include an out-of-bound interfering signal. Next to our desired signal, we include a wide-bend interfering signal with 5 MHz of bandwidth. The signal is centered around 2.5 GHz, or 50 MHz away from our signal of interest. And it has much higher power, approximately -30 dBm.
But what the impact is of this interfering signal of an RF receiver? You might remember that the channel select filter has a bandwidth of 40 MHz. So we would expect that the interfering signal to be down-converted to 50 MHz, and to be completely filtered out. However, the resulting chip error rate is much higher than before. So let's investigate this.
To understand the degradation of the chip error rate, we use the same graphics that we used before. And we add an out-of-bound interfering signal and we removed it from the output, as this is outside the bandwidth of the channel select filter.
So why is the chip error rate degraded? The degradation is caused by the finite IP2 of the demodulator. And it propagates through the subsequent stages of the RF system. The desired signal is low-power, so it doesn't excite any non-linearity.
However, the large power of the interfering signal is causing spectral regrowth at DC, effectively decreasing the SNR of the desired signal. This is both simple, but an excellent example, that shows how a behavioral model can help you in understanding the debugging and anticipate the behavior resulting from a combination of intermodulation products and mixer leakage. Even lab testing and full circuit simulation do not allow you to isolate different impairments, understand causes, and mitigate their impact.
In the final example covered in this presentation, I'm going to integrate an antenna into our RF receiver. Every wireless system makes use of one antenna, but it's difficult to include their behavior in system simulation. In this model, we change the input port into a receiving antenna.
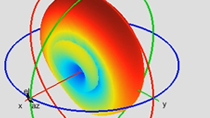
By default, the antenna is isotropic. However, we replace the isotropic antenna with a more realistic microstrip patch antenna, which better describes the physical implementation of the receiver. To achieve this, we make use of full electromagnetic analysis. And to do so, we invoke the Antenna Designer app directly from the antenna block.
We can choose any antenna from the app catalog. In this case, a planar microstrip patch seems appropriate. We design the antenna to be resonant at 2.45 GHz. We analyze the antenna using the method of moments electromagnetic solver. We compute antenna parameters, such as the input impedance and the corresponding one port S-parameters.
We also use the app to compute the far field radiation pattern. In this case, we see that the antenna directivity is 10 dBi. When we run the simulation, the antenna impedance is used to load the SAW filter. Therefore, impedance mismatches are captured in this model. The 3D far field radiation patterns are computed at the nominal carrier frequency and are the frequency of the interfering signal. This allows us to account for direction of arrival.
In this case, we specify the direction of arrival to be 90 degrees of elevation. As a result of the antenna gain, the gain of the first stage can be reduced, while the overall signal to noise ratio performance improves. As we finish up with this last example, I would like to quickly summarize what we covered so far and share some observation how the workflow that we have covered can be used improve the efficiency of RF transceiver design in general.
Do you find yourself to spend too much time repeating the same tasks over and over again? For instance, do you find spreadsheet analysis to be incomplete, time-consuming to develop, and hard to understand? Do you find that the given limitation you need to continuously amend your calculations to include additional effects?
Or maybe you find yourself spending hours validating RFIC adaptive algorithms using overly simplified RF models, for example, validating a DPD algorithms without a realistic power amplifier model, or an AGC (automatic gain control) algorithm without a receiver model, or an adaptive beam-forming algorithm that doesn't included the far-field behavior of the antenna array, or effects like coupling. The lack of integration between RFIC and algorithms leads to over-design and also, to multiple design iterations.
Or maybe you find yourself spending an extensive amount of time debugging a lab prototype. Often, it is not possible to evaluate the full system design until it is tested in the lab. Both building relevant test setups and quality metrics is complicated. And the result is that often, the data measured is analyzed late and it provides limited insight.
And finally, do you find overwhelmingly challenging to communicate with colleagues and customers in a quantifiable way how the RF system is really working? Well, if you recognize any of these challenges, then you will benefit from the workflow that we presented today.
We have seen how the RF budget analyzer can help you analyze and understand and characterize an RF transceiver. The app can be used to construct a more robust RF budget. And the non-linear behavior can be analyzed using harmonic balance.
We have also seen how circuit envelope simulation is an enabler to integrate RF with digital signal processing algorithms, such as those for modeling beamforming, power amplifier linearization, adaptive matching networks, or automatic gain control. The benefit of circuit envelope is that it provides a deeper understanding of the impact of the non-linear effects, of noise generation, and sources of signal distortion, including impedance mismatches.
And finally, we have spanned both system level modeling and electromagnetic domains. And we have seen how to fully integrate an RF transceiver with full-wave EM simulation for an antenna.
With this, I thank you for your attention and invite you to try MATLAB RF Toolbox, RF Blockset, and Antenna Toolbox, and many other MATLAB products in your next RF system design. The examples that we showed today are part of the product examples. So you can just download a trial. Thank you very much for your attention. And if you have questions, please send me an email. Thank you.