Results for
Many MATLAB Cody problems involve solving congruences, modular inverses, Diophantine equations, or simplifying ratios under constraints. A powerful tool for these tasks is the Extended Euclidean Algorithm (EEA), which not only computes the greatest common divisor, gcd(a,b), but also provides integers x and y such that: a*x + b*y = gcd(a,b) - which is Bezout's identity.
Use of the Extended Euclidean Algorithm is very using in solving many different types of MATLAB Cody problems such as:
- Computing modular inverses safely, even for very large numbers
- Solving linear Diophantine equations
- Simplifing fractions or finding nteger coefficients without using symbolic tools
- Avoiding loops (EEA can be implemented recursively)
Below is a recursive implementation of the EEA.
function [g,x,y] = egcd(a,b)
% a*x + b*y = g [gcd(a,b)]
if b == 0
g = a; x = 1; y = 0;
else
[g, x1, y1] = egcd(b, mod(a,b));
x = y1;
y = x1 - floor(a/b)*y1;
end
end
Problem:
Given integers a and m, return the modular inverse of a (mod m).
If the inverse does not exist, return -1.
function inv = modInverse(a,m)
[g,x,~] = egcd(a,m);
if g ~= 1 % inverse doesn't exist
inv = -1;
else
inv = mod(x,m); % Bézout coefficient gives the inverse
end
end
%find the modular inverse of 19 (mod 5)
inv=modInverse(19,5)
When solving Cody problems, sometimes your solution takes too long — especially if you’re recomputing large arrays or iterative sequences every time your function is called.
The Cody work area resets between separate runs of your code, but within one Cody test suite, your function may be called multiple times in a single session.
This is where persistent variables come in handy.
A persistent variable keeps its value between function calls, but only while MATLAB is still running your function suite.
This means:
- You can cache results to avoid recomputation.
- You can accumulate data across multiple calls.
- But it resets when Cody or MATLAB restarts.
Suppose you’re asked to find the n-th Fibonacci number efficiently — Cody may time out if you use recursion naively. Here’s how to use persistent to store computed values:
function f = fibPersistent(n)
import java.math.BigInteger
persistent F
if isempty(F)
F=[BigInteger('0'),BigInteger('1')];
for k=3:10000
F(k)=F(k-1).add(F(k-2));
end
end
% Extend the stored sequence only if needed
while length(F) <= n
F(end+1)=F(end).add(F(end-1));
end
f = char(F(n+1).toString); % since F(1) is really F(0)
end
%calling function 100 times
K=arrayfun(@(x)fibPersistent(x),randi(10000,1,100),'UniformOutput',false);
K(100)
The fzero function can handle extremely messy equations — even those mixing exponentials, trigonometric, and logarithmic terms — provided the function is continuous near the root and you give a reasonable starting point or interval.
It’s ideal for cases like:
- Solving energy balance equations
- Finding intersection points of nonlinear models
- Determining parameters from experimental data
Example: Solving for Equilibrium Temperature in a Heat Radiation-Conduction Model
Suppose a spacecraft component exchanges heat via conduction and radiation with its environment. At steady state, the power generated internally equals the heat lost:
Given constants:
 = 25 W
= 25 W- k = 0.5 W/K
- ϵ = 0.8
- σ = 5.67e−8 W/m²K⁴
- A = 0.1 m²
 = 250 K
= 250 K
Find the steady-state temperature, T.
% Given constants
Qgen = 25;
k = 0.5;
eps = 0.8;
sigma = 5.67e-8;
A = 0.1;
Tinf = 250;
% Define the energy balance equation (set equal to zero)
f = @(T) Qgen - (k*(T - Tinf) + eps*sigma*A*(T.^4 - Tinf^4));
% Plot for a sense of where the root lies before implementing
fplot(f, [250 300]); grid on
xlabel('Temperature (K)'); ylabel('f(T)')
title('Energy Balance: Root corresponds to steady-state temperature')
% Use fzero with an interval that brackets the root
T_eq = fzero(f, [250 300]);
fprintf('Steady-state temperature: %.2f K\n', T_eq);
I set my 3D matrix up with the players in the 3rd dimension. I set up the matrix with: 1) player does not hold the card (-1), player holds the card (1), and unknown holding the card (0). I moved through the turns (-1 and 1) that are fixed first. Then cycled through the conditional turns (0) while checking the cards of each player using the hints provided until it was solved. The key for me in solving several of the tests (11, 17, and 19) was looking at the 1's and 0's being held by each player.
sum(cardState==1,3);%any zeros in this 2D matrix indicate possible cards in the solution
sum(cardState==0,3)>0;%the ones in this 2D matrix indicate the only unknown positions
sum(cardState==1,3)|sum(cardState==0,3)>0;%oring the two together could provide valuable information
Some MATLAB Cody problems prohibit loops (for, while) or conditionals (if, switch, while), forcing creative solutions.
One elegant trick is to use nested functions and recursion to achieve the same logic — while staying within the rules.
Example: Recursive Summation Without Loops or Conditionals
Suppose loops and conditionals are banned, but you need to compute the sum of numbers from 1 to n. This is a simple example and obvisously n*(n+1)/2 would be preferred.
function s = sumRecursive(n)
zero=@(x)0;
s = helper(n); % call nested recursive function
function out = helper(k)
L={zero,@helper};
out = k+L{(k>0)+1}(k-1);
end
end
sumRecursive(10)
- The helper function calls itself until the base case is reached.
- Logical indexing into a cell array (k>0) act as an 'if' replacement.
- MATLAB allows nested functions to share variables and functions (zero), so you can keep state across calls.
Tips:
- Replace 'if' with logical indexing into a cell array.
- Replace for/while with recursion.
- Nested functions are local and can access outer variables, avoiding global state.
Many MATLAB Cody problems involve recognizing integer sequences.
If a sequence looks familiar but you can’t quite place it, the On-Line Encyclopedia of Integer Sequences (OEIS) can be your best friend.
OEIS will often identify the sequence, provide a formula, recurrence relation, or even direct MATLAB-compatible pseudocode.
Example: Recognizing a Cody Sequence
Suppose you encounter this sequence in a Cody problem:
1, 1, 2, 3, 5, 8, 13, 21, ...
Entering it on OEIS yields A000045 – The Fibonacci Numbers, defined by:
F(n) = F(n-1) + F(n-2), with F(1)=1, F(2)=1
You can then directly implement it in MATLAB:
function F = fibSeq(n)
F = zeros(1,n);
F(1:2) = 1;
for k = 3:n
F(k) = F(k-1) + F(k-2);
end
end
fibSeq(15)
When solving MATLAB Cody problems involving very large integers (e.g., factorials, Fibonacci numbers, or modular arithmetic), you might exceed MATLAB’s built-in numeric limits.
To overcome this, you can use Java’s java.math.BigInteger directly within MATLAB — it’s fast, exact, and often accepted by Cody if you convert the final result to a numeric or string form.
Below is an example of using it to find large factorials.
function s = bigFactorial(n)
import java.math.BigInteger
f = BigInteger('1');
for k = 2:n
f = f.multiply(BigInteger(num2str(k)));
end
s = char(f.toString); % Return as string to avoid overflow
end
bigFactorial(100)
Run MATLAB using AI applications by leveraging MCP. This MCP server for MATLAB supports a wide range of coding agents like Claude Code and Visual Studio Code.
Check it out and share your experiences below. Have fun!
GitHub repo: https://github.com/matlab/matlab-mcp-core-server
Yann Debray's blog post: https://blogs.mathworks.com/deep-learning/2025/11/03/releasing-the-matlab-mcp-core-server-on-github/
We are excited to announce the first edition of the MathWorks AI Challenge. You’re invited to submit innovative solutions to challenges in the field of artificial intelligence. Choose a project from our curated list and submit your solution for a chance to win up to $1,000 (USD). Showcase your creativity and contribute to the advancement of AI technology.
Watch episodes 5-7 for the new stuff, but the whole series is really great.
Local large language models (LLMs), such as llama, phi3, and mistral, are now available in the Large Language Models (LLMs) with MATLAB repository through Ollama™!
Read about it here:
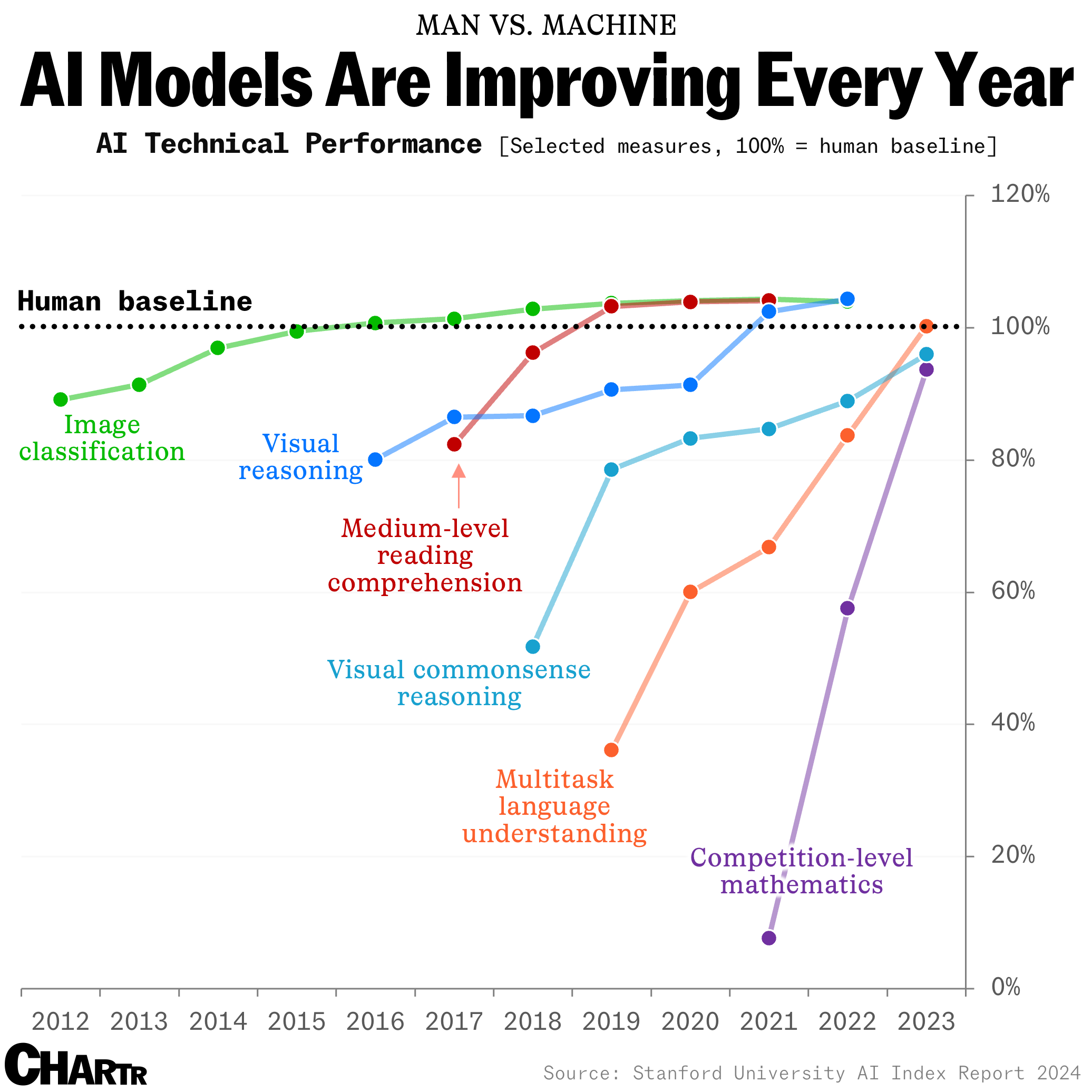
How long until the 'dumbest' models are smarter than your average person? Thanks for sharing this article @Adam Danz
I was in a meeting the other day and a coworker shared a smiley face they created using the AI Chat Playground. The image looked something like this:

And I suspect the prompt they used was something like this:
"Create a smiley face"
I imagine this output wasn't what my coworker had expected so he was left thinking that this was as good as it gets without manually editing the code, and that the AI Chat Playground couldn't do any better.
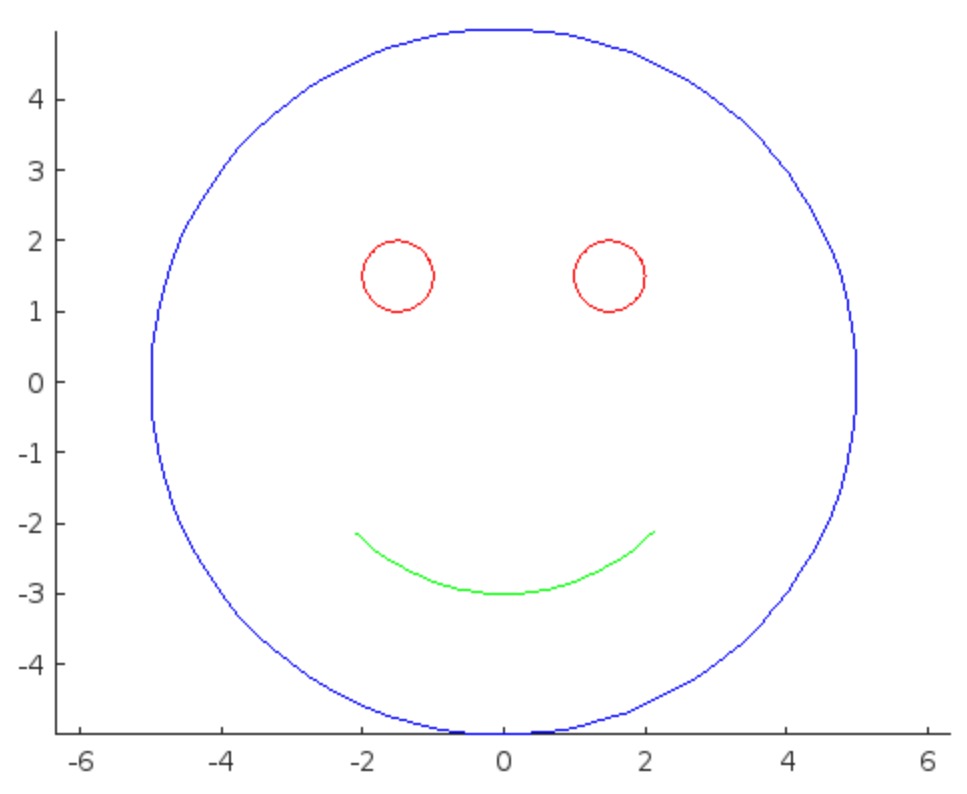
I thought I could get a better result using the Playground so I tried a more detailed prompt using a multi-step technique like this:
"Follow these instructions:
- Create code that plots a circle
- Create two smaller circles as eyes within the first circle
- Create an arc that looks like a smile in the lower part of the first circle"
The output of this prompt was better in my opinion.
These queries/prompts are examples of 'zero-shot' prompts, the expectation being a good result with just one query. As opposed to a back-and-forth chat session working towards a desired outcome.
I wonder how many attempts everyone tries before they decide they can't anything more from the AI/LLM. There are times I'll send dozens of chat queries if I feel like I'm getting close to my goal, while other times I'll try just one or two. One thing I always find useful is seeing how others interact with AI models, which is what inspired me to share this.
Does anyone have examples of techniques that work well? I find multi-step instructions often produces good results.
Unlike last year's contest, there are some new technologies this year that might offer some advantages. Namely generative AI's like ChatGPT, Bard, etc. Not to be excluded, MathWorks just launched the AI Chat Playground :)
The contest development team has identified an issue when trying to link your new entries to submissions in the File Exchange. The issue has prevented some users from successfully linking their entries. We have a fix and will be deploying it today at 3pm EST.
