Root Locus For A PID Controller
Hello,
I have an Open Loop Transfer Function:
Gc(s)Gp(s) = aKp(1+Tis) / Tis(s+1+p)
It was decided for this system a=5, Ti=0.1 and p=0.5
What would the poles and zeroes be for this?
Ive done the other examples but this one looks very different to the other questions and it has me stuck.
Any help is appreciated and sorry if this is the wrong place to post such questions.
2 Comments
Time Descendingto determine the poles and zeroes of the given open loop transfer function, we need to first simplify it by cancelling out the common factors.
Gc(s)Gp(s) = aKp(1+Tis) / Tis(s+1+p)
Gc(s)Gp(s) = aKp / (s+1+p)
Jonathan,
The transfer functions are clear:
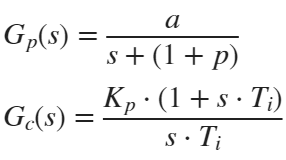
For 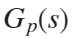 :
:
zeros: none
poles: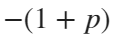
For 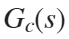 :
:
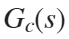 :
: zeros: 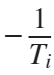
poles:
Although it's optional, you may use MATLAB to do this as well:
%% TF for uncompensated system
% plant parameters
a = 5;
Ti = 0.1;
p = 0.5;
% transfer function for plant
Gp = tf([a],[1 (1+p)]);
sys_uncompensated = Gp
[z,p,k] = tf2zp([a],[1 (1+p)])
%% Root locus for Uncompensated System
figure(1);
rlocus(sys_uncompensated);
title('Root locus for uncompensated system');
grid;
figure(2);
pzmap(sys_uncompensated);
grid;
title('Pole Zero map for uncompensated system');
%% TF for PI controller system
Kp = 10; % gain for PI controlller, Kc = Kp
Ti = 0.1; % time const for PI controller, Ti = Kp/Ki
num_comp = (Kp)*[Ti 1];
den_comp = [Ti 0];
figure(3);
tf_comp = tf(num_comp,den_comp); % TF for PI controller
[z,p,k] = tf2zp(num_comp,den_comp)
rlocus(tf_comp);
title('Root locus for PI controller system');
grid;
figure(4);
pzmap(tf_comp);
title('Pole Zero map for PI controller system');
grid;
%% TF for Compensated system
sys_compensated = tf_comp*sys_uncompensated
sys_closed_loop_compensated = feedback(sys_compensated,1);
figure(5);
pzmap(sys_closed_loop_compensated)
title('Pole Zero map for compensated system');
grid;
Hope this helps.
Have a good day!
Sign in to participate