Orthogonal and Biorthogonal Filter Banks
This example shows to construct and use orthogonal and biorthogonal filter banks. The classic critically sampled two-channel filter bank is shown in this figure.
Let and denote the lowpass and highpass analysis filters and and denote the corresponding lowpass and highpass synthesis filters. A two-channel critically sampled filter bank filters the input signal using a lowpass and highpass filter. The subband outputs of the filters are downsampled by two to preserve the overall number of samples. To reconstruct the input, upsample by two and then interpolate the results using the lowpass and highpass synthesis filters. If the filters satisfy certain properties, you can achieve perfect reconstruction of the input.
To demonstrate this, filter an ECG signal using Daubechies's extremal phase wavelet with two vanishing moments. The example explains the notion of vanishing moments in a later section. Load and plot the signal.
load wecg plot(wecg) title("ECG Signal") axis tight

For this example, use dwtmode to set the padding mode for the discrete wavelet transform (DWT) to periodization. This does not extend the signal.
origmodestatus = dwtmode("status","nodisplay"); dwtmode("per","nodisplay");
Orthogonal Wavelet Filters
Obtain the lowpass (scaling) and highpass (wavelet) analysis and synthesis filters of wavelet.
[gtilde,htilde,g,h] = wfilters("db2");The analysis and synthesis filters for the "db2" wavelet are just time reverses of each other. This is the case with all orthogonal wavelet filter banks. You can see this by comparing the following.
scalingFilters = [flip(gtilde); g]
scalingFilters = 2×4
0.4830 0.8365 0.2241 -0.1294
0.4830 0.8365 0.2241 -0.1294
waveletFilters = [flip(htilde); h]
waveletFilters = 2×4
-0.1294 -0.2241 0.8365 -0.4830
-0.1294 -0.2241 0.8365 -0.4830
Implement Single-Level Two-Channel Filter Bank Using dwt
Obtain the level-one DWT of the ECG signal. This is equivalent to the analysis branch (with downsampling) of the two-channel filter bank in the figure at the start of this example.
[lowpass,highpass] = dwt(wecg,gtilde,htilde);
Upsample and interpolate the lowpass (scaling coefficients) and highpass (wavelet coefficients) subbands with the synthesis filters and demonstrate perfect reconstruction.
xrec = idwt(lowpass,highpass,g,h); max(abs(wecg-xrec))
ans = 1.3658e-12
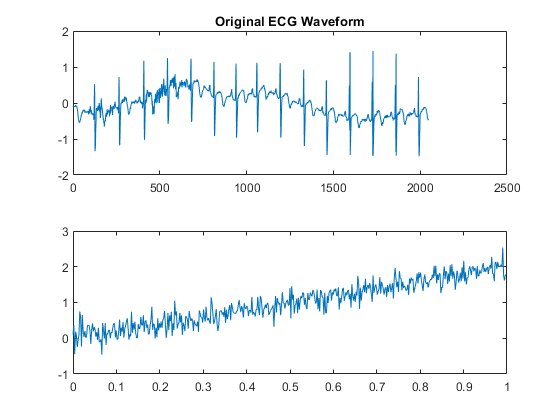
tiledlayout(2,1) nexttile plot(wecg) axis tight title("Original ECG Waveform") nexttile plot(xrec) axis tight title("Reconstructed ECG Waveform")
Instead of providing dwt with the filters in the previous example, use the string "db2" instead. Using the wavelet family short name, "db", and filter number, 2, you do not have to specify the analysis and synthesis filters.
[lowpass,highpass] = dwt(wecg,"db2"); xrec = idwt(lowpass,highpass,"db2");
The filter number in the Daubechies's extremal phase and least asymmetric phase wavelets ("db" and "sym") refers to the number of vanishing moments. Basically, a wavelet with N vanishing moments removes a polynomial of order N-1 in the wavelet coefficients. To illustrate this, construct a signal which consists of a linear trend with additive noise.
figure n = (0:511)/512; x = 2*n+0.2*randn(size(n)); plot(n,x)
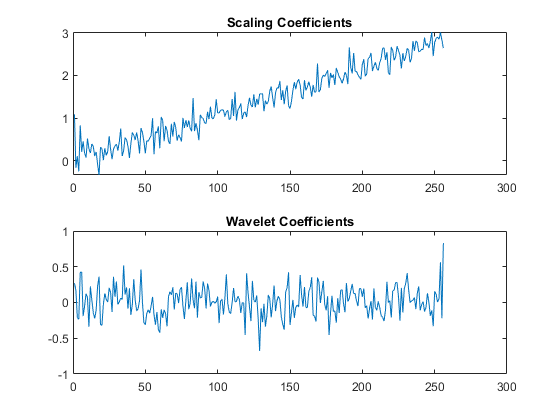
A linear trend is a polynomial of degree 1. Therefore, a wavelet with two vanishing moments removes this polynomial. The linear trend is preserved in the scaling coefficients and the wavelet coefficients can be regarded as consisting of only noise. Obtain the level-one DWT of the signal with the "db2" wavelet (two vanishing moments) and plot the coefficients.
[A,D] = dwt(x,'db2'); figure tiledlayout(2,1) nexttile plot(A) axis tight title("Scaling Coefficients") nexttile plot(D) axis tight title("Wavelet Coefficients")

Implement Multilevel Two-Channel Filter Bank Using wavedec
You can use dwt and idwt to implement a two-channel orthogonal filter bank, but it is often more convenient to implement a multi-level two-channel filter bank using wavedec. The multi-level DWT iterates on the output of the lowpass (scaling) filter. In other words, the input to the second level of the filter bank is the output of the lowpass filter at level 1. A two-level wavelet filter bank is illustrated in this figure.
At each successive level, the number of scaling and wavelet coefficients is downsampled by two so the total number of coefficients are preserved. Obtain the level three DWT of the ECG signal using the "sym4" orthogonal filter bank.
[C,L] = wavedec(wecg,3,"sym4");The number of coefficients by level is contained in the vector, L. The first element of L is 256, which represents the number of scaling coefficients at level 3 (the final level). The second element of L is the number of wavelet coefficients at level 3. Subsequent elements give the number of wavelet coefficients at higher levels until you reach the final element of L. The final element of L is equal to the number of samples in the original signal. The scaling and wavelet coefficients are stored in the vector C in the same order. To extract the scaling or wavelet coefficients, use appcoef or detcoef. Extract all the wavelet coefficients in a cell array and final-level scaling coefficients.
wavcoefs = detcoef(C,L,"dcells"); a3 = appcoef(C,L,"sym4");
You can plot the wavelet and scaling coefficients at their approximate positions.
cfsmatrix = zeros(numel(wecg),4);
cfsmatrix(1:2:end,1) = wavcoefs{1};
cfsmatrix(1:4:end,2) = wavcoefs{2};
cfsmatrix(1:8:end,3) = wavcoefs{3};
cfsmatrix(1:8:end,4) = a3;
figure
tiledlayout(5,1)
nexttile
plot(wecg)
title("Original Signal")
axis tight
for kk = 2:4
nexttile
stem(cfsmatrix(:,kk-1), ...
marker="none",ShowBaseLine="off")
ylabel("D"+num2str(kk-1))
axis tight
end
nexttile
stem(cfsmatrix(:,end), ...
marker="none", ...
ShowBaseLine="off")
ylabel("A3")
xlabel("Sample")
axis tight
Because the critically sampled wavelet filter bank downsamples the data at each level, the analysis must stop when you have only one coefficient left. In the case of the ECG signal with 2048 samples, this must occur when .
[C,L] = wavedec(wecg,log2(numel(wecg)),"sym4"); fprintf("The number of coefficients at the final level is %d. \n",L(1));
The number of coefficients at the final level is 1.
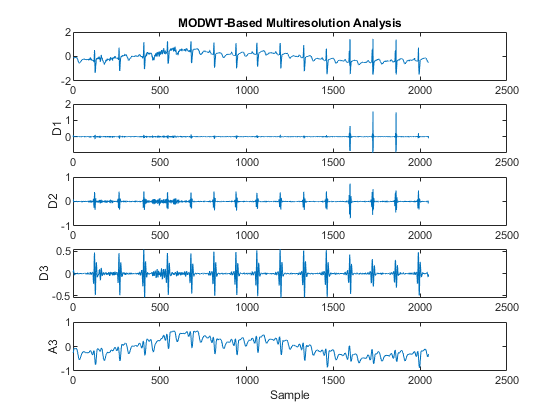
If you wish to implement an orthogonal wavelet filter bank without downsampling, you can use modwt.
ecgmodwt = modwt(wecg,"sym4",3); ecgmra = modwtmra(ecgmodwt,"sym4"); figure t=tiledlayout(5,1); nexttile plot(wecg) axis tight title("Original Signal") for kk = 2:4 nexttile plot(ecgmra(kk-1,:)) axis tight ylabel("D"+num2str(kk-1)) end nexttile plot(ecgmra(end,:)) axis tight ylabel("A3") xlabel("Sample") title(t,"MODWT-Based Multiresolution Analysis")
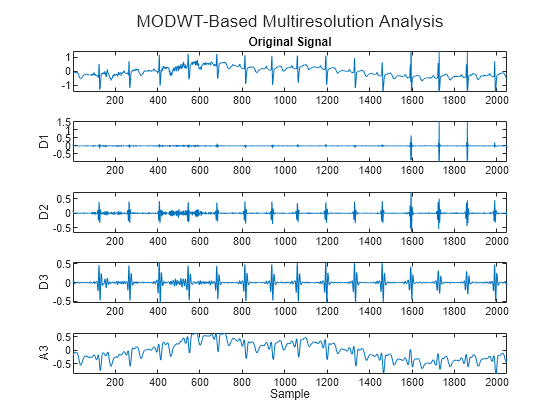
Biorthogonal Wavelet Filters
In a biorthogonal filter bank, the synthesis filters are not simply time-reversed versions of the analysis filters. The family of biorthogonal spline wavelet filters are an example of such filter banks.
[LoD,HiD,LoR,HiR] = wfilters("bior3.5");If you examine the analysis filters (LoD, HiD) and the synthesis filters (LoR, HiR), you see that they are very different. These filter banks still provide perfect reconstruction.
[A,D] = dwt(wecg,LoD,HiD); xrec = idwt(A,D,LoR,HiR); max(abs(wecg-xrec))
ans = 4.4409e-16
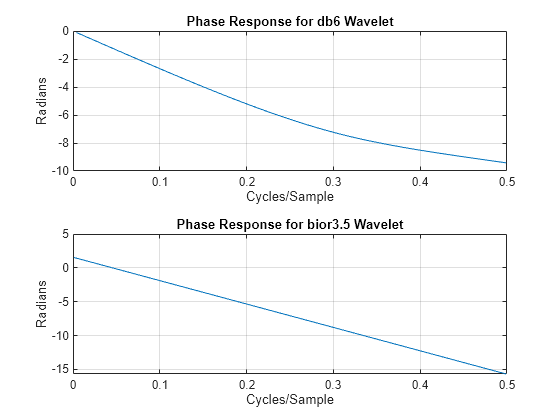
Biorthogonal filters are useful when linear phase is a requirement for your filter bank. Orthogonal filters cannot have linear phase with the exception of the Haar wavelet filter. If you have Signal Processing Toolbox™, you can look at the phase responses for an orthogonal and biorthogonal pair of wavelet filters.
[Lodb6,Hidb6] = wfilters("db6"); [PHIdb6,W] = phasez(Hidb6,1,512); PHIbior35 = phasez(HiD,1,512); figure tiledlayout(2,1) nexttile plot(W./(2*pi),PHIdb6) title("Phase Response for db6 Wavelet") grid on xlabel("Cycles/Sample") ylabel("Radians") nexttile plot(W./(2*pi),PHIbior35) title("Phase Response for bior3.5 Wavelet") grid on xlabel("Cycles/Sample") ylabel("Radians")
Set the padding mode back to the original setting.
dwtmode(origmodestatus,"nodisplay")