3-D Motion Reconstruction Using Multiple Cameras

Since R2025a

This example shows how to reconstruct 3-D motion of an object for use in a motion capture system that contains of multiple cameras.

Overview

Motion capture systems record the 3-D motion of objects to capture precise movements and translate them into digital models. These models can then be used to animate digital characters in films, video games, and virtual reality. These models can also be used to help design robotic systems to mimic human or animal movements. For example, the African Robotics Unit (ARU) uses motion capture systems to study how cheetahs move, to build more agile robots. In one of their projects, they place a cheetah in a pickup truck with cameras mounted inside the truck. As the truck moves, the cameras record footage to later reconstruct and analyze the cheetah's 3-D movements as shown below.

This example uses this data set from ARU, which includes images captured by four cameras, to reconstruct the motion of a cheetah. You first calibrate the multi-camera system to estimate the poses of the cameras relative to each other. Then you use the estimated relative poses to reconstruct the 3-D motion of the cheetah.

Calibrate the Multi-Camera System

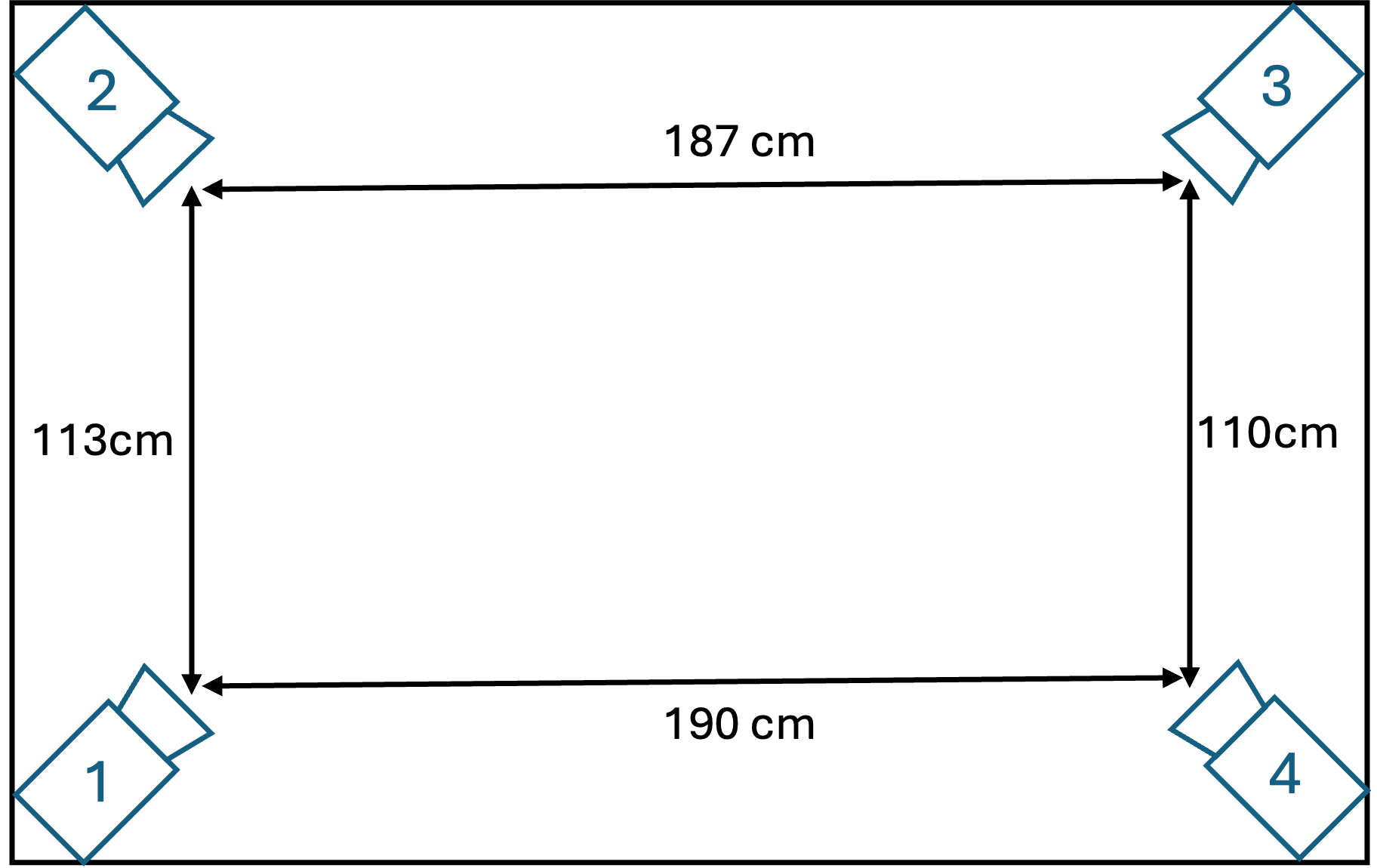
The multi-camera system uses four GoPro Hero12 cameras mounted on four corners of the pickup truck as show below.

Estimating the relative poses of the four cameras using multi-camera calibration consists of two steps:

1. Estimate camera intrinsic parameters.

2. Estimate camera extrinsic parameters.

Estimate Camera Intrinsic Parameters

Estimate the intrinsic parameters of each camera to remove image distortion and to determine the relative camera poses. In this example, the four cameras were individually calibrated with a checkerboard calibration pattern Using the Single Camera Calibrator App, and the four fisheyeIntrinsics objects were saved to four-gopro-intrinsics.mat.

Load these estimated camera intrinsic parameters.

goproParams = load("four-gopro-intrinsics.mat");
intrinsics = goproParams.intrinsics;

Estimate Camera Extrinsic Parameters

Estimating the extrinsics requires capturing a calibration pattern from the four cameras in different orientations such that at least two cameras see the pattern at the same time. In this example, a 7-by-10 checkerboard pattern is used for calibration.

Load Calibration Data

Download the data set.

datasetDir = helperDownloadDataset(pwd);

Downloading calibration images (166 MB)...

The data set has calibration files that contain fisheye images which were corrected for lens disortion using undistortFisheyeImage. In addition to camera intrinsics, the four-gopro-intrinsics.mat file contains their virtual pinhole camera parameters as created by undistortFisheyeImage. Load these parameters into MATLAB.

virtualIntrinsics = goproParams.virtualIntrinsics;

Undistorted calibration images are used in this example for faster runtime performance. However, you can also use raw calibration images and fisheye intrinsics for multi-camera calibration.

Perform Multi-Camera Calibration

Estimate relative poses of the cameras using multi-camera calibration through these steps.

1. Detect calibration pattern keypoints using detectPatternPoints.

2. Generate pattern world points using patternWorldPoints.

3. Estimate relative camera poses using estimateMultiCameraParameters.

Specify calibration image filenames for each camera.

numCameras = 4;
camDirPrefix = fullfile(datasetDir,"calib-images","Cam");
imageFiles = cell(1,numCameras);
for i = 1:numCameras
    imds = imageDatastore(camDirPrefix+i);
    imageFiles{i} = imds.Files;
end

Display few calibration images.

figure
montage(imageFiles{1},Size=[2,2])

To calibrate multiple cameras, the calibration data set must contain multiple views of the pattern in different orientations relative to the cameras. In multi-camera calibration, a view is a single capture of the pattern from all cameras simultaneously.

In this example, to simplify data collection, images were taken with two cameras turned on while the other two were turned off. This resulted in missing images from two cameras in every view. To identify missing images, use the frame number in the filename and fill the corresponding file names with empty strings.

imageFileNames = helperFillMissingViews(imageFiles);

Detect the checkerboard keypoints from the calibration images.

patternDims = [7,10];
imagePoints = detectPatternPoints(imageFileNames,"checkerboard",patternDims);

[==================================================] 100%
Elapsed time: 00:01:05
Estimated time remaining: 00:00:00

Visualize the detected keypoints in one of the images.

camIndex = 2;
viewIndex = 10;
figure
imshow(imageFileNames(viewIndex,camIndex))
hold on
plot(imagePoints(:,1,viewIndex,camIndex),imagePoints(:,2,viewIndex,camIndex),"gx");

Generate the world coordinates of the checkerboard keypoints in the pattern-centric coordinate system, with the upper-left corner at (0,0).

squareSize = 4; % in centimeters
worldPoints = patternWorldPoints("checkerboard",patternDims,squareSize);

In this example, calibration is performed using the undistorted images. Use the virtual intrinsics to perform multi-camera calibration using the estimateMultiCameraParameters function.

params = estimateMultiCameraParameters(imagePoints,worldPoints,virtualIntrinsics,WorldUnits="cm")

params = 
  multiCameraParameters with properties:

   Extrinsic Parameters
                       CameraPoses: [4×1 rigidtform3d]
              ReferenceCameraIndex: 1
                        NumCameras: 4

   Intrinsic Parameters
                        Intrinsics: {4×1 cell}

   Accuracy of Estimation
             MeanReprojectionError: 2.4891
    MeanReprojectionErrorPerCamera: [4×1 double]

   Calibration Settings
                          NumViews: 23
                CovisibilityMatrix: [4×4 logical]
                       WorldPoints: [54×2 double]
                        WorldUnits: "cm"

The result is a multiCameraParameters object, which includes the camera poses relative to a reference camera in its CameraPoses property. The reference camera is indicated by the ReferenceCameraIndex property which is the first camera by default. To set a different reference camera, use the ReferenceCameraIndex name-value argument of the estimateMultiCameraParameters function.

Evaluate Extrinsic Calibration Results

Use showExtrinsics to visualize the position of the patterns relative to the cameras.

• Verify that the patterns are in their expected locations.

• Ensure that the patterns are neither too far from nor too close to the cameras.

• Confirm that the patterns are not positioned behind the cameras.

figure
showExtrinsics(params)
view(2)

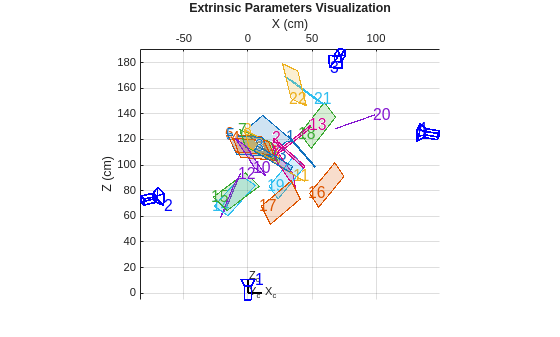
This plot also displays the cameras' relative positions, reflecting their arrangement at the four corners of the pickup truck, as shown earlier.

Use showReprojectionErrors to visualize the average reprojection error in each calibration image across views and cameras.

figure(Position=[100, 100, 1000, 400])
showReprojectionErrors(params)

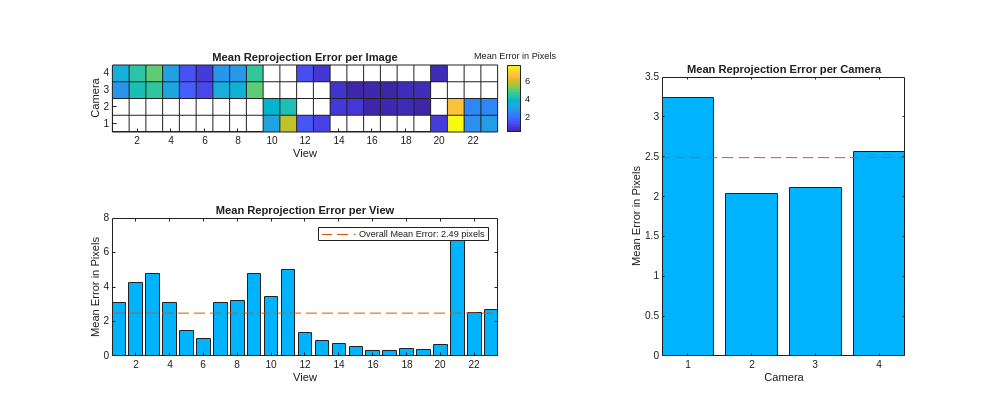
As a general rule, the mean reprojection error should be as small as possible, ideally under 1 pixel, to ensure high calibration accuracy. For most applications, a mean reprojection error of around 1-2 pixels may also be acceptable based on the application requirements. If the overall mean reprojection error is too high (greater than 5 pixels), consider excluding the images with the highest errors and then recalibrating. Use the Mean Reprojection Error per View plot to identify the views contributing most to the errors, and the Mean Reprojection Error per Image plot to pinpoint the problematic images among the different views.

Note that recalibrating cameras to reduce reprojection errors can sometime lead to inaccurate calibration. This is because the images used in the recalibration may capture the pattern in a similar pose relative to the camera. In such scenarios, it is useful to add a sanity check by comparing the results against manual measurements made using a physical measurement device. If necessary, you can capture additional high quality calibration images to compensate for the removal of images with high reprojection errors.

To verify calibration accuracy, compute the distances between adjacent cameras and compare against the manual measurements.

% Get relative locations of the cameras with respect to the reference
% camera (which is camera 1 in this example).
camPoses = params.CameraPoses;
cam1 = camPoses(1).Translation;
cam2 = camPoses(2).Translation;
cam3 = camPoses(3).Translation;
cam4 = camPoses(4).Translation; 
estimates = [norm(cam2-cam1), norm(cam3-cam2), norm(cam4-cam3), norm(cam4-cam1)];

measurements = [113, 187, 110, 190]; % in centimeters.
diff = rmse(measurements, estimates);
disp("Difference between manual measurements and calibration estimates is " + diff + " centimeters")

Difference between manual measurements and calibration estimates is 1.8371 centimeters

Note that the manual measurements were made from center of one camera casing to the center of another camera casing. However, the calibration estimates provide the precise distance between the optical centers of two cameras which cannot be measured manually. Given that the GoPro Hero12 camera thickness is 3.36 cm, the estimated calibration extrinsics are within reasonable tolerances.

Reconstruct 3-D Motion

To reconstruct the 3-D motion of a cheetah from the videos, follow these steps for each frame.

1. Label 2-D keypoints of the cheetah.

2. Undistort the detected keypoints using the camera intrinsics.

3. Triangulate 3-D keypoint locations based on 2-D keypoints from multiple views.

Load the recorded footage from the four cameras containing the cheetah and play the four videos.

% Construct VideoReader objects for the footage from each camera to read them.
videoFiles = fullfile(datasetDir,"sample-videos","Cam") + (1:numCameras) + ".avi";
readers = cell(4,1);
for i = 1:numCameras
    readers{i} = VideoReader(videoFiles(i));
end

% Display the videos.
numFrames = readers{i}.NumFrames;
I = cell(numCameras,1);
figure
for frameIndex = 1:numFrames
    for j = 1:numCameras
        I{j} = readers{j}.read(frameIndex);
    end
    montage(I)
    drawnow limitrate
end

clear readers

Undistort Cheetah Keypoints in Images

Each frame of these recordings includes 20 keypoints on the cheetah, automatically annotated using DeepLabCut [1][2]. These keypoints encompass the tail, legs, hips, spine, shoulders, neck, ears, eyes, and nose. Load these annotated labels into the MATLAB workspace.

annotations = load("cheetah-labels.mat");
labels = annotations.labels;
numKeypoints = 20;

labels is a numKeypoints-by-2-by-numFrames-numCameras vector containing the cheetah keypoints. If a camera does not see a keypoint in a frame, it is marked with a NaN.

Undistort the annotated keypoints using undistortFisheyePoints and the fisheye intrinsics of the corresponding camera.

keypoints = nan(size(labels));
for i = 1:numCameras
    
    % Reshape the labels [numKeypoints*numFrames, 2] to process all frames at once.
    reshapedLabels = permute(labels(:,:,:,i),[1,3,2]);  % [numKeypoints, numFrames, 2]
    reshapedLabels = reshape(reshapedLabels,numKeypoints*numFrames,2);  % [numKeypoints*numFrames, 2]
    
    % Undistort all points in batch.
    undistortedPoints = undistortFisheyePoints(reshapedLabels,intrinsics(i));
    
    % Reshape the undistorted points back to [numKeypoints, 2, numFrames].
    undistortedPoints = reshape(undistortedPoints,numKeypoints,numFrames,2);
    keypoints(:,:,:,i) = permute(undistortedPoints,[1,3,2]);  % [numKeypoints, 2, numFrames]
end

Estimate 3-D Locations of 2-D Keypoints

Reconstruct the cheetah motion by transforming the undistorted 2-D keypoints to 3-D keypoints using triangulateMultiview. To perform the reconstruction for every keypoint in every frame:

1. Verify whether at least two cameras see the keypoint.

2. Identify the cameras that see the keypoint.

3. Construct a pointTrack object with the corresponding keypoints in all the cameras.

4. Estimate 3-D locations of the 2-D keypoints using triangulateMultiview.

xyzPoints = nan(numKeypoints,3,numFrames);
for frameIndex = 1:numFrames

    % Extract keypoints for the frame.
    pts = squeeze(keypoints(:,:,frameIndex,:));

    visiblePts = ~isnan(pts);
    for pointIndex = 1:numKeypoints
        % Get the visibility of i-th keypoint in all cameras.
        visibility = all(visiblePts(pointIndex,:,:),2);

        % Verify whether at least two cameras see the keypoint.
        if sum(visibility) >= 2

            % Identify the cameras that see the keypoint.
            idx = uint32(find(visibility));

            % Extract the corresponding camera poses.
            poses = table(idx,camPoses(idx),...
                VariableNames=["ViewId","AbsolutePose"]);
            
            % Construct a pointTrack object to reconstruct the i-th keypoint
            % using its image coordinates from all cameras that are seeing it.
            matchedPts = squeeze(pts(pointIndex,:,idx))';
            pt = pointTrack(idx,matchedPts);
            
            % Estimate 3-D locations of the 2-D keypoints using triangulateMultiview.
            [result,~,valid] = triangulateMultiview(pt,poses,virtualIntrinsics(idx));

            % Store valid results.
            if valid
                xyzPoints(pointIndex,:,frameIndex) = result;
            end
        end
    end
end

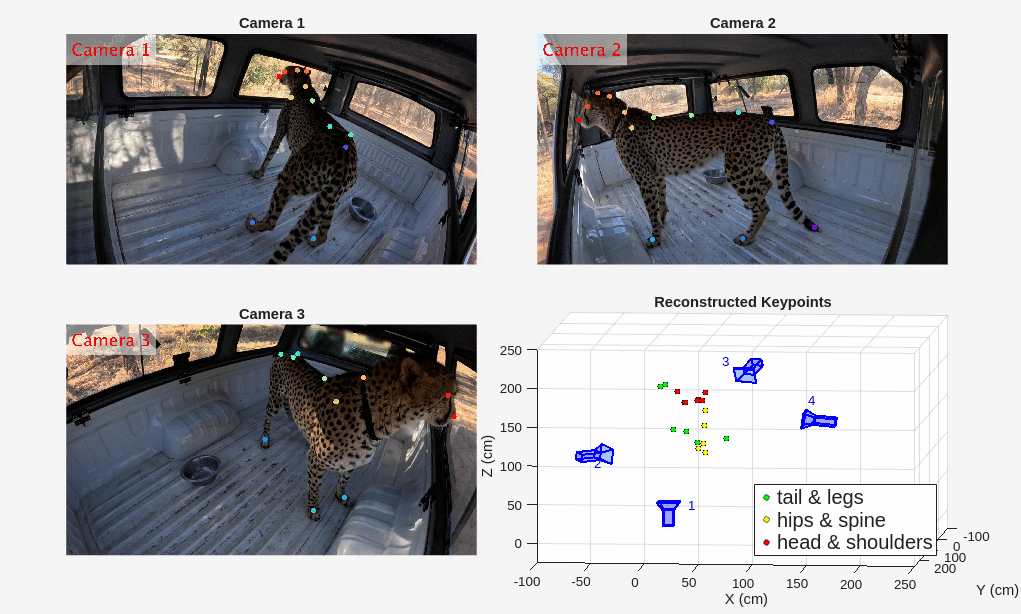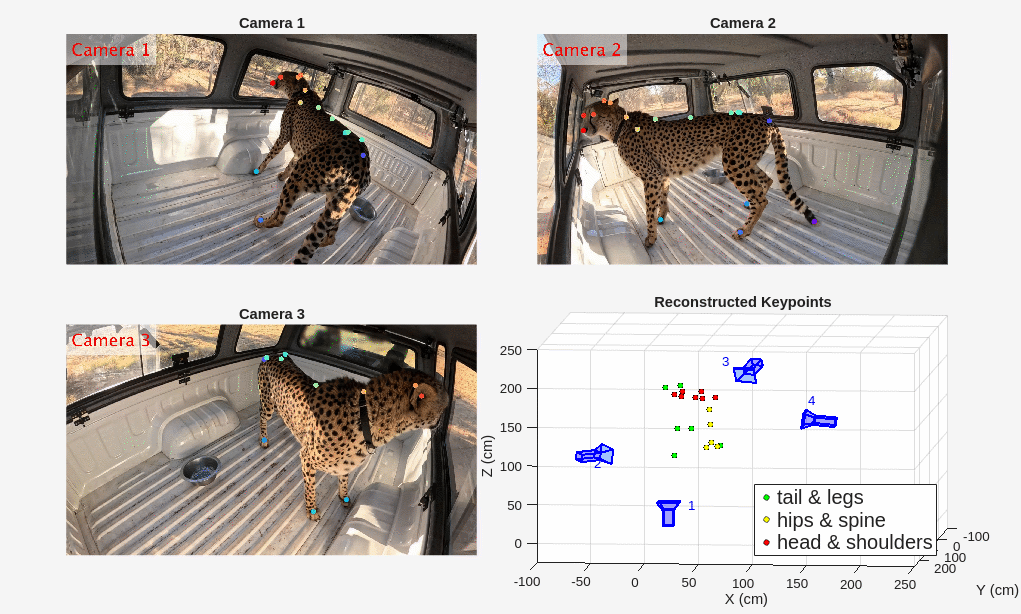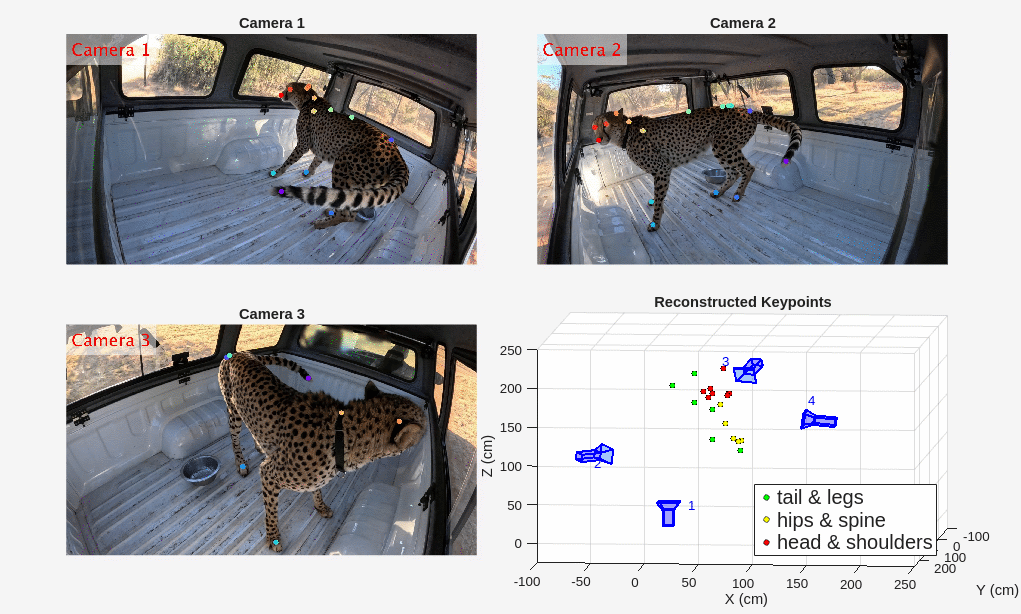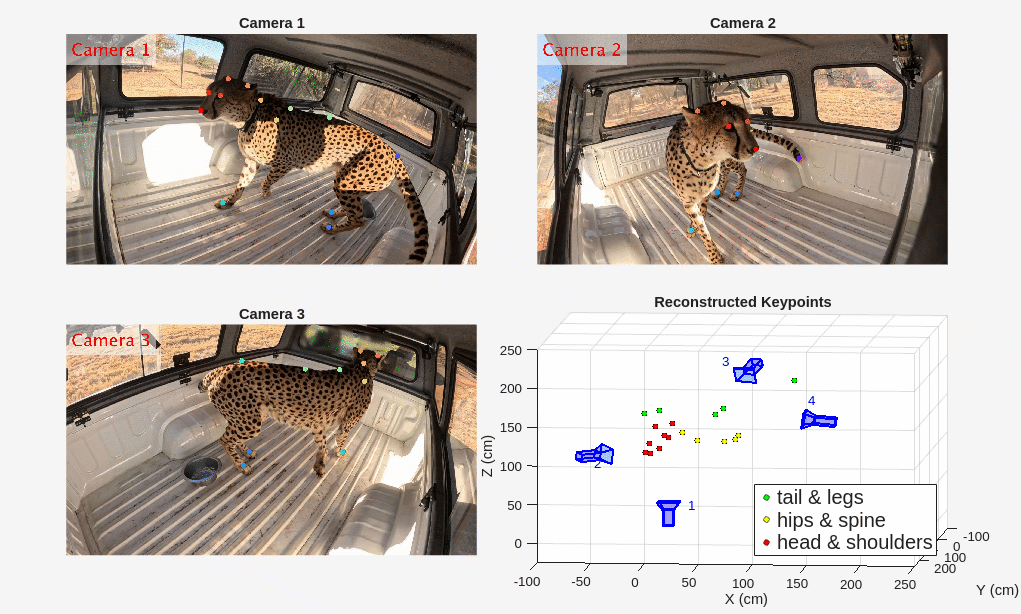
Visualize 3-D Motion

Display the reconstructed motion using the helper function helperShowReconstructedPoints along with the videos from three cameras. The helper function plots the 3-D cheetah keypoints in three groups: tails and legs, hips and spine, and head and shoulders.

figure
helperShowReconstructedPoints(xyzPoints,camPoses,videoFiles);

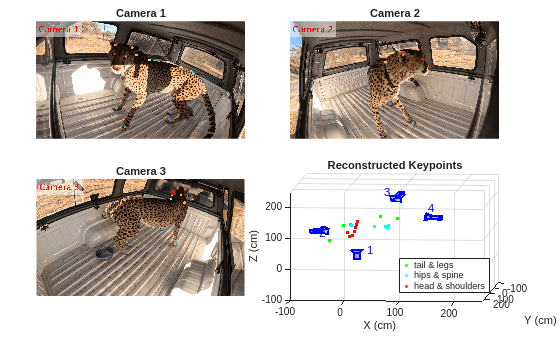
The reconstructed motion of the head matches with the video footages as the cheetah moves from camera 3 in the beginning of the video to camera 2 at the end.

Summary

This example shows how to calibrate multiple cameras and use them to reconstruct 3-D motion of an object. You can use the methods in this example with different camera configurations in which the camera views overlap.

Data Set Credits

The data set for this example was provided by Amir Patel, Stacey Shield, and Kamryn Norton from University of Cape Town.

References

[1] Mathis, A., Mamidanna, P., Cury, K. M. , Abe, T., Murthy, V. N., Mathis, M. W., and Bethge, M. "DeepLabCut: markerless pose estimation of user-defined body parts with deep learning", Nature Neuroscience 21, 1281-1289, 2018.

[2] Nath, T., Mathis, A., Chen, A. C., Patel, A., Bethge, M., and Mathis, M. W. "Using DeepLabCut for 3D markerless pose estimation across species and behaviors", Nature Protocols 14, 2152-2176, 2019.

Supporting Functions

helperDownloadDataset

The helperDownloadDataset function downloads example data set.

function datasetDir = helperDownloadDataset(downloadFolder)

    url = "https://www.mathworks.com/supportfiles/vision/data/cheetah-dataset.zip";
    zipFile = fullfile(downloadFolder,"cheetah-dataset.zip");
    datasetDir = fullfile(downloadFolder,"cheetah-dataset");

    % Download data set.
    if ~exist(zipFile,"file") && ~exist(datasetDir,"dir")
        disp("Downloading calibration images (166 MB)...")
        websave(zipFile,url);
    end

    % Unzip data set.
    if ~exist(datasetDir,"dir")
        unzip(zipFile,pwd)
    end
end

helperFillMissingViews

The helperFillMissingViews function fills missing image filenames with empty filenames.

function filledImageFiles = helperFillMissingViews(imageFiles)
  
    % Extract all unique view identifiers from all cameras.
    allViewIdentifiers = [];
    for i = 1:numel(imageFiles)
        % Extract view identifiers from filenames.
        viewIdentifiers = helperExtractViewIdentifiers(imageFiles{i});
        allViewIdentifiers = union(allViewIdentifiers,viewIdentifiers);
    end
      
    % Initialize the filled image files cell array.
    filledImageFiles = cell(size(imageFiles));
      
    % Fill missing views with empty strings.
    for i = 1:numel(imageFiles)
        % Extract view identifiers for the current camera.
        currentFiles = imageFiles{i};
        currentViewIdentifiers = helperExtractViewIdentifiers(currentFiles);
          
        % Initialize a cell array to store aligned filenames.
        filledFiles = strings(numel(allViewIdentifiers),1);
          
        % Match views using identifiers and fill missing entries with empty strings.
        for j = 1:numel(allViewIdentifiers)
            viewID = allViewIdentifiers(j);
            matchIndex = find(currentViewIdentifiers == viewID,1);
            if ~isempty(matchIndex)
                filledFiles(j) = currentFiles(matchIndex);
            else
                % Fill missing view with an empty string.
                filledFiles(j) = "";
            end
        end
          
        % Assign the aligned and filled files to the output cell array.
        filledImageFiles{i} = filledFiles;
    end
 
    filledImageFiles = cat(2,filledImageFiles{:});

    function viewIdentifiers = helperExtractViewIdentifiers(fileNames)
        % Example of extracting view numbers from filenames.
        % Assumes filenames are in the format "view<number>.ext".
        viewIdentifiers = zeros(numel(fileNames),1);
        for k = 1:numel(fileNames)
            [~,name] = fileparts(fileNames{k});
            % Extract the numeric part of the filename.
            numStr = regexp(name,"\d+","match");
            if ~isempty(numStr)
                viewIdentifiers(k) = str2double(numStr{1});
            end
        end
    end
end

helperShowReconstructedPoints

The helperShowReconstructedPoints shows reconstructed cheetah keypoints alongside the videos.

function helperShowReconstructedPoints(xyzPoints,camPoses,videoFiles)
    
    % Create a tiled layout to display 3 videos and a 3-D plot.
    tiledlayout(2,2,TileSpacing="tight",Padding="compact");

    % Construct VideoReader objects for the footage from first 3 cameras
    % and setup their corresponding tiles.
    readers = cell(3,1);
    for i = 1:3
        readers{i} = VideoReader(videoFiles(i));
        ax = nexttile(i);
        title(ax,"Camera "+i)
    end

    % Setup the last tile to display the 3-D reconstructed points along with the cameras.
    ax = nexttile(4);

    % Plot the cameras in their respective locations.
    numCameras = length(camPoses);
    camIds = uint32(1:numCameras)';
    poses = table(camIds,camPoses,VariableNames=["ViewId","AbsolutePose"]);
    plotCamera(poses,Size=10,Parent=ax,Color="b")
    hold on
    
    % Plot the cheetah keypoints in 3 groups: tail & legs, hips & spine and head & shoulders.
    % Keypoints in group1 - tail: tip, mid, base and legs: left-back, right-back, left-front, right-front
    labelGrp1 = 1:7;
    % Keypoints in group2 - left-hip, right-hip, spine-base, spine-mid, spine-upper
    labelGrp2 = 8:12;
    % Keypoints in group3 - right-shoulder, left-shoulder, neck, left-ear, right-ear, left-eye, right-eye, nose
    labelGrp3 = 13:20;

    frameIndex = 1;
    pts1 = xyzPoints(labelGrp1,:,frameIndex);
    p1 = plot3(ax,pts1(:,1),pts1(:,2),pts1(:,3),"g*",MarkerSize=3);
    p1.XDataSource = "pts1(:,1)";
    p1.YDataSource = "pts1(:,2)";
    p1.ZDataSource = "pts1(:,3)";
    
    pts2 = xyzPoints(labelGrp2,:,frameIndex);
    p2 = plot3(ax,pts2(:,1),pts2(:,2),pts2(:,3),"c*",MarkerSize=3);
    p2.XDataSource = "pts2(:,1)";
    p2.YDataSource = "pts2(:,2)";
    p2.ZDataSource = "pts2(:,3)";
    
    pts3 = xyzPoints(labelGrp3,:,frameIndex);
    p3 = plot3(ax,pts3(:,1),pts3(:,2),pts3(:,3),"r*",MarkerSize=3);
    p3.XDataSource = "pts3(:,1)";
    p3.YDataSource = "pts3(:,2)";
    p3.ZDataSource = "pts3(:,3)";
    hold off

    xlim(ax,[-100 250]);
    ylim(ax,[-100 250]);
    zlim(ax,[-100 250]);
    legend(ax,["tail & legs","hips & spine","head & shoulders"],...
        Location="southeast")
    xlabel(ax,"X (cm)")
    ylabel(ax,"Y (cm)")
    zlabel(ax,"Z (cm)")
    title(ax,"Reconstructed Keypoints")
    view(ax,-5,-10)
    grid on

    % Display the video and the cheetah keypoints for every frame.
    numFrames = size(xyzPoints,3);
    for frameIndex = 1:numFrames
        for j = 1:3
            I = readers{j}.read(frameIndex);
            ax = nexttile(j);
            imshow(I,Parent=ax)
            title(ax,"Camera "+j)
        end
        ax = nexttile(4);
        pts1 = xyzPoints(labelGrp1,:,frameIndex); %#ok
        pts2 = xyzPoints(labelGrp2,:,frameIndex); %#ok
        pts3 = xyzPoints(labelGrp3,:,frameIndex); %#ok
    
        refreshdata(ax,"caller")
        drawnow limitrate
    end
end