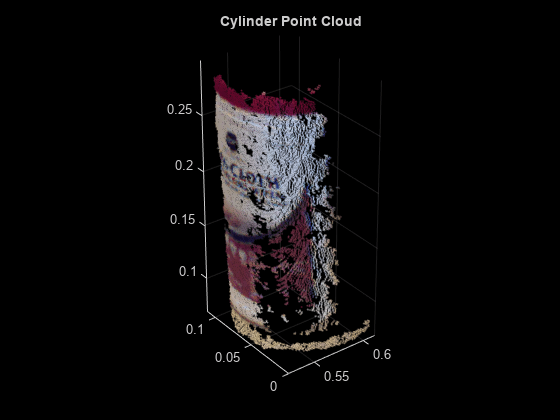
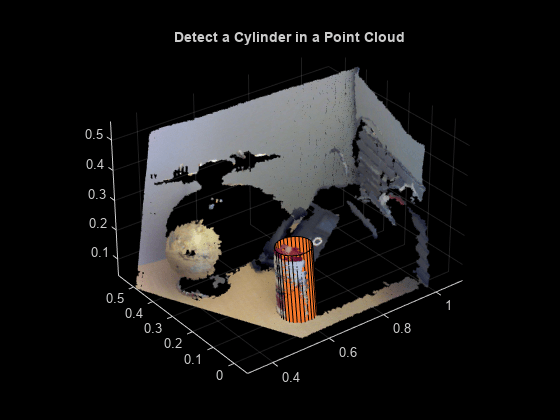
pcfitcylinder
Fit cylinder to 3-D point cloud
Syntax
Description
model = pcfitcylinder(ptCloudIn,maxDistance)
model = pcfitcylinder(ptCloudIn,maxDistance,referenceVector)
model = pcfitcylinder(ptCloudIn,maxDistance,referenceVector,maxAngularDistance)
[
additionally returns linear indices to the inlier and outlier points in the
point cloud input.model,inlierIndices,outlierIndices]
= pcfitcylinder(___)
[ additionally returns the mean error of the distance of the
inlier points to the model.model,inlierIndices,outlierIndices,meanError] =
pcfitcylinder(___)
[___] = pcfitcylinder(___,
specifies options using one or more name-value arguments in addition to any
combination of arguments from previous syntaxes. For example,
Name=Value)MaxNumTrials=1000 sets the maximum number of random
trials to 1000.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The function returns a geometric model that describes the cylinder. This function uses the M-estimator SAmple Consensus (MSAC) algorithm to find the cylinder. The MSAC algorithm is a variant of the RANdom SAmple Consensus (RANSAC) algorithm.
The fitting algorithm for the pcfitcylinder function
requires point cloud normals. Therefore, if the Normal property
for the input point cloud is empty, the function fills it. When the
function fills the Normal property, it uses six points
to fit the local cylinder. If six points do not work and the fitting
fails, consider calling the pcnormals function
which enables you to select the number of points to use.
References
[1] Torr, P. H. S., and A. Zisserman. “MLESAC: A New Robust Estimator with Application to Estimating Image Geometry.” Computer Vision and Image Understanding. Volume 78, Issue 1, April 2000, pp. 138-156.
Extended Capabilities
Version History
Introduced in R2015b
See Also
Objects
Functions
pcfitplane|pcfitsphere|findPointsInROI|pcplayer|pcshow|pcwrite|pcread|pcmerge|pctransform|pcregistericp|pcdenoise