barometerSensor

Barometer sensor model with noise

Since R2025a

Description

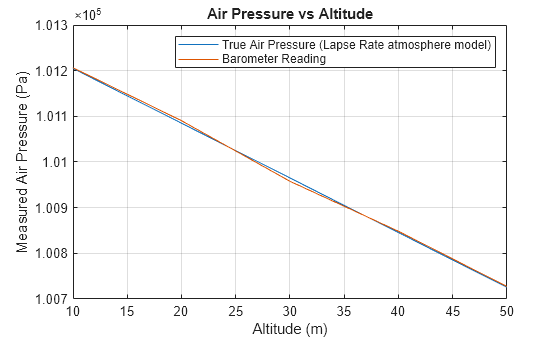
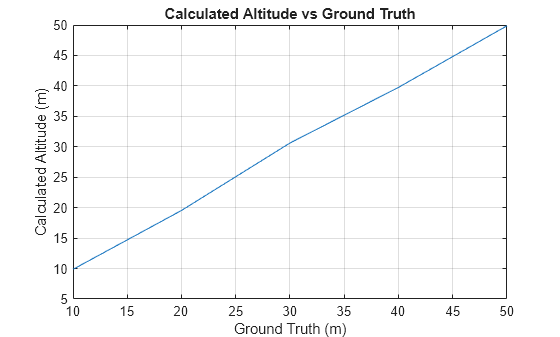
The barometerSensor System object™ models a barometer sensor that generates an air pressure reading with a measurement noise that consists of constant measurement bias, uncorrelated white noise, and correlated noise [1]. For more information on the noise model, see Noise Model.

To simulate a barometer sensor:

1. Create the barometerSensor object and set its properties.

2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

barometer = barometerSensor

barometer = barometerSensor(PropertyName=Value)

Description

barometer = barometerSensor returns a barometerSensor System object that simulates barometer readings.

barometer = barometerSensor(PropertyName=Value) returns a barometerSensor System object with each property name set to the specified value.

Properties

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

SampleRate — Sensor sample rate

10 (default) | positive scalar

Sensor sample rate in Hz, specified as a positive scalar.

Data Types: single | double

ConstantBias — Constant measurement bias

0 (default) | finite scalar

Constant measurement bias in Pa, specified as a finite scalar.

Tunable: Yes

Data Types: single | double

NoiseDensity — White noise standard variance

1 (default) | nonnegative finite scalar

White noise standard variance, specified as a nonnegative finite scalar. This property specifies the power spectral density of the sensor noise in Pa/√Hz.

Tunable: Yes

Data Types: single | double

BiasInstability — Correlated noise standard variance

1 (default) | nonnegative finite scalar

Correlated noise standard variance in Pa, specified as a nonnegative finite scalar.

Tunable: Yes

Data Types: single | double

DecayFactor — Correlated noise decay factor

0.99 (default) | scalar in range (0, 1)

Correlated noise decay factor, specified as a scalar in the range (0, 1).

Specifying a smaller decay factor models the correlated noise closer to white noise, while specifying a larger decay factor models the correlated noise closer to a random walk process.

Tunable: Yes

Data Types: single | double

RandomStream — Random number source

"Global stream" (default) | "mt19937ar with seed"

Random number source, specified as one of these values:

• "Global stream" — Generate random numbers using the current global random number stream.

• "mt19937ar with seed" — Generate random numbers using the mt19937ar algorithm with the seed specified by the RandomSeed property.

Data Types: char | string

RandomSeed — Random number initial seed

67 (default) | real nonnegative integer

Random number initial seed, specified as a real nonnegative integer. This property specifies the initial seed of the mt19937ar algorithm.

Dependencies

To enable this property, set RandomStream property to "mt19937ar with seed".

Data Types: single | double

Usage

Syntax

barometerReading = barometer(airPressure)

Description

barometerReading = barometer(airPressure) generates a measured air pressure reading from a true air pressure input.

Input Arguments

airPressure — True air pressure

scalar | N-element vector

True air pressure in Pa, specified as a scalar or N-element vector, where N is the number of air pressure measurements.

Data Types: single | double

Output Arguments

barometerReading — Measured air pressure

nonnegative scalar | N-element vector

Measured air pressure in Pa, returned as a nonnegative scalar or N-element vector. The length of barometerReading matches the length of airPressure

Data Types: single | double

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

Common to All System Objects

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

Generate Air Pressure Reading from Altitude

Specify a selection of altitudes in meters.

altitude = [10 20 30 40 50];

Use the atmoslapse (Aerospace Toolbox) atmospheric model to obtain the true air pressure at the specified altitudes.

g = 9.81;                   % Gravity acceleration in m/s^2
gamma = 1.4;                % Heat ratio
R = 287.0531;               % Characteristic gas constant in J/(kg*K)
L = 0.0065;                 % Lapse rate in K/m
heightTroposphere = 10000;  % Height of troposphere in m
heightTropopause = 20000;   % Height of tropopause in m
rho0 = 1.225;               % Air density at sea level in kg/m^3
T0 = 288.15;                % Temperature at sea level in K
P0 = 101325;                % Atmospheric Pressure at sea level in Pa

[~,~,pTrue] = atmoslapse(altitude,g,gamma,R,L, ...
    heightTroposphere,heightTropopause,rho0,P0,T0);

Create a barometer sensor with default parameters.

barometer = barometerSensor;

Obtain the air pressure reading from the true air pressure.

pMeasured = barometer(pTrue);

Plot the true air pressure and measured air pressure with respect to altitude.

plot(altitude,pTrue)
hold on
plot(altitude,pMeasured)
title("Air Pressure vs Altitude")
xlabel("Altitude (m)")
ylabel("Measured Air Pressure (Pa)")
legend(["True Air Pressure (Lapse Rate atmosphere model)","Barometer Reading"])
grid on
hold off

Use atmospalt (Aerospace Toolbox) to calculate the altitude above mean sea level in meters by using the measured air pressure.

pressureAltitude = atmospalt(pMeasured);

Plot the calculated altitude againts ground truth altitude.

plot(altitude,pressureAltitude);
title("Calculated Altitude vs Ground Truth")
xlabel("Ground Truth (m)")
ylabel("Calculated Altitude (m)")
grid on

Identify Barometer Noise Parameters from PX4 Flight Log

Identifying barometer noise parameters from a PX4 flight log enables you to create a barometer object with a similar noise characteristic to the barometer sensor that your flight controller uses.

Extract Barometer Data from Flight Log

Read the sample PX4 flight log.

logFile = "sampleLogBarometerExample.ulg";
data = ulogreader(logFile);

Read the vehicle_air_data topic.

airdataTopic = readTopicMsgs(data,TopicNames="vehicle_air_data");
airdataTopicMessages = airdataTopic.TopicMessages{1};

Extract the baro_pressure_pa message as a timetable that contains the measured air pressure in pascals.

timePeriodStart = airdataTopicMessages.timestamp(1);
timePeriodEnd = airdataTopicMessages.timestamp(end);
baroPressurePa = airdataTopicMessages(airdataTopicMessages.timestamp < timePeriodEnd ...
    & airdataTopicMessages.timestamp > timePeriodStart,"baro_pressure_pa");

Preprocess the measured air pressure data by resampling it to a fixed interval of 0.5 seconds, and by removing the absolute air pressure to isolate the noise component.

barometerTs = 0.05;
baroPressurePa = retime(baroPressurePa,timePeriodStart:seconds(barometerTs):timePeriodEnd,"linear");
baroPressurePaNoise = baroPressurePa.baro_pressure_pa - mean(baroPressurePa.baro_pressure_pa(1:1000));

Identify Noise Parameters with ARMA Model

To identify the noise parameters, model the barometer noise with autoregressive moving average (ARMA) model, given by the equation:

.

Create an iddata object to store the time-domain output of the air pressure measurement, and then use the armax function to estimate the parameters of the ARMA model.

baroPressurePaNoiseDouble = double(baroPressurePaNoise);
sysdata = iddata(baroPressurePaNoiseDouble,[],barometerTs);
[sys,ic] = armax(sysdata,[1 1]);

The overall barometer noise shaping filter is given by

.

By comparing the terms of the ARMA model and the barometer noise shaping filter, you can determine that:

In addition, is the standard deviation of the ARMA system noise.

a = sys.A(2);
b = sys.C(2);
Ho = sqrt(sys.NoiseVariance);

Obtain the barometer sensor decay factor.

barometerDecayFactor = -a;

Obtain the barometer sensor noise density.

tauO = (1-b)/(1+b)*barometerTs/2;
tauP = (1-a)/(1+a)*barometerTs/2;
tau = tauP;
sqrtOfSumOfSquares = Ho*(1+2*tauP/barometerTs)/(1+2*tauO/barometerTs);
alpha = tauO/tau*sqrtOfSumOfSquares;
sigmaU = alpha;
barometerNoiseDensity = sigmaU/sqrt(barometerTs);

Obtain the barometer sensor bias instability.

beta = sqrtOfSumOfSquares*sqrt(1-(tauO/tau)^2);
barometerBiasInstability = beta/sqrt(2*tau);

Create a barometer sensor object with the parameters that you obtained.

barometerModel = barometerSensor(SampleRate=barometerTs,NoiseDensity=barometerNoiseDensity, ...
    BiasInstability=barometerBiasInstability,DecayFactor=barometerDecayFactor)

barometerModel = 
  barometerSensor with properties:

         SampleRate: 0.05               Hz    
       ConstantBias: 0                  Pa    
       NoiseDensity: 7.242              Pa/√Hz
    BiasInstability: 247.2              Pa    
        DecayFactor: 1                        
       RandomStream: 'Global stream'          

Algorithms

Noise Model

This equation represents the measurement noise that is added to the true air pressure:

$$n(t)=n_c(t)+n_u(t)+b.$$

b is the constant measurement bias that you set by using the ConstantBias property. n_u(t) is the uncorrelated noise that is modeled as white Gaussian noise with zero mean and variance that you set by using the NoiseDensity property. n_c(t) is the correlated noise given by this equation:

$$n_c\left(N+1\right)=D{n}_c\left(N\right)+\left(1-D\right)\sqrt{\frac{-2}{\log \left(D\right)}}Bw,$$

where:

• n_c(N) is the correlated noise at the N^th time step.

• w is the white Gaussian noise with unit variance.

• D is the decay factor that you set by using the DecayFactor property.

• B is the bias instability that you set by using the BiasInstability property.

References

[1] Sabatini, Angelo, and Vincenzo Genovese. “A Stochastic Approach to Noise Modeling for Barometric Altimeters.” Sensors 13, no. 11 (November 18, 2013): 15692–707. https://doi.org/10.3390/s131115692.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2025a