ldaModel

Latent Dirichlet allocation (LDA) model

Description

A latent Dirichlet allocation (LDA) model is a topic model which discovers underlying topics in a collection of documents and infers word probabilities in topics. If the model was fit using a bag-of-n-grams model, then the software treats the n-grams as individual words.

Creation

Create an LDA model using the fitlda function.

Properties

NumTopics — Number of topics

positive integer

Number of topics in the LDA model, specified as a positive integer.

TopicConcentration — Topic concentration

positive scalar

Topic concentration, specified as a positive scalar. The function sets the concentration per topic to TopicConcentration/NumTopics. For more information, see Latent Dirichlet Allocation.

WordConcentration — Word concentration

1 (default) | nonnegative scalar

Word concentration, specified as a nonnegative scalar. The software sets the concentration per word to WordConcentration/numWords, where numWords is the vocabulary size of the input documents. For more information, see Latent Dirichlet Allocation.

CorpusTopicProbabilities — Topic probabilities of input document set

vector

Topic probabilities of input document set, specified as a vector. The corpus topic probabilities of an LDA model are the probabilities of observing each topic in the entire data set used to fit the LDA model. CorpusTopicProbabilities is a 1-by-K vector where K is the number of topics. The kth entry of CorpusTopicProbabilities corresponds to the probability of observing topic k.

DocumentTopicProbabilities — Topic probabilities per input document

matrix

Topic probabilities per input document, specified as a matrix. The document topic probabilities of an LDA model are the probabilities of observing each topic in each document used to fit the LDA model. DocumentTopicProbabilities is a D-by-K matrix where D is the number of documents used to fit the LDA model, and K is the number of topics. The (d,k)th entry of DocumentTopicProbabilities corresponds to the probability of observing topic k in document d.

If any the topics have zero probability (CorpusTopicProbabilities contains zeros), then the corresponding columns of DocumentTopicProbabilities and TopicWordProbabilities are zeros.

The order of the rows in DocumentTopicProbabilities corresponds to the order of the documents in the training data.

TopicWordProbabilities — Word probabilities per topic

matrix

Word probabilities per topic, specified as a matrix. The topic word probabilities of an LDA model are the probabilities of observing each word in each topic of the LDA model. TopicWordProbabilities is a V-by-K matrix, where V is the number of words in Vocabulary and K is the number of topics. The (v,k)th entry of TopicWordProbabilities corresponds to the probability of observing word v in topic k.

If any the topics have zero probability (CorpusTopicProbabilities contains zeros), then the corresponding columns of DocumentTopicProbabilities and TopicWordProbabilities are zeros.

The order of the rows in TopicWordProbabilities corresponds to the order of the words in Vocabulary.

TopicOrder — Topic order

'initial-fit-probability' (default) | 'unordered'

Topic order, specified as one of the following:

• 'initial-fit-probability' – Sort the topics by the corpus topic probabilities of the initial model fit. These probabilities are the CorpusTopicProbabilities property of the initial ldaModel object returned by fitlda. The resume function does not reorder the topics of the resulting ldaModel objects.

• 'unordered' – Do not order topics.

FitInfo — Information recorded when fitting LDA model

struct

Information recorded when fitting LDA model, specified as a struct with the following fields:

• TerminationCode – Status of optimization upon exit

  • 0 – Iteration limit reached.

  • 1 – Tolerance on log-likelihood satisfied.

• TerminationStatus – Explanation of the returned termination code

• NumIterations – Number of iterations performed

• NegativeLogLikelihood – Negative log-likelihood for the data passed to fitlda

• Perplexity – Perplexity for the data passed to fitlda

• Solver – Name of the solver used

• History – Struct holding the optimization history

• StochasticInfo – Struct holding information for stochastic solvers

Data Types: struct

Vocabulary — List of words in the model

string vector

List of words in the model, specified as a string vector.

Data Types: string

Object Functions

logp	Document log-probabilities and goodness of fit of LDA model
predict	Predict top LDA topics of documents
resume	Resume fitting LDA model
topkwords	Most important words in bag-of-words model or LDA topic
transform	Transform documents into lower-dimensional space
wordcloud	Create word cloud chart from text, bag-of-words model, bag-of-n-grams model, or LDA model

Examples

Fit LDA Model

To reproduce the results in this example, set rng to 'default'.

rng('default')

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Create a bag-of-words model using bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154×3092 double]
      Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    "contracted"    …    ]
        NumWords: 3092
    NumDocuments: 154

Fit an LDA model with four topics.

numTopics = 4;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.263378 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.17 |            |  1.215e+03 |         1.000 |             0 |
|          1 |       0.02 | 1.0482e-02 |  1.128e+03 |         1.000 |             0 |
|          2 |       0.02 | 1.7190e-03 |  1.115e+03 |         1.000 |             0 |
|          3 |       0.01 | 4.3796e-04 |  1.118e+03 |         1.000 |             0 |
|          4 |       0.01 | 9.4193e-04 |  1.111e+03 |         1.000 |             0 |
|          5 |       0.01 | 3.7079e-04 |  1.108e+03 |         1.000 |             0 |
|          6 |       0.01 | 9.5777e-05 |  1.107e+03 |         1.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 4
             WordConcentration: 1
            TopicConcentration: 1
      CorpusTopicProbabilities: [0.2500 0.2500 0.2500 0.2500]
    DocumentTopicProbabilities: [154×4 double]
        TopicWordProbabilities: [3092×4 double]
                    Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    …    ]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1×1 struct]

Visualize the topics using word clouds.

figure
for topicIdx = 1:4
    subplot(2,2,topicIdx)
    wordcloud(mdl,topicIdx);
    title("Topic: " + topicIdx)
end

Highest Probability Words of LDA Topic

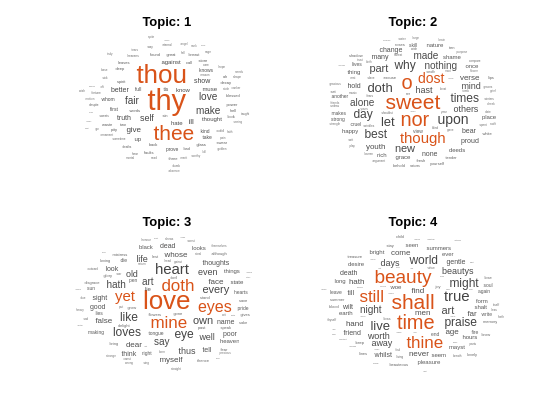
Create a table of the words with highest probability of an LDA topic.

To reproduce the results, set rng to 'default'.

rng('default')

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Create a bag-of-words model using bagOfWords.

bag = bagOfWords(documents);

Fit an LDA model with 20 topics. To suppress verbose output, set 'Verbose' to 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0);

Find the top 20 words of the first topic.

k = 20;
topicIdx = 1;
tbl = topkwords(mdl,k,topicIdx)

tbl=20×2 table
      Word        Score  
    ________    _________

    "eyes"        0.11155
    "beauty"      0.05777
    "hath"       0.055778
    "still"      0.049801
    "true"       0.043825
    "mine"       0.033865
    "find"       0.031873
    "black"      0.025897
    "look"       0.023905
    "tis"        0.023905
    "kind"       0.021913
    "seen"       0.021913
    "found"      0.017929
    "sin"        0.015937
    "three"      0.013945
    "golden"    0.0099608
      ⋮

Find the top 20 words of the first topic and use inverse mean scaling on the scores.

tbl = topkwords(mdl,k,topicIdx,'Scaling','inversemean')

tbl=20×2 table
      Word       Score  
    ________    ________

    "eyes"        1.2718
    "beauty"     0.59022
    "hath"        0.5692
    "still"      0.50269
    "true"       0.43719
    "mine"       0.32764
    "find"       0.32544
    "black"      0.25931
    "tis"        0.23755
    "look"       0.22519
    "kind"       0.21594
    "seen"       0.21594
    "found"      0.17326
    "sin"        0.15223
    "three"      0.13143
    "golden"    0.090698
      ⋮

Create a word cloud using the scaled scores as the size data.

figure
wordcloud(tbl.Word,tbl.Score);

Document Topic Probabilities of LDA Model

Get the document topic probabilities (also known as topic mixtures) of the documents used to fit an LDA model.

To reproduce the results, set rng to 'default'.

rng('default')

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Create a bag-of-words model using bagOfWords.

bag = bagOfWords(documents);

Fit an LDA model with 20 topics. To suppress verbose output, set 'Verbose' to 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0)

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    ...    ] (1x3092 string)
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

View the topic probabilities of the first document in the training data.

topicMixtures = mdl.DocumentTopicProbabilities;
figure
bar(topicMixtures(1,:))
title("Document 1 Topic Probabilities")
xlabel("Topic Index")
ylabel("Probability")

Predict Top LDA Topics of Documents

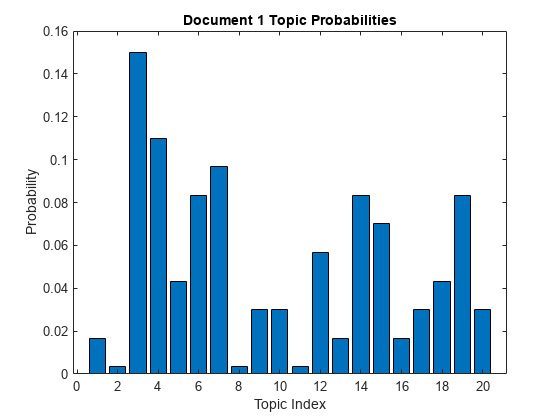
To reproduce the results in this example, set rng to 'default'.

rng('default')

Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Create a bag-of-words model using bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154×3092 double]
      Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    "contracted"    …    ]
        NumWords: 3092
    NumDocuments: 154

Fit an LDA model with 20 topics.

numTopics = 20;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.513255 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.04 |            |  1.159e+03 |         5.000 |             0 |
|          1 |       0.05 | 5.4884e-02 |  8.028e+02 |         5.000 |             0 |
|          2 |       0.04 | 4.7400e-03 |  7.778e+02 |         5.000 |             0 |
|          3 |       0.04 | 3.4597e-03 |  7.602e+02 |         5.000 |             0 |
|          4 |       0.03 | 3.4662e-03 |  7.430e+02 |         5.000 |             0 |
|          5 |       0.03 | 2.9259e-03 |  7.288e+02 |         5.000 |             0 |
|          6 |       0.03 | 6.4180e-05 |  7.291e+02 |         5.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500]
    DocumentTopicProbabilities: [154×20 double]
        TopicWordProbabilities: [3092×20 double]
                    Vocabulary: ["fairest"    "creatures"    "desire"    "increase"    "thereby"    "beautys"    "rose"    "might"    "never"    "die"    "riper"    "time"    "decease"    "tender"    "heir"    "bear"    "memory"    "thou"    …    ]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1×1 struct]

Predict the top topics for an array of new documents.

newDocuments = tokenizedDocument([
    "what's in a name? a rose by any other name would smell as sweet."
    "if music be the food of love, play on."]);
topicIdx = predict(mdl,newDocuments)

topicIdx = 2×1

    19
     8

Visualize the predicted topics using word clouds.

figure
subplot(1,2,1)
wordcloud(mdl,topicIdx(1));
title("Topic " + topicIdx(1))
subplot(1,2,2)
wordcloud(mdl,topicIdx(2));
title("Topic " + topicIdx(2))

More About

Latent Dirichlet Allocation

A latent Dirichlet allocation (LDA) model is a document topic model which discovers underlying topics in a collection of documents and infers word probabilities in topics. LDA models a collection of D documents as topic mixtures $${\theta }_1,\dots ,{\theta }_D$$, over K topics characterized by vectors of word probabilities $${\phi }_1,\dots ,{\phi }_K$$. The model assumes that the topic mixtures $${\theta }_1,\dots ,{\theta }_D$$, and the topics $${\phi }_1,\dots ,{\phi }_K$$ follow a Dirichlet distribution with concentration parameters $$\alpha$$ and $$\beta$$ respectively.

The topic mixtures $${\theta }_1,\dots ,{\theta }_D$$ are probability vectors of length K, where K is the number of topics. The entry $${\theta }_{di}$$ is the probability of topic i appearing in the dth document. The topic mixtures correspond to the rows of the DocumentTopicProbabilities property of the ldaModel object.

The topics $${\phi }_1,\dots ,{\phi }_K$$ are probability vectors of length V, where V is the number of words in the vocabulary. The entry $${\phi }_{iv}$$ corresponds to the probability of the vth word of the vocabulary appearing in the ith topic. The topics $${\phi }_1,\dots ,{\phi }_K$$ correspond to the columns of the TopicWordProbabilities property of the ldaModel object.

Given the topics $${\phi }_1,\dots ,{\phi }_K$$ and Dirichlet prior $$\alpha$$ on the topic mixtures, LDA assumes the following generative process for a document:

1. Sample a topic mixture $$\theta ~\text{Dirichlet}(\alpha )$$. The random variable $$\theta$$ is a probability vector of length K, where K is the number of topics.

2. For each word in the document:

   1. Sample a topic index $$z~\text{Categorical}(\theta )$$. The random variable z is an integer from 1 through K, where K is the number of topics.

   2. Sample a word $$w~\text{Categorical}({\phi }_z)$$. The random variable w is an integer from 1 through V, where V is the number of words in the vocabulary, and represents the corresponding word in the vocabulary.

Under this generative process, the joint distribution of a document with words $$w_1,\dots ,w_N$$, with topic mixture $$\theta$$, and with topic indices $$z_1,\dots ,z_N$$ is given by

$$p(\theta ,z,w|\alpha ,\phi )=p(\theta |\alpha ){\displaystyle \prod _{n=1}^{N}p}(z_n|\theta )p(w_n|z_n,\phi ),$$

where N is the number of words in the document. Summing the joint distribution over z and then integrating over $$\theta$$ yields the marginal distribution of a document w:

$$p(w|\alpha ,\phi )={\displaystyle \underset{\theta }{\int }p(\theta |\alpha ){\displaystyle \prod _{n=1}^N{\displaystyle \sum _{z_n}p(z_n|\theta )p(w_n|z_n,\phi )}}}d\theta .$$

The following diagram illustrates the LDA model as a probabilistic graphical model. Shaded nodes are observed variables, unshaded nodes are latent variables, nodes without outlines are the model parameters. The arrows highlight dependencies between random variables and the plates indicate repeated nodes.

Dirichlet Distribution

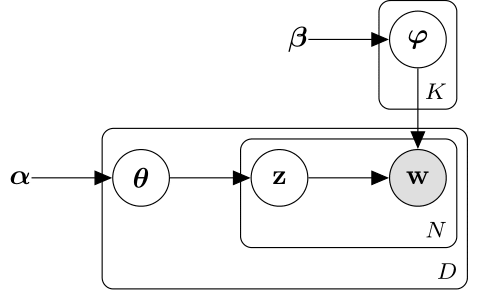
The Dirichlet distribution is a continuous generalization of the multinomial distribution. Given the number of categories $$K\ge 2$$, and concentration parameter $$\alpha$$, where $$\alpha$$ is a vector of positive reals of length K, the probability density function of the Dirichlet distribution is given by

$$p(\theta \mid \alpha )=\frac{1}{B(\alpha )}{\displaystyle \prod }_{i=1}^K\text{}{\theta }_i^{{\alpha }_i-1},$$

where B denotes the multivariate Beta function given by

$$B(\alpha )=\frac{{\displaystyle \prod }_{i=1}^K\text{}\Gamma \text{}\text{(}{\alpha }_i)}{\Gamma \left({\displaystyle \sum }_{i=1}^K\text{}{\alpha }_i\right)}.$$

A special case of the Dirichlet distribution is the symmetric Dirichlet distribution. The symmetric Dirichlet distribution is characterized by the concentration parameter $$\alpha$$, where all the elements of $$\alpha$$ are the same.

Version History

Introduced in R2017b