The Black–Scholes Formula for Call Option Price

Find Call Option Price

The Black–Scholes formula models the price of European call options [1]. For a non-dividend-paying underlying stock, the parameters of the formula are defined as:

The price of a call option $$C$$ in terms of the Black–Scholes parameters is

$$C=N(d_1)\times S-N(d_2)\times PV(K)$$,

where:

Find the price of a European stock option that expires in three months with an exercise price of $95. Assume that the underlying stock pays no dividend, trades at $100, and has a volatility of 50% per annum. The risk-free rate is 1% per annum.

Use sym to create symbolic numbers that represent the values of the Black–Scholes parameters.

syms t d
S = sym(100);        % current stock price (spot price)
K = sym(95);         % exercise price (strike price)
sigma = sym(0.50);   % volatility of stock
T = sym(3/12);       % expiry time in years
r = sym(0.01);       % annualized risk-free interest rate

Calculate the option price without approximation. Create a symbolic function N(d) that represents the standard normal cumulative distribution function.

PV_K = K*exp(-r*T);
d1 = (log(S/K) + (r + sigma^2/2)*T)/(sigma*sqrt(T));
d2 = d1 - sigma*sqrt(T);
N(d) = int(exp(-((t)^2)/2),t,-Inf,d)*1/sqrt(2*sym(pi))

N(d) = 
$$\frac{\mathrm{erf}\left(\frac{\sqrt{2}\hspace{0.17em}d}{2}\right)}{2}+\frac{1}{2}$$

Csym = N(d1)*S - N(d2)*PV_K

Csym = 
$$50\hspace{0.17em}\mathrm{erf}\left(\frac{\sqrt{2}\hspace{0.17em}\left(4\hspace{0.17em}\log \left(\frac{20}{19}\right)+\frac{27}{200}\right)}{2}\right)-95\hspace{0.17em}{\mathrm{e}}^{-\frac{1}{400}}\hspace{0.17em}\left(\frac{\mathrm{erf}\left(\frac{\sqrt{2}\hspace{0.17em}\left(4\hspace{0.17em}\log \left(\frac{20}{19}\right)-\frac{23}{200}\right)}{2}\right)}{2}+\frac{1}{2}\right)+50$$

To obtain the numeric result with variable precision, use vpa. By default, vpa returns a number with 32 significant digits.

Cvpa = vpa(Csym)

Cvpa = $$12.52792339252145394554497137187$$

To change the precision, use digits. The price of the option to 6 significant digits is $12.5279.

digits(6)
Cvpa = vpa(Csym)

Cvpa = $$12.5279$$

Plot Call Option Price

Next, suppose that for the same stock option the time to expiry changes and the day-to-day stock price is unknown. Find the price of this call option for expiry time $$T$$ that varies from 0 to 0.25 years, and spot price $$S$$ that varies from $50 to $140. Use the values for exercise rate (K), volatility (sigma), and interest rate (r) from the previous example. In this case, use the time to expiry T and day-to-day stock price S as the variable quantities.

Define the symbolic expression C to represent the call option price with T and S as the unknown variables.

syms T S

PV_K = K*exp(-r*T);
d1 = (log(S/K) + (r + sigma^2/2)*T)/(sigma*sqrt(T));
d2 = d1 - sigma*sqrt(T);
Nd1 = int(exp(-((t)^2)/2),-Inf,d1)*1/sqrt(2*pi);
Nd2 = int(exp(-((t)^2)/2),-Inf,d2)*1/sqrt(2*pi);
C = Nd1*S - Nd2*PV_K;

Plot the call option price as a function of spot price and expiry time.

fsurf(C,[50 140 0 0.25])
xlabel('Spot price')
ylabel('Expiry time')
zlabel('Call option price')

Calculate the call option price with expiry time 0.1 years and spot price $105. Use subs to substitute the values of T and S to the expression C. Return the price as a numeric result using vpa.

Csym = subs(C,[T S],[0.1 105]);
Cvpa = vpa(Csym)

Cvpa = $$12.5868$$

Find Spot Price

Consider the case where the option price is changing, and you want to know how this affects the underlying stock price. This is a problem of finding $$S$$ from the Black–Scholes formula given the known parameters $$K$$, $$\sigma$$, $$T$$, $$r$$, and $$C$$.

For example, after one month, the price of the same call option now trades at $15.04 with expiry time of two months. Find the spot price of the underlying stock. Create a symbolic function C(S) that represents the Black–Scholes formula with the unknown parameter S.

syms C(S) d1(S) d2(S) Nd1(S) Nd2(S)

K = 95;         % exercise price (strike price)
sigma = 0.50;   % volatility of stock
T = 2/12;       % expiry time in years
r = 0.01;       % annualized risk-free interest rate

PV_K = K*exp(-r*T);
d1(S) = (log(S/K) + (r + sigma^2/2)*T)/(sigma*sqrt(T));
d2(S) = d1 - sigma*sqrt(T);
Nd1(S) = int(exp(-((t)^2)/2),-Inf,d1)*1/sqrt(2*pi);
Nd2(S) = int(exp(-((t)^2)/2),-Inf,d2)*1/sqrt(2*pi);
C(S) = Nd1*S - Nd2*PV_K;

Use vpasolve to numerically solve for the spot price of the underlying stock. Search for solutions only in the positive numbers. The spot price of the underlying stock is $106.162.

S_Sol = vpasolve(C(S) == 15.04,S,[0 Inf])

S_Sol = $$106.162$$

Find Implied Volatility

Consider the case where the option price is changing and you want to know what is the implied volatility. This is a problem of finding the value of $$\sigma$$ from the Black–Scholes formula given the known parameters $$S$$, $$K$$, $$T$$, $$r$$, and $$C$$.

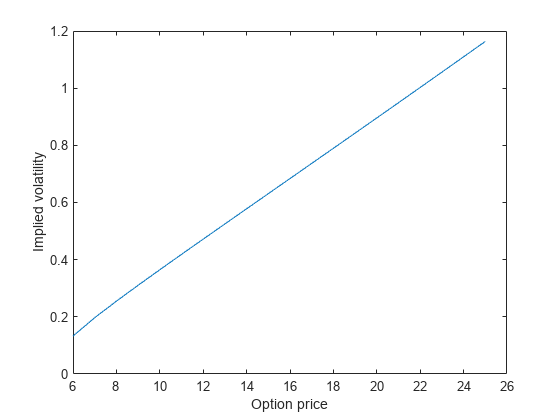
Consider the same stock option that expires in three months with an exercise price of $95. Assume that the underlying stock trades at $100, and the risk-free rate is 1% per annum. Find the implied volatility as a function of option price that ranges from $6 to $25. Create a vector for the range of the option price. Create a symbolic function C(sigma) that represents the Black–Scholes formula with the unknown parameter sigma. Use vpasolve to numerically solve for the implied volatility.

syms C(sigma) d1(sigma) d2(sigma) Nd1(sigma) Nd2(sigma)

S = 100;        % current stock price (spot price)
K = 95;         % exercise price (strike price)
T = 3/12;       % expiry time in years
r = 0.01;       % annualized risk-free interest rate
C_Range = 6:25; % range of option price
sigma_Sol = zeros(size(C_Range));

PV_K = K*exp(-r*T);
d1(sigma) = (log(S/K) + (r + sigma^2/2)*T)/(sigma*sqrt(T));
d2(sigma) = d1 - sigma*sqrt(T);
Nd1(sigma) = int(exp(-((t)^2)/2),-Inf,d1)*1/sqrt(2*pi);
Nd2(sigma) = int(exp(-((t)^2)/2),-Inf,d2)*1/sqrt(2*pi);
C(sigma) = Nd1*S - Nd2*PV_K;
for i = 1:length(C_Range)
    sigma_Sol(i) = vpasolve(C(sigma) == C_Range(i),sigma,[0 Inf]);
end

Plot the implied volatility as a function of the option price.

plot(C_Range,sigma_Sol)
xlabel('Option price')
ylabel('Implied volatility')

Reference

[1] https://en.wikipedia.org/wiki/Black–Scholes_model