Solve a system of two second-order PDEs. You can solve the PDE system by extracting the PDE coefficients symbolically using pdeCoefficients, converting the coefficients to double-precision numbers using pdeCoefficientsToDouble, and specifying the coefficients in the PDE model using specifyCoefficients.
The system of PDEs represents the deflection of a clamped structural plate under a uniform pressure load. The system of PDEs with the dependent variables and is given by
,
,
where is the bending stiffness of the plate given by
,
and is the modulus of elasticity, is Poisson's ratio, is the plate thickness, is the transverse deflection of the plate, and is the pressure load.
Create a PDE model for the system of two equations.
Create a square geometry. Specify the side length of the square. Then include the geometry in the PDE model.
Specify the values of the physical parameters of the system. Let the external pressure be a symbolic variable pres that can take any value.
Declare the PDE system as a system symbolic equations. Extract the coefficients of the PDE and return them in symbolic form.
symCoeffs = struct with fields:
m: 0
a: [2×2 sym]
c: [4×4 sym]
f: [2×1 sym]
d: 0
Display the coefficients m, a, c, f, and d.
Substitute a value for pres using the subs function. Since the outputs of subs are symbolic objects, use the pdeCoefficientsToDouble function to convert the coefficients to the double data type, which makes them valid inputs for the Partial Differential Equation Toolbox.
coeffs = struct with fields:
a: [4×1 double]
c: [16×1 double]
m: 0
d: 0
f: [2×1 double]
Specify the PDE coefficients for the PDE model.
Specify spring stiffness. Specify boundary conditions by defining distributed springs on all four edges.
Specify the mesh size of the geometry and generate a mesh for the PDE model.
Solve the model.
Access the solution at the nodal locations.
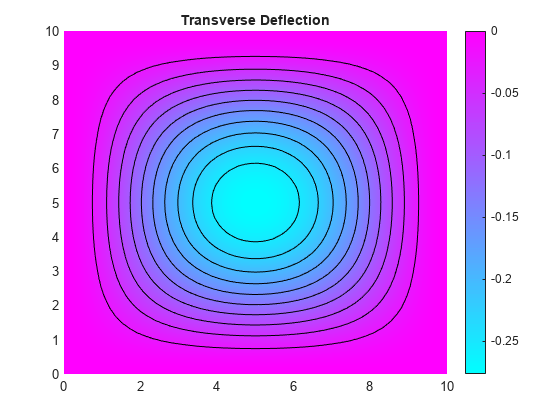
Plot the transverse deflection of the plate.
Find the transverse deflection at the plate center.
Compare the result with the deflection at the plate center computed analytically.