pade
Pade approximant
Description
pade( returns
the third-order Padé approximant of the expression f,var)f at var
= 0. For details, see Padé Approximant.
If you do not specify var, then pade uses
the default variable determined by symvar(f,1).
pade(___, uses
additional options specified by one or more Name,Value)Name,Value pair
arguments. You can specify Name,Value after the
input arguments in any of the previous syntaxes.
Examples
Find Padé Approximant for Symbolic Expressions
Find the Padé approximant of sin(x).
By default, pade returns a third-order Padé
approximant.
syms x pade(sin(x))
ans = -(x*(7*x^2 - 60))/(3*(x^2 + 20))
Specify Expansion Variable
If you do not specify the expansion variable, symvar selects
it. Find the Padé approximant of sin(x) + cos(y).
The symvar function chooses x as
the expansion variable.
syms x y pade(sin(x) + cos(y))
ans = (- 7*x^3 + 3*cos(y)*x^2 + 60*x + 60*cos(y))/(3*(x^2 + 20))
Specify the expansion variable as y. The pade function
returns the Padé approximant with respect to y.
pade(sin(x) + cos(y),y)
ans = (12*sin(x) + y^2*sin(x) - 5*y^2 + 12)/(y^2 + 12)
Approximate Value of Function at Particular Point
Find the value of tan(3*pi/4).
Use pade to find the Padé approximant for tan(x) and
substitute into it using subs to find tan(3*pi/4).
syms x f = tan(x); P = pade(f); y = subs(P,x,3*pi/4)
y = (pi*((9*pi^2)/16 - 15))/(4*((9*pi^2)/8 - 5))
Use vpa to convert y into
a numeric value.
vpa(y)
ans = -1.2158518789569086447244881326842
Increase Accuracy of Padé Approximant
You can increase the accuracy of the Padé
approximant by increasing the order. If the expansion point is a pole
or a zero, the accuracy can also be increased by setting OrderMode to relative.
The OrderMode option has no effect if the expansion
point is not a pole or zero.
Find the Padé approximant of tan(x) using pade with
an expansion point of 0 and Order of [1
1]. Find the value of tan(1/5) by substituting
into the Padé approximant using subs, and
use vpa to convert 1/5 into
a numeric value.
syms x p11 = pade(tan(x),x,0,'Order',[1 1]) p11 = subs(p11,x,vpa(1/5))
p11 = x p11 = 0.2
Find the approximation error by subtracting p11 from
the actual value of tan(1/5).
y = tan(vpa(1/5)); error = y - p11
error = 0.0027100355086724833213582716475345
Increase the accuracy of the Padé approximant by increasing
the order using Order. Set Order to [2
2], and find the error.
p22 = pade(tan(x),x,0,'Order',[2 2]) p22 = subs(p22,x,vpa(1/5)); error = y - p22
p22 = -(3*x)/(x^2 - 3) error = 0.0000073328059697806186555689448317799
The accuracy increases with increasing order.
If the expansion point is a pole or zero, the accuracy of the
Padé approximant decreases. Setting the OrderMode option
to relative compensates for the decreased accuracy.
For details, see Padé Approximant.
Because the tan function has a zero at 0,
setting OrderMode to relative increases
accuracy. This option has no effect if the expansion point is not
a pole or zero.
p22Rel = pade(tan(x),x,0,'Order',[2 2],'OrderMode','relative') p22Rel = subs(p22Rel,x,vpa(1/5)); error = y - p22Rel
p22Rel = (x*(x^2 - 15))/(3*(2*x^2 - 5)) error = 0.0000000084084014806113311713765317725998
The accuracy increases if the expansion point is a pole or zero
and OrderMode is set to relative.
Plot Accuracy of Padé Approximant
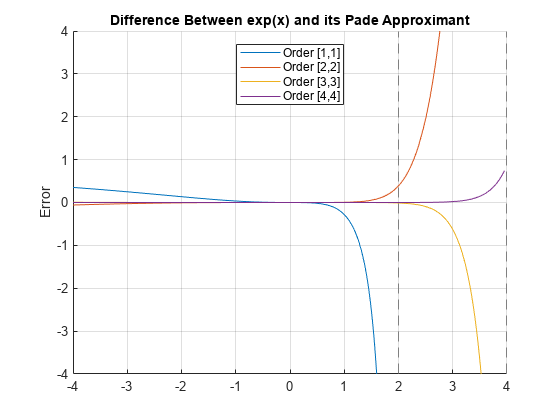
Plot the difference between exp(x) and its Padé approximants of orders [1 1] through [4 4]. Use axis to focus on the region of interest. The plot shows that accuracy increases with increasing order of the Padé approximant.
syms x expr = exp(x); hold on grid on for i = 1:4 fplot(expr - pade(expr,'Order',i)) end axis([-4 4 -4 4]) legend('Order [1,1]','Order [2,2]','Order [3,3]','Order [4,4]',... 'Location','Best') title('Difference Between exp(x) and its Pade Approximant') ylabel('Error')
Input Arguments
More About
Tips
If you use both the third argument
aandExpansionPointto specify the expansion point, the value specified viaExpansionPointprevails.
Algorithms
The parameters a1,…,bn are chosen such that the series expansion of the Padé approximant coincides with the series expansion of f to the maximal possible order.
The expansion points ±∞ and ±i∞ are not allowed.
When
padecannot find the Padé approximant, it returns the function call.For
padeto return the Padé approximant, a Taylor or Laurent series expansion of f must exist at the expansion point.
Version History
Introduced in R2014b
