ztest
z-test
Syntax
Description
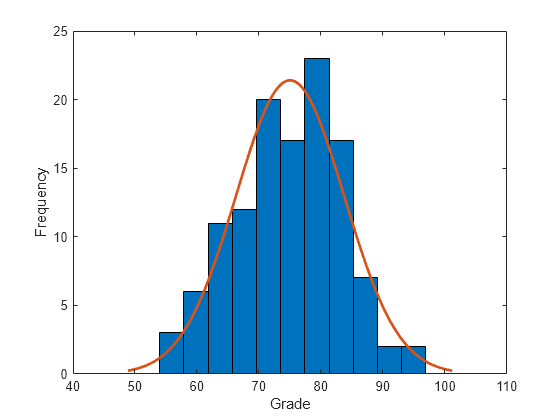
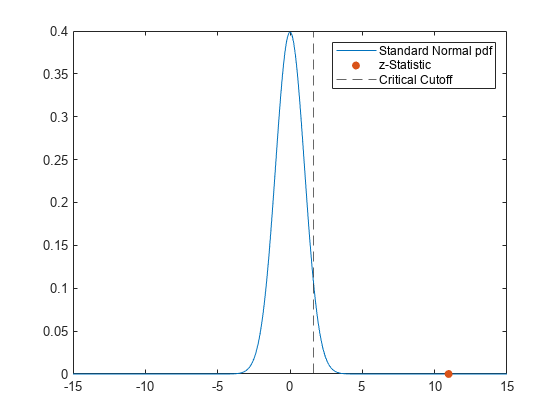
h = ztest(x,m,sigma)x comes
from a normal distribution with mean m and a
standard deviation sigma, using the z-test.
The alternative hypothesis is that the mean is not m.
The result h is 1 if the test
rejects the null hypothesis at the 5% significance level, and 0 otherwise.
h = ztest(x,m,sigma,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
Use
sampsizepwrto calculate:The sample size that corresponds to specified power and parameter values;
The power achieved for a particular sample size, given the true parameter value;
The parameter value detectable with the specified sample size and power.
Extended Capabilities
Version History
Introduced before R2006a
See Also
ttest | ttest2 | sampsizepwr