oobQuantilePredict
Quantile predictions for out-of-bag observations from bag of regression trees
Syntax
Description
YFit = oobQuantilePredict(Mdl)Mdl.X, the predictor data, and using Mdl,
which is a bag of regression trees. Mdl must be
a TreeBagger model
object and Mdl.OOBIndices must be nonempty.
YFit = oobQuantilePredict(Mdl,Name,Value)Name,Value pair
arguments. For example, specify quantile probabilities or trees to
include for quantile estimation.
[ also returns a sparse
matrix of response
weights using any of the previous syntaxes.YFit,YW]
= oobQuantilePredict(___)
Input Arguments
Name-Value Arguments
Output Arguments
Examples
More About
Algorithms
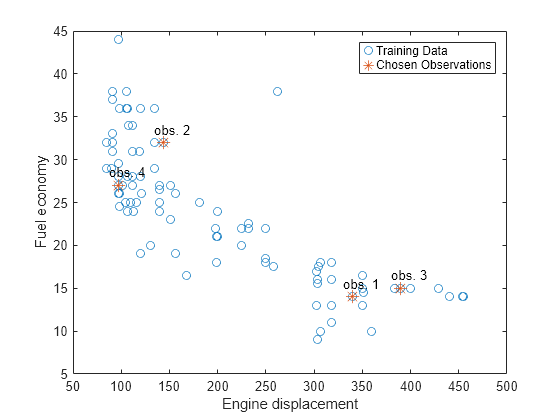
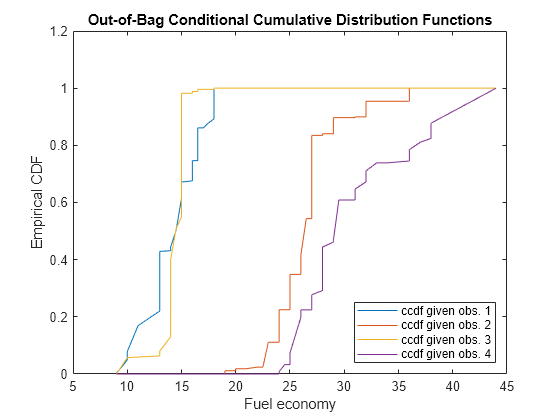
oobQuantilePredict estimates out-of-bag quantiles
by applying quantilePredict to all observations in the
training data (Mdl.X). For each observation, the
method uses only the trees for which the observation is out-of-bag.
For observations that are in-bag for all trees in the ensemble, oobQuantilePredict assigns
the sample quantile of the response data. In other words, oobQuantilePredict does
not use quantile regression for out-of-bag observations. Instead,
it assigns quantile(Mdl.Y,,
where tau)tau is the value of the Quantile name-value
pair argument.
References
[1] Meinshausen, N. “Quantile Regression Forests.” Journal of Machine Learning Research, Vol. 7, 2006, pp. 983–999.
[2] Breiman, L. “Random Forests.” Machine Learning. Vol. 45, 2001, pp. 5–32.
Version History
Introduced in R2016b