Moving Towards Automating Model Selection Using Bayesian Optimization
This example shows how to build multiple classification models for a given training data set, optimize their hyperparameters using Bayesian optimization, and select the model that performs the best on a test data set.
Training several models and tuning their hyperparameters can often take days or weeks. Creating a script to develop and compare multiple models automatically can be much faster. You can also use Bayesian optimization to speed up the process. Instead of training each model with different sets of hyperparameters, you select a few different models and tune their default hyperparameters using Bayesian optimization. Bayesian optimization finds an optimal set of hyperparameters for a given model by minimizing the objective function of the model. This optimization algorithm strategically selects new hyperparameters in each iteration and typically arrives at the optimal set of hyperparameters more quickly than a simple grid search. You can use the script in this example to train several classification models using Bayesian optimization for a given training data set and identify the model that performs best on a test data set.
Alternatively, to choose a classification model automatically across a selection of classifier types and hyperparameter values, use fitcauto. For an example, see Automated Classifier Selection with Bayesian and ASHA Optimization.
Load Sample Data
This example uses the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year. The classification task is to fit a model that predicts the salary category of people given their age, working class, education level, marital status, race, and so on.
Load the sample data census1994 and display the variables in the data set.
load census1994
whosName Size Bytes Class Attributes Description 20x74 2960 char adultdata 32561x15 1872566 table adulttest 16281x15 944466 table
census1994 contains the training data set adultdata and the test data set adulttest. For this example, to reduce the running time, subsample 5000 training and test observations each, from the original tables adultdata and adulttest, by using the datasample function. (You can skip this step if you want to use the complete data sets.)
NumSamples = 5000; s = RandStream('mlfg6331_64'); % For reproducibility adultdata = datasample(s,adultdata,NumSamples,'Replace',false); adulttest = datasample(s,adulttest,NumSamples,'Replace',false);
Preview the first few rows of the training data set.
head(adultdata)
age workClass fnlwgt education education_num marital_status occupation relationship race sex capital_gain capital_loss hours_per_week native_country salary
___ ___________ __________ ____________ _____________ __________________ _________________ ______________ _____ ______ ____________ ____________ ______________ ______________ ______
39 Private 4.91e+05 Bachelors 13 Never-married Exec-managerial Other-relative Black Male 0 0 45 United-States <=50K
25 Private 2.2022e+05 11th 7 Never-married Handlers-cleaners Own-child White Male 0 0 45 United-States <=50K
24 Private 2.2761e+05 10th 6 Divorced Handlers-cleaners Unmarried White Female 0 0 58 United-States <=50K
51 Private 1.7329e+05 HS-grad 9 Divorced Other-service Not-in-family White Female 0 0 40 United-States <=50K
54 Private 2.8029e+05 Some-college 10 Married-civ-spouse Sales Husband White Male 0 0 32 United-States <=50K
53 Federal-gov 39643 HS-grad 9 Widowed Exec-managerial Not-in-family White Female 0 0 58 United-States <=50K
52 Private 81859 HS-grad 9 Married-civ-spouse Machine-op-inspct Husband White Male 0 0 48 United-States >50K
37 Private 1.2429e+05 Some-college 10 Married-civ-spouse Adm-clerical Husband White Male 0 0 50 United-States <=50K
Each row represents the attributes of one adult, such as age, education, and occupation. The last column salary shows whether a person has a salary less than or equal to $50,000 per year or greater than $50,000 per year.
Understand Data and Choose Classification Models
Statistics and Machine Learning Toolbox™ provides several options for classification, including classification trees, discriminant analysis, naive Bayes, nearest neighbors, support vector machines (SVMs), and classification ensembles. For the complete list of algorithms, see Classification.
Before choosing the algorithms to use for your problem, inspect your data set. The census data has several noteworthy characteristics:
The data is tabular and contains both numeric and categorical variables.
The data contains missing values.
The response variable (
salary) has two classes (binary classification).
Without making any assumptions or using prior knowledge of algorithms that you expect to work well on your data, you simply train all the algorithms that support tabular data and binary classification. Error-correcting output codes (ECOC) models are used for data with more than two classes. Discriminant analysis and nearest neighbor algorithms do not analyze data that contains both numeric and categorical variables. Therefore, the algorithms appropriate for this example are SVMs, a decision tree, an ensemble of decision trees, and a naive Bayes model. Some of these models, like decision tree and naive Bayes models, are better at handling data with missing values; that is, they return non-NaN predicted scores for observations with missing values.
Build Models and Tune Hyperparameters
To speed up the process, customize the hyperparameter optimization options. Specify 'ShowPlots' as false and 'Verbose' as 0 to disable plot and message displays, respectively. Also, specify 'UseParallel' as true to run Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results.
hypopts = struct('ShowPlots',false,'Verbose',0,'UseParallel',true);
Start a parallel pool.
poolobj = gcp;
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 8 workers.
You can fit the training data set and tune parameters easily by calling each fitting function and setting its 'OptimizeHyperparameters' name-value pair argument to 'auto'. Create the classification models.
% SVMs: SVM with polynomial kernel & SVM with Gaussian kernel mdls{1} = fitcsvm(adultdata,'salary','KernelFunction','polynomial','Standardize','on', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts); mdls{2} = fitcsvm(adultdata,'salary','KernelFunction','gaussian','Standardize','on', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts); % Decision tree mdls{3} = fitctree(adultdata,'salary', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts); % Ensemble of Decision trees mdls{4} = fitcensemble(adultdata,'salary','Learners','tree', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts); % Naive Bayes mdls{5} = fitcnb(adultdata,'salary', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts);
Plot Minimum Objective Curves
Extract the Bayesian optimization results from each model and plot the minimum observed value of the objective function for each model over every iteration of the hyperparameter optimization. The objective function value corresponds to the misclassification rate measured by five-fold cross-validation using the training data set. The plot compares the performance of each model.
figure hold on N = length(mdls); for i = 1:N mdl = mdls{i}; results = mdls{i}.HyperparameterOptimizationResults; plot(results.ObjectiveMinimumTrace,'Marker','o','MarkerSize',5); end names = {'SVM-Polynomial','SVM-Gaussian','Decision Tree','Ensemble-Trees','Naive Bayes'}; legend(names,'Location','northeast') title('Bayesian Optimization') xlabel('Number of Iterations') ylabel('Minimum Objective Value')

Using Bayesian optimization to find better hyperparameter sets improves the performance of models over several iterations. In this case, the plot indicates that the ensemble of decision trees has the best prediction accuracy for the data. This model performs well consistently over several iterations and different sets of Bayesian optimization hyperparameters.
Check Performance with Test Set
Check the classifier performance with the test data set by using the confusion matrix and the receiver operating characteristic (ROC) curve.
Find the predicted labels and the score values of the test data set.
label = cell(N,1); score = cell(N,1); for i = 1:N [label{i},score{i}] = predict(mdls{i},adulttest); end
Confusion Matrix
Obtain the most likely class for each test observation by using the predict function of each model. Then compute the confusion matrix with the predicted classes and the known (true) classes of the test data set by using the confusionchart function.
figure c = cell(N,1); for i = 1:N subplot(2,3,i) c{i} = confusionchart(adulttest.salary,label{i}); title(names{i}) end
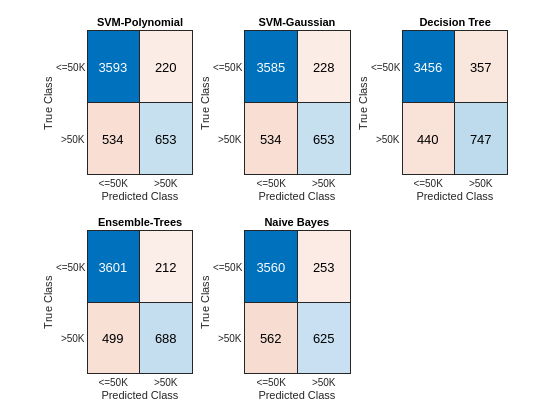
The diagonal elements indicate the number of correctly classified instances of a given class. The off-diagonal elements are instances of misclassified observations.
ROC Curve
Inspect the classifier performance more closely by plotting a ROC curve for each classifier and computing the area under the ROC curve (AUC). A ROC curve shows the true positive rate versus the false positive rate for different thresholds of classification scores. For a perfect classifier, whose true positive rate is always 1 regardless of the threshold, AUC = 1. For a binary classifier that randomly assigns observations to classes, AUC = 0.5. A large AUC value (close to 1) indicates good classifier performance.
Compute the metrics for a ROC curve and find the AUC value by creating a rocmetrics object for each classifier. Plot the ROC curves for the label '<=50K' by using the plot function of rocmetrics.
figure AUC = zeros(1,N); for i = 1:N rocObj = rocmetrics(adulttest.salary,score{i},mdls{i}.ClassNames); [r,g] = plot(rocObj,'ClassNames','<=50K'); r.DisplayName = replace(r.DisplayName,'<=50K',names{i}); g(1).DisplayName = join([names{i},' Model Operating Point']); AUC(i) = rocObj.AUC(1); hold on end title('ROC Curves for Class <=50K') hold off
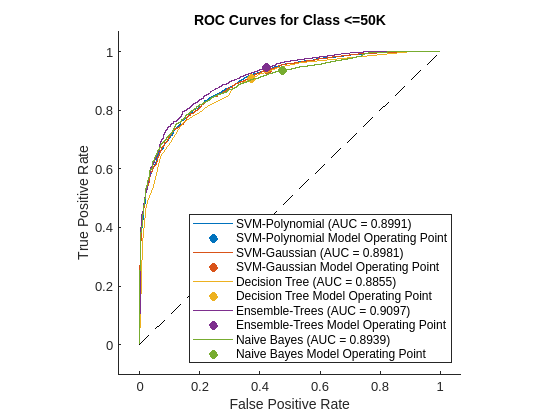
A ROC curve shows the true positive rate versus the false positive rate (or, sensitivity versus 1–specificity) for different thresholds of the classifier output.
Now plot the AUC values using a bar graph. For a perfect classifier, whose true positive rate is always 1 regardless of the thresholds, AUC = 1. For a classifier that randomly assigns observations to classes, AUC = 0.5. Larger AUC values indicate better classifier performance.
figure bar(AUC) title('Area Under the Curve') xlabel('Model') ylabel('AUC') xticklabels(names) xtickangle(30) ylim([0.85,0.925])
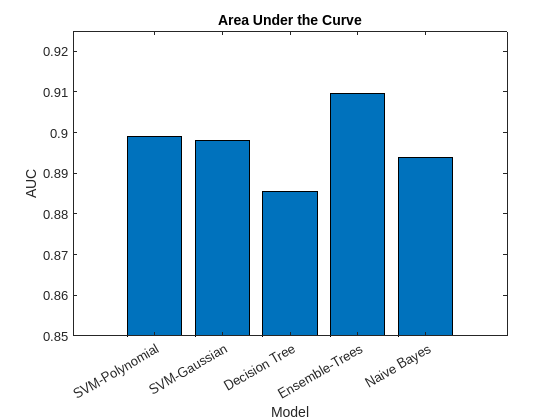
Based on the confusion matrix and the AUC bar graph, the ensemble of decision trees and SVM models achieve better accuracy than the decision tree and naive Bayes models.
Resume Optimization of Most Promising Models
Running Bayesian optimization on all models for further iterations can be computationally expensive. Instead, select a subset of models that have performed well so far and continue the optimization for 30 more iterations by using the resume function. Plot the minimum observed values of the objective function for each iteration of Bayesian optimization.
figure hold on selectedMdls = mdls([1,2,4]); newresults = cell(1,length(selectedMdls)); for i = 1:length(selectedMdls) newresults{i} = resume(selectedMdls{i}.HyperparameterOptimizationResults,'MaxObjectiveEvaluations',30); plot(newresults{i}.ObjectiveMinimumTrace,'Marker','o','MarkerSize',5) end title('Bayesian Optimization with resume') xlabel('Number of Iterations') ylabel('Minimum Objective Value') legend({'SVM-Polynomial','SVM-Gaussian','Ensemble-Trees'},'Location','northeast')
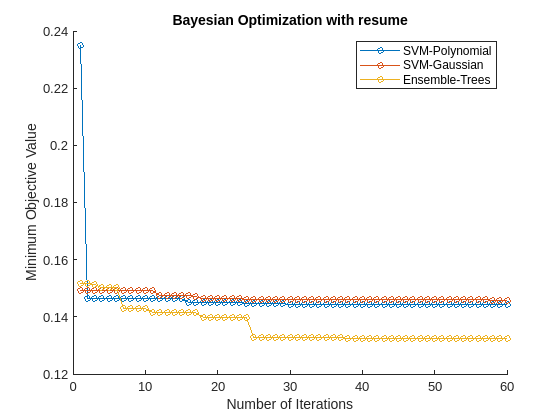
The first 30 iterations correspond to the first round of Bayesian optimization. The next 30 iterations correspond to the results of the resume function. Resuming optimization is useful because the loss continues to reduce further after the first 30 iterations.
See Also
confusionchart | perfcurve | resume | BayesianOptimization