incrementalClassificationECOC

Multiclass classification model using binary learners for incremental learning

Since R2022a

Description

The incrementalClassificationECOC function creates an incrementalClassificationECOC model object, which represents a multiclass error-correcting output codes (ECOC) classification model that uses binary learners for incremental learning.

Unlike other Statistics and Machine Learning Toolbox™ model objects, incrementalClassificationECOC can be called directly. Also, you can specify learning options, such as performance metrics configurations and prior class probabilities, before fitting the model to data. After you create an incrementalClassificationECOC object, it is prepared for incremental learning.

incrementalClassificationECOC is best suited for incremental learning. For a traditional approach to training a multiclass classification model (such as creating a model by fitting it to data, performing cross-validation, tuning hyperparameters, and so on), see fitcecoc.

Creation

You can create an incrementalClassificationECOC model object in several ways:

• Call the function directly — Configure incremental learning options, or specify learner-specific options, by calling incrementalClassificationECOC directly. This approach is best when you do not have data yet or you want to start incremental learning immediately. You must specify the maximum number of classes or all class names expected in the response data during incremental learning.

• Convert a traditionally trained model — To initialize a multiclass ECOC classification model for incremental learning using the model parameters of a trained model object (ClassificationECOC or CompactClassificationECOC), you can convert the traditionally trained model to an incrementalClassificationECOC model object by passing it to the incrementalLearner function.

• Call an incremental learning function — fit, updateMetrics, and updateMetricsAndFit accept a configured incrementalClassificationECOC model object and data as input, and return an incrementalClassificationECOC model object updated with information learned from the input model and data.

Syntax

Mdl = incrementalClassificationECOC(MaxNumClasses=maxNumClasses)

Mdl = incrementalClassificationECOC(ClassNames=classNames)

Mdl = incrementalClassificationECOC(___,Name=Value)

Description

Mdl = incrementalClassificationECOC(MaxNumClasses=maxNumClasses) returns a default incremental learning model object for multiclass ECOC classification, Mdl, where MaxNumClasses is the maximum number of classes expected in the response data during incremental learning. Properties of a default model contain placeholders for unknown model parameters. You must train a default model before you can track its performance or generate predictions from it.

Mdl = incrementalClassificationECOC(ClassNames=classNames) specifies all class names ClassNames expected in the response data during incremental learning, and sets the ClassNames property.

Mdl = incrementalClassificationECOC(___,Name=Value) uses either of the previous syntaxes to set properties and additional options using name-value arguments. For example, incrementalClassificationECOC(MaxNumClasses=5,Coding="onevsone",MetricsWarmupPeriod=100) sets the maximum number of classes expected in the response data to 5, specifies to use a one-versus-one coding design, and sets the metrics warm-up period to 100.

Input Arguments

MaxNumClasses — Maximum number of classes

positive integer

Maximum number of classes expected in the response data during incremental learning, specified as a positive integer.

MaxNumClasses sets the number of class names in the ClassNames property.

If you do not specify MaxNumClasses, you must specify the ClassNames argument.

Example: MaxNumClasses=5

Data Types: single | double

ClassNames — All unique class labels

categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

All unique class labels expected in the response data during incremental learning, specified as a categorical, character, or string array; logical or numeric vector; or cell array of character vectors. ClassNames and the response data must have the same data type. This argument sets the ClassNames property.

ClassNames specifies the order of any input or output argument dimension that corresponds to the class order. For example, set ClassNames to specify the column order of classification scores returned by predict.

If you do not specify ClassNames, you must specify the MaxNumClasses argument. In that case, the software infers the ClassNames property from the data during incremental learning.

Example: ClassNames=["virginica","setosa","versicolor"]

Data Types: single | double | logical | string | char | cell | categorical

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: NumPredictors=4,Prior=[0.3 0.3 0.4] specifies the number of predictor variables as 4 and sets the prior class probability distribution to [0.3 0.3 0.4].

Coding — Coding design

"onevsone" (default) | "allpairs" | "binarycomplete" | "denserandom" | "onevsall" | "ordinal" | "sparserandom" | "ternarycomplete" | numeric matrix

Coding design name, specified as a numeric matrix or a value in this table.

Value	Number of Binary Learners	Description
"allpairs" and "onevsone"	K(K – 1)/2	For each binary learner, one class is positive, another is negative, and the software ignores the rest. This design exhausts all combinations of class pair assignments.
"binarycomplete"	$$2^{(K-1)}-1$$	This design partitions the classes into all binary combinations, and does not ignore any classes. For each binary learner, all class assignments are –1 and 1 with at least one positive class and one negative class in the assignment.
"denserandom"	Random, but approximately 10 log2K	For each binary learner, the software randomly assigns classes into positive or negative classes, with at least one of each type. For more details, see Random Coding Design Matrices.
"onevsall"	K	For each binary learner, one class is positive and the rest are negative. This design exhausts all combinations of positive class assignments.
"ordinal"	K – 1	For the first binary learner, the first class is negative and the rest are positive. For the second binary learner, the first two classes are negative and the rest are positive, and so on.
"sparserandom"	Random, but approximately 15 log2K	For each binary learner, the software randomly assigns classes as positive or negative with probability 0.25 for each, and ignores classes with probability 0.5. For more details, see Random Coding Design Matrices.
"ternarycomplete"	$$\left(3^K-2^{(K+1)}+1\right)/2$$	This design partitions the classes into all ternary combinations. All class assignments are 0, –1, and 1 with at least one positive class and one negative class in each assignment.

You can also specify a coding design using a custom coding matrix, which is a K-by-L matrix. Each row corresponds to a class and each column corresponds to a binary learner. The class order (rows) corresponds to the order in the ClassNames property. Create the matrix by following these guidelines:

• Every element of the custom coding matrix must be –1, 0, or 1, and the value must correspond to a dichotomous class assignment. Consider Coding(i,j), the class that learner j assigns to observations in class i.

  Value	Dichotomous Class Assignment
  –1	Learner j assigns observations in class i to a negative class.
  0	Before training, learner j removes observations in class i from the data set.
  1	Learner j assigns observations in class i to a positive class.

• Every column must contain at least one –1 and one 1.

• For all column indices i,j where i ≠ j, Coding(:,i) cannot equal Coding(:,j), and Coding(:,i) cannot equal –Coding(:,j).

• All rows of the custom coding matrix must be different.

For more details on the form of custom coding design matrices, see Custom Coding Design Matrices.

Example: Coding="ternarycomplete"

Data Types: char | string | double | single | int16 | int32 | int64 | int8

Metrics — Model performance metrics to track during incremental learning

"classiferror" (default) | function handle | cell vector | structure array

Model performance metrics to track during incremental learning, specified as "classiferror" (classification error, or misclassification error rate), a function handle (for example, @metricName), a structure array of function handles, or a cell vector of names, function handles, or structure arrays.

When Mdl is warm (see IsWarm), updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of Mdl.

To specify a custom function that returns a performance metric, use function handle notation. The function must have this form.

metric = customMetric(C,S)

• The output argument metric is an n-by-1 numeric vector, where each element is the loss of the corresponding observation in the data processed by the incremental learning functions during a learning cycle.

• You specify the function name (here, customMetric).

• C is an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs, where K is the number of classes. The column order corresponds to the class order in the ClassNames property. Create C by setting C(p,q) = 1, if observation p is in class q, for each observation in the specified data. Set the other element in row p to 0.

• S is an n-by-K numeric matrix of predicted classification scores. S is similar to the NegLoss output of predict, where rows correspond to observations in the data and the column order corresponds to the class order in the ClassNames property. S(p,q) is the classification score of observation p being classified in class q.

To specify multiple custom metrics and assign a custom name to each, use a structure array. To specify a combination of built-in and custom metrics, use a cell vector.

updateMetrics and updateMetricsAndFit store specified metrics in a table in the Metrics property. The data type of Metrics determines the row names of the table.

Metrics Value Data Type	Description of Metrics Property Row Name	Example
String or character vector	Name of corresponding built-in metric	Row name for "classiferror" is "ClassificationError"
Structure array	Field name	Row name for struct(Metric1=@customMetric1) is "Metric1"
Function handle to function stored in a program file	Name of function	Row name for @customMetric is "customMetric"
Anonymous function	CustomMetric_j, where j is metric j in Metrics	Row name for @(C,S)customMetric(C,S)... is CustomMetric_1

For more details on performance metrics options, see Performance Metrics.

Example: Metrics=struct(Metric1=@customMetric1,Metric2=@customMetric2)

Example: Metrics={@customMetric1,@customMetric2,"classiferror",struct(Metric3=@customMetric3)}

Data Types: char | string | struct | cell | function_handle

Learners — Binary learner templates

"linear" (default) | "kernel" | incremental learning object | template object | cell array of incremental learning objects and template objects

Binary learner templates, specified as "linear", "kernel", an incremental learning object, a template object, or a cell array of supported incremental learning objects and template objects.

• "linear" or "kernel" — Specify the Learners value as a string scalar or character vector to use the default linear learners or default kernel learners (default incrementalClassificationLinear or incrementalClassificationKernel objects, respectively).

• Incremental learning object (incrementalClassificationLinear or incrementalClassificationKernel object) — Configure binary learner properties (both model-specific properties and incremental learning properties) when you create an incremental learning object, and pass the object to incrementalClassificationECOC as the Learners value.

• Template object returned by the templateLinear, templateSVM, or templateKernel function — Configure model-specific properties when you create a template object, and pass the object to incrementalClassificationECOC as the Learners value. Use this approach to specify model properties with a template object and to use the default incremental learning options.

• Cell array of supported incremental learning objects and template objects — Use this approach to customize each learner individually.

You cannot specify the ClassNames (class names) and Prior (prior class probabilities) properties for an incrementalClassificationECOC object by using the binary learners. Instead, specify the properties by using the corresponding name-value arguments of incrementalClassificationECOC.

Example: Learners="kernel"

UpdateBinaryLearnerMetrics — Flag for updating metrics of binary learners

false or 0 (default) | true or 1

Flag for updating the metrics of binary learners, specified as logical 0 (false) or 1 (true).

If the value is true, the software tracks the performance metrics of binary learners using the Metrics property of the binary learners, stored in the BinaryLearners property. For an example, see Configure Incremental Model to Track Performance Metrics for Model and Binary Learners.

Example: UpdateBinaryLearnerMetrics=true

Data Types: logical

Properties

You can set most properties by using name-value argument syntax when you call incrementalClassificationECOC directly. You cannot set the properties BinaryLearners, CodingMatrix, CodingName, NumTrainingObservations, and IsWarm using name-value argument syntax with the arguments of the same names. However, you can set CodingMatrix and CodingName by using the Coding name-value argument, and you can set BinaryLearners by using the Learners name-value argument.

You can set some properties when you call incrementalLearner to convert a traditionally trained model.

Classification Model Parameters

BinaryLearners — Trained binary learners

Read-only: cell array of model objects

This property is read-only.

Trained binary learners, specified as a cell array of incrementalClassificationLinear or incrementalClassificationKernel model objects. The number of binary learners depends on the coding design.

The software trains BinaryLearner{j} according to the binary problem specified by CodingMatrix(:,j).

The default BinaryLearners value depends on how you create the model:

• If you convert a traditionally trained model (for example, TTMdl) to create Mdl, BinaryLearners contains incremental learners converted from the binary learners in TTMdl.

  When you train TTMdl, you must specify the Learners name-value argument of fitcecoc to use support vector machine (SVM) binary learner templates (templateSVM) or linear classification model binary learner templates (templateLinear).

• Otherwise, the Learners name-value argument sets this property. The default value of the argument is "linear", which uses incrementalClassificationLinear model objects with SVM learners.

Data Types: cell

BinaryLoss — Binary learner loss function

Read-only: "hamming" | "linear" | "logit" | "exponential" | "binodeviance" | "hinge" | "quadratic" | function handle

This property is read-only.

Binary learner loss function, specified as a built-in loss function name or function handle. incrementalClassificationECOC stores the BinaryLoss value as a character vector or function handle.

• This table describes the built-in functions, where y_j is the class label for a particular binary learner (in the set {–1,1,0}), s_j is the score for observation j, and g(y_j,s_j) is the binary loss formula.

  Value	Description	Score Domain	g(yj,sj)
  "binodeviance"	Binomial deviance	(–∞,∞)	log[1 + exp(–2yjsj)]/[2log(2)]
  "exponential"	Exponential	(–∞,∞)	exp(–yjsj)/2
  "hamming"	Hamming	[0,1] or (–∞,∞)	[1 – sign(yjsj)]/2
  "hinge"	Hinge	(–∞,∞)	max(0,1 – yjsj)/2
  "linear"	Linear	(–∞,∞)	(1 – yjsj)/2
  "logit"	Logistic	(–∞,∞)	log[1 + exp(–yjsj)]/[2log(2)]
  "quadratic"	Quadratic	[0,1]	[1 – yj(2sj – 1)]2/2

  The software normalizes binary losses so that the loss is 0.5 when y_j = 0. Also, the software calculates the mean binary loss for each class [1].

• For a custom binary loss function, for example customFunction, specify its function handle BinaryLoss=@customFunction.

  customFunction has this form:

  bLoss = customFunction(M,s)

  • M is the K-by-B coding matrix stored in Mdl.CodingMatrix.

  • s is the 1-by-B row vector of classification scores.

  • bLoss is the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.

  • K is the number of classes.

  • B is the number of binary learners.

  For an example of a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function. This example is for a traditionally trained model. You can define a custom loss function for incremental learning as shown in the example.

For more information, see Binary Loss.

The default BinaryLoss value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, BinaryLoss is specified by the corresponding property of the traditionally trained model. You can also specify the BinaryLoss value by using the BinaryLoss name-value argument of incrementalLearner.

• Otherwise, the default value of BinaryLoss is "hinge".

Data Types: char | string | function_handle

ClassNames — All unique class labels

Read-only: categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

This property is read-only.

All unique class labels expected in the response data during incremental learning, specified as a categorical or character array, a logical or numeric vector, or a cell array of character vectors.

You can set ClassNames in one of three ways:

• If you specify the MaxNumClasses argument, the software infers the ClassNames property during incremental learning.

• If you specify the ClassNames argument, incrementalClassificationECOC stores your specification in the ClassNames property. (The software treats string arrays as cell arrays of character vectors.)

• If you convert a traditionally trained model to create Mdl, the ClassNames property is specified by the corresponding property of the traditionally trained model.

Data Types: single | double | logical | char | string | cell | categorical

CodingMatrix — Class assignment codes

Read-only: numeric matrix

This property is read-only.

Class assignment codes for the binary learners, specified as a numeric matrix. CodingMatrix is a K-by-L matrix, where K is the number of classes and L is the number of binary learners.

The elements of CodingMatrix are –1, 0, and 1, and the values correspond to dichotomous class assignments. This table describes how learner j assigns observations in class i to a dichotomous class corresponding to the value of CodingMatrix(i,j).

Value	Dichotomous Class Assignment
–1	Learner j assigns observations in class i to a negative class.
0	Before training, learner j removes observations in class i from the data set.
1	Learner j assigns observations in class i to a positive class.

For details, see Coding Design.

The default CodingMatrix value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, CodingMatrix is specified by the corresponding property of the traditionally trained model.

• Otherwise, the Coding name-value argument sets this property. The default value of the argument uses the one-versus-one coding design.

Data Types: double | single | int8 | int16 | int32 | int64

CodingName — Coding design name

Read-only: character vector

This property is read-only.

Coding design name, specified as a character vector.

The default CodingName value depends on how you create the model:

• If you convert a full, traditionally trained model (ClassificationECOC) to create Mdl, CodingName is specified by the corresponding property of the traditionally trained model.

• If you convert a compact, traditionally trained model (CompactClassificationECOC) to create Mdl, CodingName is "converted".

• Otherwise, the Coding name-value argument sets this property. The default value of the argument is "onevsone". If you specify a custom coding matrix using Coding, CodingName is "custom".

For details, see Coding Design.

Data Types: char

Decoding — Decoding scheme

Read-only: "lossweighted" | "lossbased"

This property is read-only.

Decoding scheme, specified as "lossweighted" or "lossbased". incrementalClassificationECOC stores the Decoding value as a character vector.

The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation. The software supports two decoding schemes:

• "lossweighted" — The predicted class of an observation corresponds to the class that produces the minimum sum of the binary losses over binary learners.

• "lossbased" — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over binary learners.

For more information, see Binary Loss.

The default Decoding value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the Decoding name-value argument of incrementalLearner sets this property. The default value of the argument is "lossweighted".

• Otherwise, the default value of Decoding is "lossweighted".

Data Types: char | string

NumPredictors — Number of predictor variables

Read-only: nonnegative numeric scalar

This property is read-only.

Number of predictor variables, specified as a nonnegative numeric scalar.

The default NumPredictors value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, NumPredictors is specified by the corresponding property of the traditionally trained model.

• If you create Mdl by calling incrementalClassificationECOC directly, you can specify NumPredictors by using name-value argument syntax. If you do not specify the value, then the default value is 0, and incremental fitting functions infer NumPredictors from the predictor data during training.

Data Types: double

NumTrainingObservations — Number of observations fit to incremental model

Read-only: 0 (default) | nonnegative numeric scalar

This property is read-only.

Number of observations fit to the incremental model Mdl, specified as a nonnegative numeric scalar. NumTrainingObservations increases when you pass Mdl and training data to fit or updateMetricsAndFit.

Note

If you convert a traditionally trained model to create Mdl, incrementalClassificationECOC does not add the number of observations fit to the traditionally trained model to NumTrainingObservations.

Data Types: double

Prior — Prior class probabilities

Read-only: numeric vector | "empirical" | "uniform"

This property is read-only.

Prior class probabilities, specified as "empirical", "uniform", or a numeric vector. incrementalClassificationECOC stores the Prior value as a numeric vector.

Value	Description
"empirical"	Incremental learning functions infer prior class probabilities from the observed class relative frequencies in the response data during incremental training.
"uniform"	For each class, the prior probability is 1/K, where K is the number of classes.
numeric vector	Custom, normalized prior probabilities. The order of the elements of Prior corresponds to the elements of the ClassNames property.

The default Prior value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, Prior is specified by the corresponding property of the traditionally trained model.

• Otherwise, the default value is "empirical".

Data Types: single | double | char | string

ScoreTransform — Score transformation function to apply to predicted scores

Read-only: 'none'

This property is read-only.

Score transformation function to apply to the predicted scores, specified as 'none'. An ECOC model does not support score transformation.

Performance Metrics Parameters

IsWarm — Flag indicating whether model tracks performance metrics

false or 0 | true or 1

Flag indicating whether the incremental model tracks performance metrics, specified as logical 0 (false) or 1 (true).

The incremental model Mdl is warm (IsWarm becomes true) when incremental fitting functions perform both of these actions:

• Fit the incremental model to MetricsWarmupPeriod observations.

• Process MaxNumClasses classes or all class names specified by the ClassNames name-value argument.

Value	Description
true or 1	The incremental model Mdl is warm. Consequently, updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of Mdl.
false or 0	updateMetrics and updateMetricsAndFit do not track performance metrics.

Data Types: logical

Metrics — Model performance metrics

Read-only: table

This property is read-only.

Model performance metrics updated during incremental learning by updateMetrics and updateMetricsAndFit, specified as a table with two columns and m rows, where m is the number of metrics specified by the Metrics name-value argument.

The columns of Metrics are labeled Cumulative and Window.

• Cumulative: Element j is the model performance, as measured by metric j, from the time the model became warm (IsWarm is 1).

• Window: Element j is the model performance, as measured by metric j, evaluated over all observations within the window specified by the MetricsWindowSize property. The software updates Window after it processes MetricsWindowSize observations.

Rows are labeled by the specified metrics. For details, see the Metrics name-value argument of incrementalLearner or incrementalClassificationECOC.

Data Types: table

MetricsWarmupPeriod — Number of observations fit before tracking performance metrics

Read-only: nonnegative integer

This property is read-only.

Number of observations the incremental model must be fit to before it tracks performance metrics in its Metrics property, specified as a nonnegative integer.

The default MetricsWarmupPeriod value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the MetricsWarmupPeriod name-value argument of the incrementalLearner function sets this property. The default value of the argument is 0.

• Otherwise, the default value is 1000.

For more details, see Performance Metrics.

Data Types: single | double

MetricsWindowSize — Number of observations to use to compute window performance metrics

Read-only: positive integer

This property is read-only.

Number of observations to use to compute window performance metrics, specified as a positive integer.

The default MetricsWindowSize value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the MetricsWindowSize name-value argument of the incrementalLearner function sets this property. The default value of the argument is 200.

• Otherwise, the default value is 200.

For more details on performance metrics options, see Performance Metrics.

Data Types: single | double

Object Functions

fit	Train ECOC classification model for incremental learning
updateMetricsAndFit	Update performance metrics in ECOC incremental learning classification model given new data and train model
updateMetrics	Update performance metrics in ECOC incremental learning classification model given new data
loss	Loss of ECOC incremental learning classification model on batch of data
predict	Predict responses for new observations from ECOC incremental learning classification model
perObservationLoss	Per observation classification error of model for incremental learning
reset	Reset incremental classification model

Examples

Create Incremental Learner with Little Prior Information

To create an ECOC classification model for incremental learning, you must specify the maximum number of classes that you expect the model to process (MaxNumClasses name-value argument). As you fit the model to incoming batches of data by using an incremental fitting function, the model collects new classes in its ClassNames property. If the specified maximum number of classes is inaccurate, one of the following occurs:

• Before an incremental fitting function processes the expected maximum number of classes, the model is cold. Consequently, the updateMetrics and updateMetricsAndFit functions do not measure performance metrics.

• If the number of classes exceeds the maximum expected, the incremental fitting function issues an error.

This example shows how to create an ECOC model for incremental learning when the only information you specify is the expected maximum number of classes in the data. Also, the example illustrates the consequences when incremental fitting functions process all expected classes early and late in the sample.

For this example, consider training a device to predict whether a subject is sitting, standing, walking, running, or dancing based on biometric data measured on the subject. Therefore, the device has a maximum of 5 classes from which to choose.

Process Expected Maximum Number of Classes Early in Sample

Load the human activity data set. Randomly shuffle the data.

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

For details on the data set, enter Description at the command line.

Create an incremental ECOC model for multiclass learning. Specify a maximum of 5 classes in the data.

MdlEarly = incrementalClassificationECOC(MaxNumClasses=5)

MdlEarly = 
  incrementalClassificationECOC

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'none'
    BinaryLearners: {10×1 cell}
        CodingName: 'onevsone'
          Decoding: 'lossweighted'


  Properties, Methods

MdlEarly is an incrementalClassificationECOC model object. All its properties are read-only. MdlEarly must be fit to data before you can use it to perform any other operations.

Display the coding design matrix.

MdlEarly.CodingMatrix

ans = 5×10

     1     1     1     1     0     0     0     0     0     0
    -1     0     0     0     1     1     1     0     0     0
     0    -1     0     0    -1     0     0     1     1     0
     0     0    -1     0     0    -1     0    -1     0     1
     0     0     0    -1     0     0    -1     0    -1    -1

Each row of the coding design matrix corresponds to a class, and each column corresponds to a binary learner. For example, the first binary learner is for classes 1 and 2, and the fourth binary learner is for classes 1 and 5, where both learners assume class 1 as a positive class.

Fit the incremental model to the training data by using the updateMetricsAndFit function. Simulate a data stream by processing chunks of 50 observations at a time. At each iteration:

• Process 50 observations.

• Overwrite the previous incremental model with a new one fitted to the incoming observations.

• Store the first model coefficient of the first binary learner $${\beta }_{11}$$, the cumulative metrics, and the window metrics to see how they evolve during incremental learning.

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
mc = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
beta11 = zeros(nchunk+1,1);    

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    MdlEarly = updateMetricsAndFit(MdlEarly,X(idx,:),Y(idx));
    mc{j,:} = MdlEarly.Metrics{"ClassificationError",:};
    beta11(j) = MdlEarly.BinaryLearners{1}.Beta(1);
end

MdlEarly is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.

To see how the performance metrics and $${\beta }_{11}$$ evolve during training, plot them on separate tiles.

t = tiledlayout(2,1);
nexttile
plot(beta11)
ylabel("\beta_{11}")
xlim([0 nchunk])
nexttile
plot(mc.Variables)
xlim([0 nchunk])
ylabel("Classification Error")
xline(MdlEarly.MetricsWarmupPeriod/numObsPerChunk,"--")
legend(mc.Properties.VariableNames)
xlabel(t,"Iteration")

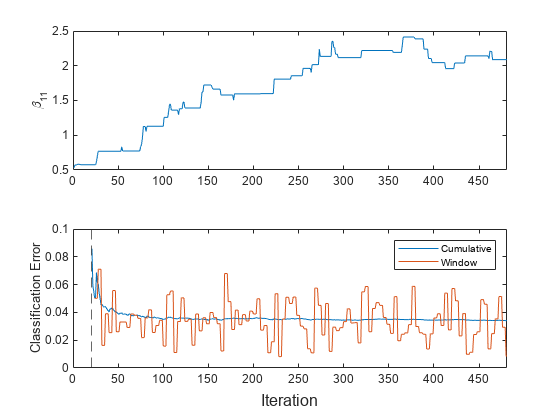
The plots indicate that updateMetricsAndFit performs the following actions:

• Fit $${\beta }_{11}$$ during all incremental learning iterations.

• Compute the performance metrics after the metrics warm-up period (dashed vertical line) only.

• Compute the cumulative metrics during each iteration.

• Compute the window metrics after processing 200 observations (4 iterations).

Process Expected Maximum Number of Classes Late in Sample

Rearrange the data set so that only the last 5000 samples contain the observations labeled with class 5.

Move all observations labeled with class 5 to the end of the sample.

idx5 = Y == 5;
Xnew = [X(~idx5,:); X(idx5,:)];
Ynew = [Y(~idx5); Y(idx5)];
sum(idx5)

ans = 
2653

Shuffle the last 5000 samples.

m = 5000;
idx_shuffle = randsample(m,m);
Xnew(end-m+1:end,:) = Xnew(end-m+idx_shuffle,:);
Ynew(end-m+1:end) = Ynew(end-m+idx_shuffle);

An ECOC model trains a binary learner only when an incoming chunk contains observations for the classes that the binary learner treats as either positive or negative. Therefore, when the labels in incoming data are not well distributed for all expected classes, a good practice is to choose a coding design that does not have zeros in the coding matrix so that the software trains all binary learners for every chunk.

Create a new ECOC model for incremental learning. Specify the onevsall coding design. In this design, one class is positive and the rest are negative for each binary learner.

MdlLate = incrementalClassificationECOC(MaxNumClasses=5,Coding="onevsall")

MdlLate = 
  incrementalClassificationECOC

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'none'
    BinaryLearners: {5×1 cell}
        CodingName: 'onevsall'
          Decoding: 'lossweighted'


  Properties, Methods

Display the coding design matrix.

MdlLate.CodingMatrix

ans = 5×5

     1    -1    -1    -1    -1
    -1     1    -1    -1    -1
    -1    -1     1    -1    -1
    -1    -1    -1     1    -1
    -1    -1    -1    -1     1

Fit the incremental model and plot the results. Store the first model coefficients of the first and fifth binary learners, $${\beta }_{11}$$ and $${\beta }_{51}$$.

mcnew = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
beta11new = zeros(nchunk,1);    
beta51new = zeros(nchunk,1); 

for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    MdlLate = updateMetricsAndFit(MdlLate,Xnew(idx,:),Ynew(idx));
    mcnew{j,:} = MdlLate.Metrics{"ClassificationError",:};
    beta11new(j) = MdlLate.BinaryLearners{1}.Beta(1);
    beta51new(j) = MdlLate.BinaryLearners{5}.Beta(1);
end

t = tiledlayout(3,1);
nexttile
plot(beta11new)
xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,"--")
xline((n-m)/numObsPerChunk,":")
ylabel("\beta_{11}")
xlim([0 nchunk])
nexttile
plot(beta51new)
xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,"--")
xline((n-m)/numObsPerChunk,":")
ylabel("\beta_{51}")
xlim([0 nchunk])
nexttile
plot(mcnew.Variables)
xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,"--")
xline((n-m)/numObsPerChunk,":")
xlim([0 nchunk])
ylabel("Classification Error")
legend(mcnew.Properties.VariableNames,Location="best")
xlabel(t,"Iteration")

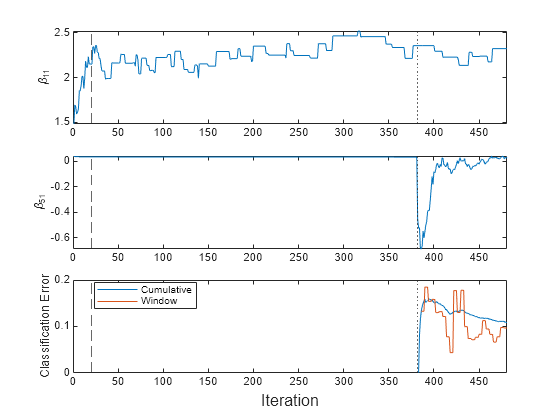
The updateMetricsAndFit function trains the model throughout incremental learning. However, $${\beta }_{51}$$ does not change significantly until an incoming chunk contains observations with the fifth class (the dotted vertical line). Also, the function starts tracking performance metrics only after the model is fit to the expected number of classes.

Specify All Class Names

Create an incremental ECOC model when you know all the class names in the data.

Consider training a device to predict whether a subject is sitting, standing, walking, running, or dancing based on biometric data measured on the subject. The class names map 1 through 5 to an activity.

Create an incremental ECOC model for multiclass learning. Specify the class names.

classnames = 1:5;
Mdl = incrementalClassificationECOC(ClassNames=classnames)

Mdl = 
  incrementalClassificationECOC

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1 2 3 4 5]
    ScoreTransform: 'none'
    BinaryLearners: {10×1 cell}
        CodingName: 'onevsone'
          Decoding: 'lossweighted'


  Properties, Methods

Mdl is an incrementalClassificationECOC model object. All its properties are read-only.

Mdl must be fit to data before you can use it to perform any other operations.

Load the human activity data set. Randomly shuffle the data.

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

For details on the data set, enter Description at the command line.

Fit the incremental model to the training data by using the updateMetricsAndFit function. Simulate a data stream by processing chunks of 50 observations at a time. At each iteration:

• Process 50 observations.

• Overwrite the previous incremental model with a new one fitted to the incoming observations.

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,X(idx,:),Y(idx));
end

Configure Incremental Learning Options

In addition to specifying the maximum number of classes, prepare an incremental ECOC learner by specifying a metrics warm-up period and a metrics window size.

Load the human activity data set. Randomly shuffle the data. Orient the observations of the predictor data in columns.

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:)';
Y = actid(idx);

For details on the data set, enter Description at the command line.

Create an incremental ECOC model for multiclass learning. Configure the model as follows:

• Set the maximum number of classes to 5.

• Specify a metrics warm-up period of 5000 observations.

• Specify a metrics window size of 500 observations.

Mdl = incrementalClassificationECOC(MaxNumClasses=5, ...
    MetricsWarmupPeriod=5000,MetricsWindowSize=500)

Mdl = 
  incrementalClassificationECOC

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'none'
    BinaryLearners: {10×1 cell}
        CodingName: 'onevsone'
          Decoding: 'lossweighted'


  Properties, Methods

Mdl is an incrementalClassificationECOC model object configured for incremental learning. By default, incrementalClassificationECOC uses classification error loss to measure the performance of the model.

Fit the incremental model to the rest of the data by using the updateMetricsAndFit function. At each iteration:

• Simulate a data stream by processing a chunk of 50 observations.

• Overwrite the previous incremental model with a new one fitted to the incoming observations. Specify that the observations are oriented in columns.

• Store the first model coefficient of the first binary learner $${\beta }_{11}$$, the cumulative metrics, and the window metrics to see how they evolve during incremental learning.

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ce = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
beta11 = zeros(nchunk,1);    

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,X(:,idx),Y(idx),ObservationsIn="columns");
    ce{j,:} = Mdl.Metrics{"ClassificationError",:};
    beta11(j) = Mdl.BinaryLearners{1}.Beta(1);
end

Mdl is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.

To see how the performance metrics and $${\beta }_{11}$$ evolve during training, plot them on separate tiles.

t = tiledlayout(2,1);
nexttile
plot(beta11)
ylabel("\beta_{11}")
xlim([0 nchunk])
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--")
nexttile
plot(ce.Variables)
xlim([0 nchunk])
ylabel("Classification Error")
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--")
legend(ce.Properties.VariableNames)
xlabel(t,"Iteration")

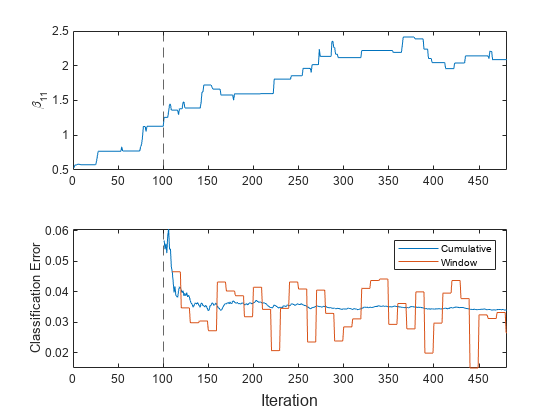
The plots indicate that updateMetricsAndFit performs the following actions:

• Fit $${\beta }_{11}$$ during all incremental learning iterations.

• Compute the performance metrics after the metrics warm-up period (dashed vertical line) only.

• Compute the cumulative metrics during each iteration.

• Compute the window metrics after processing 500 observations (10 iterations).

Convert Traditionally Trained Model to Incremental Learner

Train an ECOC model for multiclass classification by using fitcecoc. Then, convert the model to an incremental learner, track its performance, and fit the model to streaming data. Carry over training options from traditional to incremental learning.

Load and Preprocess Data

Load the human activity data set. Randomly shuffle the data.

load humanactivity
rng(1) % For reproducibility
n = numel(actid);
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

For details on the data set, enter Description at the command line.

Suppose that the data collected when the subject was stationary (Y <= 2) has double the quality than when the subject was moving. Create a weight variable that attributes 2 to observations collected from a stationary subject, and 1 to a moving subject.

W = ones(n,1) + (Y <= 2);

Train ECOC Model

Fit an ECOC model for multiclass classification to a random sample of half the data.

idxtt = randsample([true false],n,true);
TTMdl = fitcecoc(X(idxtt,:),Y(idxtt),Weights=W(idxtt))

TTMdl = 
  ClassificationECOC
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: [1 2 3 4 5]
           ScoreTransform: 'none'
           BinaryLearners: {10×1 cell}
               CodingName: 'onevsone'


  Properties, Methods

TTMdl is a ClassificationECOC model object representing a traditionally trained ECOC model.

Convert Trained Model

Convert the traditionally trained ECOC model to a model for incremental learning.

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalClassificationECOC

            IsWarm: 1
           Metrics: [1×2 table]
        ClassNames: [1 2 3 4 5]
    ScoreTransform: 'none'
    BinaryLearners: {10×1 cell}
        CodingName: 'onevsone'
          Decoding: 'lossweighted'


  Properties, Methods

IncrementalMdl is an incrementalClassificationECOC model object configured for incremental learning.

Separately Track Performance Metrics and Fit Model

Perform incremental learning on the rest of the data by using the updateMetrics and fit functions. Simulate a data stream by processing 50 observations at a time. At each iteration:

1. Call updateMetrics to update the cumulative and window classification error of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the Metrics property. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model. Specify the observation weights.

2. Call fit to fit the model to the incoming chunk of observations. Overwrite the previous incremental model to update the model parameters. Specify the observation weights.

3. Store the classification error and first model coefficient of the first binary learner $${\beta }_{11}$$.

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 50;
nchunk = floor(nil/numObsPerChunk);
ec = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
beta11 = [IncrementalMdl.BinaryLearners{1}.Beta(1); zeros(nchunk+1,1)];
Xil = X(idxil,:);
Yil = Y(idxil);
Wil = W(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx), ...
        Weights=Wil(idx));
    ec{j,:} = IncrementalMdl.Metrics{"ClassificationError",:};
    IncrementalMdl = fit(IncrementalMdl,Xil(idx,:),Yil(idx),Weights=Wil(idx));
    beta11(j+1) = IncrementalMdl.BinaryLearners{1}.Beta(1);
end

IncrementalMdl is an incrementalClassificationECOC model object trained on all the data in the stream.

Alternatively, you can use updateMetricsAndFit to update the performance metrics of the model given a new chunk of data, and then fit the model to the data.

Plot a trace plot of the performance metrics and estimated coefficient $${\beta }_{11}$$ on separate tiles.

t = tiledlayout(2,1);
nexttile
plot(ec.Variables)
xlim([0 nchunk])
ylabel("Classification Error")
legend(ec.Properties.VariableNames)
nexttile
plot(beta11)
ylabel("\beta_{11}")
xlim([0 nchunk])
xlabel(t,"Iteration")

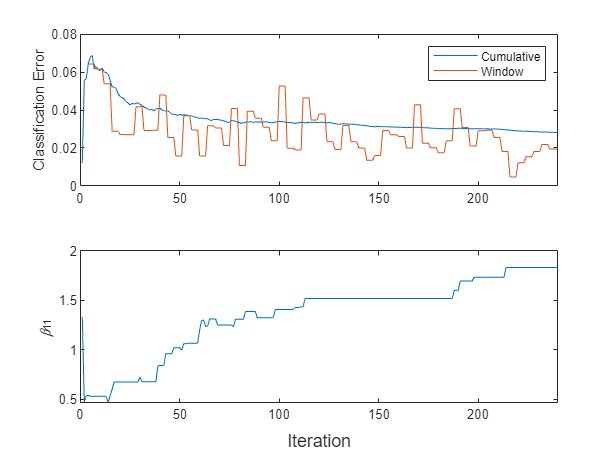
The cumulative loss levels quickly and is stable, whereas the window loss jumps throughout the training.

$${\beta }_{11}$$ changes abruptly at first, then gradually levels off as fit processes more chunks.

Specify Binary Learners

Customize binary learners of an incrementalClassificationECOC model object by specifying the Learners name-value argument.

First, configure binary learner properties by creating an incrementalClassificationLinear object. Set the linear classification model type (Learner) to logistic regression, and specify Standardize as true to standardize the predictor data.

binaryMdl = incrementalClassificationLinear(Learner="logistic", ...
    Standardize=true)

binaryMdl = 
  incrementalClassificationLinear

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'logit'
              Beta: [0×1 double]
              Bias: 0
           Learner: 'logistic'


  Properties, Methods

Create an incremental ECOC model for multiclass learning. Specify the number of classes in the data as five, and set the binary learner template (Learners) to binaryMdl.

Mdl = incrementalClassificationECOC(MaxNumClasses=5,Learners=binaryMdl)

Mdl = 
  incrementalClassificationECOC

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'none'
    BinaryLearners: {10×1 cell}
        CodingName: 'onevsone'
          Decoding: 'lossweighted'


  Properties, Methods

Display the BinaryLearners property in Mdl.

Mdl.BinaryLearners

ans=10×1 cell array
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}
    {1×1 incrementalClassificationLinear}

By default, incrementalClassificationECOC uses the one-versus-one coding design, which requires 10 learners for five classes. Therefore, the BinaryLearners property contains 10 binary learners of type incrementalClassificationLinear.

More About

Incremental Learning

Incremental learning, or online learning, is a branch of machine learning concerned with processing incoming data from a data stream, possibly given little to no knowledge of the distribution of the predictor variables, aspects of the prediction or objective function (including tuning parameter values), or whether the observations are labeled. Incremental learning differs from traditional machine learning, where enough labeled data is available to fit to a model, perform cross-validation to tune hyperparameters, and infer the predictor distribution.

Given incoming observations, an incremental learning model processes data in any of the following ways, but usually in this order:

• Predict labels.

• Measure the predictive performance.

• Check for structural breaks or drift in the model.

• Fit the model to the incoming observations.

For more details, see Incremental Learning Overview.

Adaptive Scale-Invariant Solver for Incremental Learning

The adaptive scale-invariant solver for incremental learning, introduced in [5], is a gradient-descent-based objective solver for training linear predictive models. The solver is hyperparameter free, insensitive to differences in predictor variable scales, and does not require prior knowledge of the distribution of the predictor variables. These characteristics make it well suited to incremental learning.

The incremental fitting functions fit and updateMetricsAndFit use the more aggressive ScInOL2 version of the algorithm to train binary learners. The functions always shuffles an incoming batch of data before fitting the model.

Error-Correcting Output Codes Model

An error-correcting output codes (ECOC) model reduces the problem of classification with three or more classes to a set of binary classification problems.

ECOC classification requires a coding design, which determines the classes that the binary learners train on, and a decoding scheme, which determines how the results (predictions) of the binary classifiers are aggregated.

Assume the following:

• The classification problem has three classes.

• The coding design is one-versus-one. For three classes, this coding design is

  $$\begin{array}{cccc}& \text{Learner 1}& \text{Learner 2}& \text{Learner 3}\\ \text{Class 1}& 1& 1& 0\\ \text{Class 2}& -1& 0& 1\\ \text{Class 3}& 0& -1& -1\end{array}$$

  You can specify a different coding design by using the Coding name-value argument when you create a classification model.

• The model determines the predicted class by using the loss-weighted decoding scheme with the binary loss function g. The software also supports the loss-based decoding scheme. You can specify the decoding scheme and binary loss function by using the Decoding and BinaryLoss name-value arguments, respectively, when you create a classification model or when you call the object functions predict and loss.

To build this classification model, the ECOC algorithm follows these steps.

1. Learner 1 trains on observations in Class 1 or Class 2, and treats Class 1 as the positive class and Class 2 as the negative class. The other learners are trained similarly.

2. Let M be the coding design matrix with elements m_kl, and s_l be the predicted classification score for the positive class of learner l. The algorithm assigns a new observation to the class ($$\widehat{k}$$) that minimizes the aggregation of the losses for the L binary learners.

   $$\widehat{k}=\underset{k}{\text{argmin}}\frac{{\displaystyle \sum }_{l=1}^B\left|m_{kl}\right|g\left(m_{kl},s_l\right)}{{\displaystyle \sum }_{l=1}^B\left|m_{kl}\right|}.$$

ECOC models can improve classification accuracy, compared to other multiclass models [4].

Coding Design

The coding design is a matrix whose elements direct which classes are trained by each binary learner, that is, how the multiclass problem is reduced to a series of binary problems.

Each row of the coding design corresponds to a distinct class, and each column corresponds to a binary learner. In a ternary coding design, for a particular column (or binary learner):

• A row containing 1 directs the binary learner to group all observations in the corresponding class into a positive class.

• A row containing –1 directs the binary learner to group all observations in the corresponding class into a negative class.

• A row containing 0 directs the binary learner to ignore all observations in the corresponding class.

Coding design matrices with large, minimal, pairwise row distances based on the Hamming measure are optimal. For details on the pairwise row distance, see Random Coding Design Matrices and [3].

This table describes popular coding designs.

Coding Design	Description	Number of Learners	Minimal Pairwise Row Distance
one-versus-all (OVA)	For each binary learner, one class is positive and the rest are negative. This design exhausts all combinations of positive class assignments.	K	2
one-versus-one (OVO)	For each binary learner, one class is positive, one class is negative, and the rest are ignored. This design exhausts all combinations of class pair assignments.	K(K – 1)/2	1
binary complete	This design partitions the classes into all binary combinations, and does not ignore any classes. That is, all class assignments are –1 and 1 with at least one positive class and one negative class in the assignment for each binary learner.	2K – 1 – 1	2K – 2
ternary complete	This design partitions the classes into all ternary combinations. That is, all class assignments are 0, –1, and 1 with at least one positive class and one negative class in the assignment for each binary learner.	(3K – 2K + 1 + 1)/2	3K – 2
ordinal	For the first binary learner, the first class is negative and the rest are positive. For the second binary learner, the first two classes are negative and the rest are positive, and so on.	K – 1	1
dense random	For each binary learner, the software randomly assigns classes into positive or negative classes, with at least one of each type. For more details, see Random Coding Design Matrices.	Random, but approximately 10 log2K	Variable
sparse random	For each binary learner, the software randomly assigns classes as positive or negative with probability 0.25 for each, and ignores classes with probability 0.5. For more details, see Random Coding Design Matrices.	Random, but approximately 15 log2K	Variable

This plot compares the number of binary learners for the coding designs with an increasing number of classes (K).

Binary Loss

The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.

Assume the following:

• m_kj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.

• s_j is the score of binary learner j for an observation.

• g is the binary loss function.

• $$\widehat{k}$$ is the predicted class for the observation.

The software supports two decoding schemes:

• Loss-based decoding [3] (Decoding is "lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.

  $$\widehat{k}=\underset{k}{\text{argmin}}\frac{1}{B}{\displaystyle \sum _{j=1}^B\left|m_{kj}\right|g}(m_{kj},s_j).$$

• Loss-weighted decoding [2] (Decoding is "lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.

  $$\widehat{k}=\underset{k}{\text{argmin}}\frac{{\displaystyle \sum _{j=1}^B\left|m_{kj}\right|g}(m_{kj},s_j)}{{\displaystyle \sum }_{j=1}^B\left|m_{kj}\right|}.$$

  The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.

The predict, resubPredict, and kfoldPredict functions return the negated value of the objective function of argmin as the second output argument (NegLoss) for each observation and class.

This table summarizes the supported binary loss functions, where y_j is a class label for a particular binary learner (in the set {–1,1,0}), s_j is the score for observation j, and g(y_j,s_j) is the binary loss function.

Value	Description	Score Domain	g(yj,sj)
"binodeviance"	Binomial deviance	(–∞,∞)	log[1 + exp(–2yjsj)]/[2log(2)]
"exponential"	Exponential	(–∞,∞)	exp(–yjsj)/2
"hamming"	Hamming	[0,1] or (–∞,∞)	[1 – sign(yjsj)]/2
"hinge"	Hinge	(–∞,∞)	max(0,1 – yjsj)/2
"linear"	Linear	(–∞,∞)	(1 – yjsj)/2
"logit"	Logistic	(–∞,∞)	log[1 + exp(–yjsj)]/[2log(2)]
"quadratic"	Quadratic	[0,1]	[1 – yj(2sj – 1)]2/2

The software normalizes binary losses so that the loss is 0.5 when y_j = 0, and aggregates using the average of the binary learners [1].

Do not confuse the binary loss with the overall classification loss (specified by the LossFun name-value argument of the loss and predict object functions), which measures how well an ECOC classifier performs as a whole.

Classification Error

The classification error has the form

$$L={\displaystyle \sum _{j=1}^n{w}_j{e}_j},$$

where:

• w_j is the weight for observation j. The software renormalizes the weights to sum to 1.

• e_j = 1 if the predicted class of observation j differs from its true class, and 0 otherwise.

In other words, the classification error is the proportion of observations misclassified by the classifier.

Algorithms

Performance Metrics

• The updateMetrics and updateMetricsAndFit functions track model performance metrics (Metrics) from new data only when the incremental model is warm (IsWarm property is true).

  • If you create an incremental model by using incrementalLearner and MetricsWarmupPeriod is 0 (default for incrementalLearner), the model is warm at creation.

  • Otherwise, an incremental model becomes warm after fit or updateMetricsAndFit performs both of these actions:

    • Fit the incremental model to MetricsWarmupPeriod observations, which is the metrics warm-up period.

    • Fit the incremental model to all expected classes (see the MaxNumClasses and ClassNames arguments of incrementalClassificationECOC).

• The Metrics property of the incremental model stores two forms of each performance metric as variables (columns) of a table, Cumulative and Window, with individual metrics in rows. When the incremental model is warm, updateMetrics and updateMetricsAndFit update the metrics at the following frequencies:

  • Cumulative — The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.

  • Window — The functions compute metrics based on all observations within a window determined by MetricsWindowSize, which also determines the frequency at which the software updates Window metrics. For example, if MetricsWindowSize is 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:) and Y((end – 20 + 1):end)).

    Incremental functions that track performance metrics within a window use the following process:

    1. Store a buffer of length MetricsWindowSize for each specified metric, and store a buffer of observation weights.

    2. Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.

    3. When the buffer is full, overwrite the Window field of the Metrics property with the weighted average performance in the metrics window. If the buffer overfills when the function processes a batch of observations, the latest incoming MetricsWindowSize observations enter the buffer, and the earliest observations are removed from the buffer. For example, suppose MetricsWindowSize is 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.

• The software omits an observation with a NaN score when computing the Cumulative and Window performance metric values.

Custom Coding Design Matrices

Custom coding matrices must have a certain form. The software validates a custom coding matrix by ensuring:

• Every element is –1, 0, or 1.

• Every column contains as least one –1 and one 1.

• For all distinct column vectors u and v, u ≠ v and u ≠ –v.

• All row vectors are unique.

• The matrix can separate any two classes. That is, you can move from any row to any other row following these rules:

  • Move vertically from 1 to –1 or –1 to 1.

  • Move horizontally from a nonzero element to another nonzero element.

  • Use a column of the matrix for a vertical move only once.

  If it is not possible to move from row i to row j using these rules, then classes i and j cannot be separated by the design. For example, in the coding design

  $$\left[\begin{array}{cc}1& 0\\ -1& 0\\ 0& 1\\ 0& -1\end{array}\right]$$

  classes 1 and 2 cannot be separated from classes 3 and 4 (that is, you cannot move horizontally from –1 in row 2 to column 2 because that position contains a 0). Therefore, the software rejects this coding design.

Random Coding Design Matrices

For a given number of classes K, the software generates random coding design matrices as follows.

1. The software generates one of these matrices:

   1. Dense random — The software assigns 1 or –1 with equal probability to each element of the K-by-L_d coding design matrix, where $$L_d\approx \lceil 10{\log }_{2}K\rceil$$.

   2. Sparse random — The software assigns 1 to each element of the K-by-L_s coding design matrix with probability 0.25, –1 with probability 0.25, and 0 with probability 0.5, where $$L_s\approx \lceil 15{\log }_{2}K\rceil$$.

2. If a column does not contain at least one 1 and one –1, then the software removes that column.

3. For distinct columns u and v, if u = v or u = –v, then the software removes v from the coding design matrix.

The software randomly generates 10,000 matrices by default, and retains the matrix with the largest, minimal, pairwise row distance based on the Hamming measure ([3]) given by

$$\Delta (k_1,k_2)=0.5{\displaystyle \sum }_{l=1}^L\left|m_{k_{1}l}\right|\left|m_{k_{2}l}\right|\left|m_{k_{1}l}-m_{k_{2}l}\right|,$$

where m_kjl is an element of coding design matrix j.

References

[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.

[2] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.

[3] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.

[4] Fürnkranz, Johannes. “Round Robin Classification.” J. Mach. Learn. Res., Vol. 2, 2002, pp. 721–747.

[5] Kempka, Michał, Wojciech Kotłowski, and Manfred K. Warmuth. "Adaptive Scale-Invariant Online Algorithms for Learning Linear Models." Preprint, submitted February 10, 2019. https://arxiv.org/abs/1902.07528.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™. (since R2025a)

Usage notes and limitations:

• The fit, loss, predict, updateMetrics, and updateMetricsAndFit functions support code generation.

• When you create an incrementalClassificationECOC model object, the following restrictions apply.

  • You must specify ClassNames and NumPredictors.

  • The binary learners must be linear.

• When you generate code that loads or creates an incrementalClassificationECOC model object, the following restrictions apply.

  • The number of predictor variables must equal Mdl.NumPredictors.

  • The ClassNames property must contain all expected class names.

For more information, see Introduction to Code Generation.

Version History

Introduced in R2022a