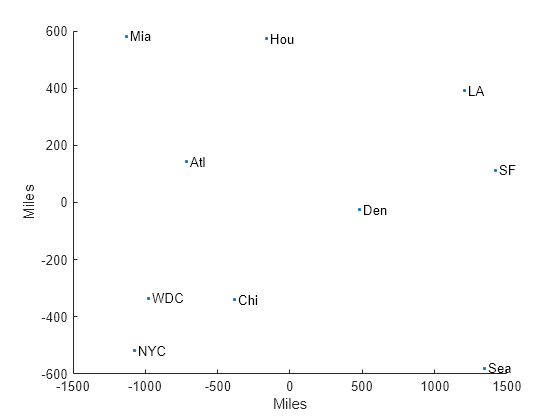
cmdscale
Classical multidimensional scaling
Description
Y = cmdscale(D)n-by-n
distance or dissimilarity matrix D, and returns an
n-by-p configuration matrix. The rows of
Y correspond to the coordinates of n points in a
p-dimensional space, where p <
n.
When D is a Euclidean distance matrix, its elements are the
pairwise distances between the n points, and p is the
dimension of the smallest space in which these points can be embedded.
When D is a non-Euclidean distance matrix or a dissimilarity
matrix, p is the number of positive eigenvalues of
Y*Y'. In this case, the reduction to p or fewer
dimensions provides a reasonable approximation to D only if the
negative eigenvalues of Y*Y' are small in magnitude.
Examples
Input Arguments
Output Arguments
References
[1] Cox, Trevor F., and Michael A. A. Cox. Multidimensional Scaling. 2nd ed. Monographs on Statistics and Applied Probability 88. Boca Raton: Chapman & Hall/CRC, 2001.
[2] Davison, Mark L. Multidimensional Scaling. Wiley Series in Probability and Mathematical Statistics. New York: Wiley, 1983.
[3] Seber, G. A. F. Multivariate Observations. 1st ed. Wiley Series in Probability and Statistics. Wiley, 1984.
Version History
Introduced before R2006a