N-Channel IGBT
N-Channel insulated gate bipolar transistor
Libraries:
Simscape /
Electrical /
Semiconductors & Converters
Description
The N-Channel IGBT block models an Insulated Gate Bipolar Transistor (IGBT). The block provides two main modeling options, by setting the Modeling option parameter to either:
Full I-V and capacitance characteristics — This modeling option is a detailed component model suitable for simulating detailed switching characteristics and predicting component losses. This modeling option, in turn, provides two ways of modeling an IGBT:
As an equivalent circuit based on a PNP bipolar transistor and N-channel MOSFET. For more information on using this model, see Representation by Equivalent Circuit, Fine-Tuning the Current-Voltage Characteristics, and Modeling Temperature Dependence.
By a 2-D lookup table approximation to the I-V (current-voltage) curve. For details, see Representation by 2-D Lookup Table.
By a 3-D lookup table approximation to the I-V (current-voltage) curve that includes temperature data. For details, see Representation by 3-D Lookup Table.
The gate capacitance in the detailed model is represented as a fixed gate-emitter capacitance CGE and either a fixed or a nonlinear gate-collector capacitance CGC. For details, see Charge Model.
Simplified I-V characteristics and event-based timing — This modeling option models the IGBT more simply by using just the on-state I-V data as a function of the collector-emitter voltage. In the off state (gate-emitter voltage less than Threshold voltage, Vth), the IGBT is modeled by a constant Off-state conductance. This simplified model is suitable when approximate dynamic characteristics are sufficient, and simulation speed is of paramount importance. For details, see Event-Based IGBT Modeling Option.
Together with the thermal port modeling options (see Thermal Port), the block therefore provides you with four choices. To select the desired modeling option, set the Modeling option parameter to either:
Full I-V and capacitance characteristics | No thermal port— Detailed model that does not simulate the effects of generated heat and device temperature. This is the default.Full I-V and capacitance characteristics | Show thermal port— Detailed model with exposed thermal port.Simplified I-V characteristics and event-based timing | No thermal port— Simplified event-based model, which also does not simulate the effects of generated heat and device temperature.Simplified I-V characteristics and event-based timing | Show thermal port— Simplified event-based model with exposed thermal port.
Representation by Equivalent Circuit
The equivalent circuit of the detailed block modeling option consists of a PNP Bipolar Transistor block driven by an N-Channel MOSFET block, as shown in the following figure:
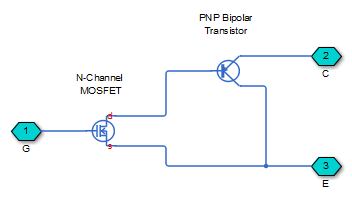
The MOSFET source is connected to the bipolar transistor collector, and the MOSFET drain is connected to the bipolar transistor base. The MOSFET uses the threshold-based equations shown in the N-Channel MOSFET block reference page. The bipolar transistor uses the equations shown in the PNP Bipolar Transistor block reference page, but with the addition of an emission coefficient parameter N that scales kT/q.
The N-Channel IGBT block uses the on and off characteristics you specify in the block dialog box to estimate the parameter values for the underlying N-Channel MOSFET and PNP bipolar transistor.
The block uses the off characteristics to calculate the base-emitter voltage, Vbe, and the saturation current, IS.
When the transistor is off, the gate-emitter voltage is zero and the IGBT base-collector voltage is large, so the PNP base and collector current equations simplify to:
where N is the Emission coefficient, N parameter value, VAF is the forward Early voltage, and Ic and Ib are defined as positive flowing into the collector and base, respectively. See the PNP Bipolar Transistor reference page for definitions of the remaining variables. The first equation can be solved for Vbe.
The base current is zero in the off-condition, and hence Ic = –Ices, where Ices is the Zero gate voltage collector current. The base-collector voltage, Vbc, is given by Vbc = Vces + Vces, where Vces is the voltage at which Ices is measured. Hence we can rewrite the second equation as follows:
The block sets βR and βF to typical values of 1 and 50, so these two equations can be used to solve for Vbe and IS:
Note
The block does not require an exact value for βF because it can adjust the MOSFET gain K to ensure the overall device gain is correct.
The block parameters Collector-emitter saturation voltage, Vce(sat) and Collector current at which Vce(sat) is defined are used to determine Vbe(sat) by solving the following equation:
Given this value, the block calculates the MOSFET gain, K, using the following equation:
where Vth is the Gate-emitter threshold voltage, Vge(th) parameter value, VGE(sat) is the Gate-emitter voltage at which Vce(sat) is defined parameter value, and TF is the Total forward transit time parameter value.
Vds is related to the transistor voltages as Vds = Vce – Vbe. The block substitutes this relationship for Vds, sets the base-emitter voltage and base current to their saturated values, and rearranges the MOSFET equation to give
where Vce(sat) is the Collector-emitter saturation voltage, Vce(sat) parameter value.
These calculations ensure the zero gate voltage collector current and collector-emitter saturation voltage are exactly met at these two specified conditions. However, the current-voltage plots are very sensitive to the emission coefficient N and the precise value of Vth. If the manufacturer datasheet gives current-voltage plots for different VGE values, then the N and Vth can be tuned by hand to improve the match.
Representation by 2-D Lookup Table
For the lookup table representation of the detailed block modeling option, you provide tabulated values for collector current as a function of gate-emitter voltage and collector-emitter voltage. The main advantage of using this option is simulation speed. It also lets you parameterize the device from either measured data or from data obtained from another simulation environment. To generate your own data from the equivalent circuit representation, you can use a test harness, such as shown in the IGBT Characteristics example.
The lookup table representation combines all of the equivalent circuit components (PNP transistor, N-channel MOSFET, collector resistor and emitter resistor) into one equivalent lookup table.
Note
To ensure that the signs of the collector-emitter current and collector-emitter voltage are consistent:
If the collector-emitter voltage is equal to
0, the value of the Tabulated collector currents, Ic(Vge,Vce) parameter must be equal to0.The tabulated power, which is the product of the Tabulated collector currents, Ic(Vge,Vce) parameter and the collector-emitter voltage, must be greater than or equal to
0.The tabulated conductance, which is the gradient of the Tabulated collector currents, Ic(Vge,Vce) parameter with respect to the collector-emitter voltage Vce, must be greater than or equal to
0.The first gradient of the Tabulated collector currents, Ic(Vge,Vce) parameter, with respect to gate-emitter voltage Vge, must be equal to
0.
Representation by 3-D Lookup Table
For the temperature-dependent lookup table representation of the detailed block modeling option, you provide tabulated values for collector current as a function of gate-emitter voltage, collector-emitter voltage, and temperature.
The lookup table representation combines all of the equivalent circuit components (PNP transistor, N-channel MOSFET, collector resistor and emitter resistor) into one equivalent lookup table.
If the block thermal port is not exposed, then the Device simulation temperature parameter on the Temperature Dependence setting lets you specify the simulation temperature.
Note
To ensure that the signs of the collector-emitter current and collector-emitter voltage are consistent:
If the collector-emitter voltage is equal to
0, the value of the Tabulated collector currents, Ic(Vge,Vce,T) parameter must be equal to0.The tabulated power, which is the product of the Tabulated collector currents, Ic(Vge,Vce,T) parameter and the collector-emitter voltage, must be greater than or equal to
0.The tabulated conductance, which is the gradient of the Tabulated collector currents, Ic(Vge,Vce,T) parameter with respect to the collector-emitter voltage Vce, must be greater than or equal to
0.The first gradient of the Tabulated collector currents, Ic(Vge,Vce,T) parameter, with respect to gate-emitter voltage Vge, must be equal to
0.
Charge Model
The detailed modeling option of the block models capacitances either by fixed capacitance values, or by tabulated values as a function of the collector-emitter voltage. In either case, you can either directly specify the gate-emitter and gate-collector capacitance values, or let the block derive them from the input and reverse transfer capacitance values. Therefore, the Parameterization options for charge model on the Junction Capacitance setting are:
Specify fixed input, reverse transfer and output capacitance— Provide fixed parameter values from datasheet and let the block convert the input and reverse transfer capacitance values to capacitance values, as described below. This is the default method.Specify fixed gate-emitter, gate-collector and collector-emitter capacitance— Provide fixed values for capacitance parameters directly.Specify tabulated input, reverse transfer and output capacitance— Provide tabulated capacitance and collector-emitter voltage values based on datasheet plots. The block converts the input and reverse transfer capacitance values to capacitance values, as described below.Specify tabulated gate-emitter, gate-collector and collector-emitter capacitance— Provide tabulated values for capacitances and collector-emitter voltage.
Use one of the tabulated capacitance options (Specify tabulated
input, reverse transfer and output capacitance or
Specify tabulated gate-emitter, gate-collector and
collector-emitter capacitance) when the datasheet provides a plot
of capacitances as a function of collector-emitter voltage. Using tabulated
capacitance values will give more accurate dynamic characteristics, and avoids the
need to iteratively tune parameters to fit the dynamics.
If you use the Specify fixed gate-emitter, gate-collector and
collector-emitter capacitance or Specify tabulated
gate-emitter, gate-collector and collector-emitter capacitance
option, the Junction Capacitance setting lets you specify the
Gate-emitter capacitance, Gate-collector
capacitance, and Collector-emitter capacitance
parameter values (fixed or tabulated) directly. Otherwise, the block derives them
from the Input capacitance, Cies, Reverse transfer
capacitance, Cres, and Output capacitance, Coes
parameter values. These two parameterization methods are related as follows:
CGC = Cres
CGE = Cies – Cres
CCE = Coes – Cres
The two fixed capacitance options (Specify fixed input, reverse
transfer and output capacitance or Specify fixed
gate-emitter, gate-collector and collector-emitter capacitance)
let you model gate capacitance as a fixed gate-emitter capacitance
CGE and either a fixed or a nonlinear
gate-collector capacitance CGC. If you
select the Gate-collector charge function is nonlinear
option for the Charge-voltage linearity parameter, then the
gate-collector charge relationship is defined by the piecewise-linear function shown
in the following figure.
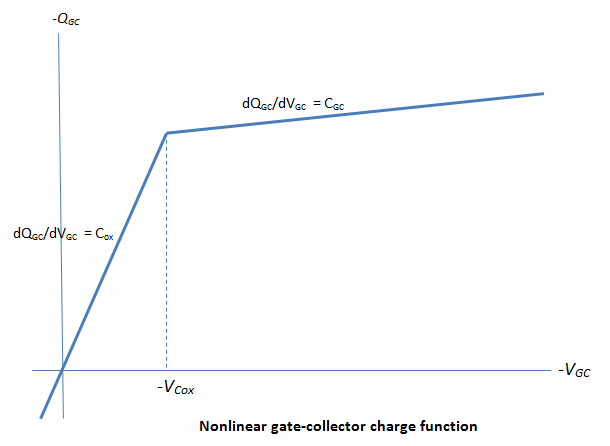
With this nonlinear capacitance, the gate-emitter and collector-emitter voltage profiles take the form shown in the next figure, where the collector-emitter voltage fall has two regions (labeled 2 and 3) and the gate-emitter voltage has two time-constants (before and after the threshold voltage Vth):
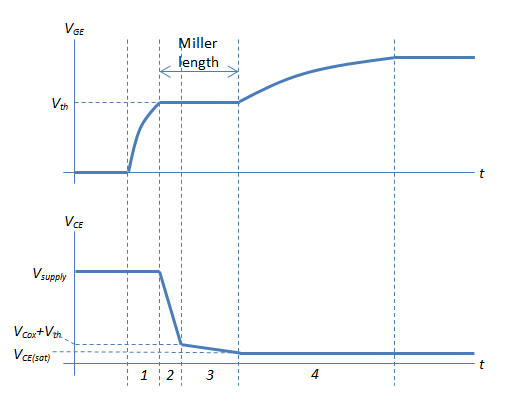
You can determine the capacitor values for Cies, Cres, and Cox as follows, assuming that the IGBT gate is driven through an external resistance RG:
Set Cies to get correct time-constant for VGE in Region 1. The time constant is defined by the product of Cies and RG. Alternatively, you can use a datasheet value for Cies.
Set Cres so as to achieve the correct VCE gradient in Region 2. The gradient is given by (VGE – Vth)/(Cres · RG).
Set VCox to the voltage at which the VCE gradient changes minus the threshold voltage Vth.
Set Cox to get correct Miller length and time constant in Region 4.
Because the underlying model is a simplification of an actual charge distribution, some iteration of these four steps may be required to get a best overall fit to measured data.
The collector current tail when the IGBT is turned off is determined by the
Total forward transit time parameter if you set the
I-V characteristics defined by parameter to
Fundamental nonlinear equation.
If you set the I-V characteristics defined by parameter to
Lookup table (2D, temperature independent) or
Lookup table (3D, temperature dependent), then the
collector current tail when the IGBT is turned off is determined by the
Turn-off tail current transit time parameter:
Where ioff is the IGBT turn-off current, ion is the IGBT turn-on current, toff is the turn-off time, and TT is the value of the Turn-off tail current transit time parameter.
Note
Because this block implementation includes a charge model, you must model the impedance of the circuit driving the gate to obtain representative turn-on and turn-off dynamics. Therefore, if you are simplifying the gate drive circuit by representing it as a controlled voltage source, you must include a suitable series resistor between the voltage source and the gate.
Fine-Tuning the Current-Voltage Characteristics
For the equivalent circuit representation of the detailed model, use the parameters on the Advanced setting to fine-tune the current-voltage characteristics of the modeled device. To use these additional parameters effectively, you will need a manufacturer datasheet that provides plots of the collector current versus collector-emitter voltage for different values of gate-emitter voltage. The parameters on the Advanced setting have the following effects:
The Emission coefficient, N parameter controls the shape of the current-voltage curves around the origin.
The Collector resistance, RC and Emitter resistance, RE parameters affect the slope of the current-voltage curve at higher currents, and when fully turned on by a high gate-emitter voltage.
The Forward Early voltage, VAF parameter affects the shape of the current-voltage curves for gate-emitter voltages around the Gate-emitter threshold voltage, Vge(th).
Modeling Temperature Dependence
For the 2-D lookup table representation, the electrical equations do not depend on temperature. However, you can model temperature dependence by either using the 3-D lookup table representation, or by using the equivalent circuit representation of the detailed model.
For the equivalent circuit representation, temperature dependence is modeled by the temperature dependence of the constituent components. See the N-Channel MOSFET and PNP Bipolar Transistor block reference pages for further information on the defining equations.
Some datasheets do not provide information on the zero gate voltage collector
current, Ices, at a higher measurement temperature. In this case,
you can alternatively specify the energy gap, EG, for the device,
using a typical value for the semiconductor type. For silicon, the energy gap is
usually 1.11 eV.
Event-Based IGBT Modeling Option
This implementation has much simpler equations than that with full I-V and capacitance characteristics. Use the event-based modeling option when the focus of the analysis is to understand overall circuit behavior rather than to verify the precise IGBT timing or losses characteristics.
The device is always in one of the following four states:
Off
Turning on
On
Turning off
In the off state, the relationship between collector current (ic) and collector-emitter voltage (vce) is
| ic = Goffvce | (1) |
In the on state, the relationship between collector current (ic) and collector-emitter voltage (vce) is
| vce = tablelookup(ic) | (2) |
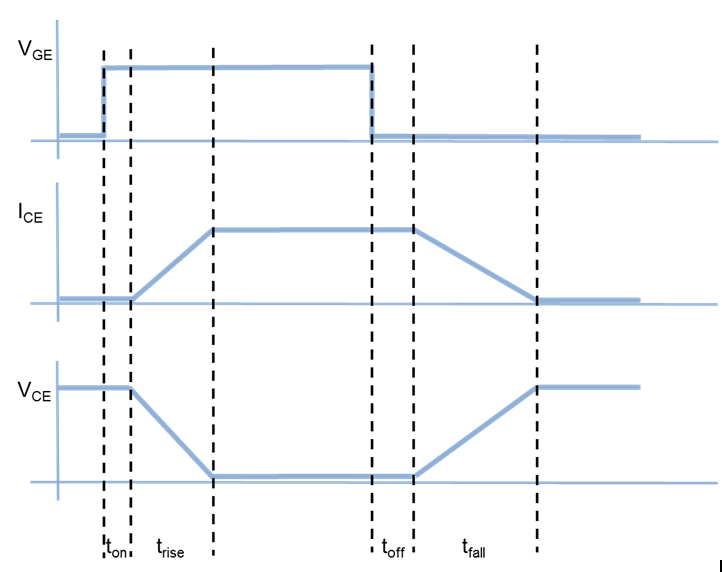
When turning on, the collector-emitter voltage is ramped down to zero over the rise time, the device moving into the on state when the voltage falls below the tabulated on-state value. Similarly when turning off, the collector-emitter voltage is ramped up over the (current) fall time to the specified blocking voltage value.
The following figure shows the resulting voltage and current profiles when driving a resistive load.
Thermal Port
The block has an optional thermal port, hidden by default. To expose the thermal port, set the Modeling option parameter to:
Full I-V and capacitance characteristics | Show thermal port— Detailed model. This action displays the thermal port H on the block icon, and exposes the Thermal Port parameters.Simplified I-V characteristics and event-based timing | Show thermal port— Simplified event-based model. This action displays the thermal port H on the block icon, exposes Thermal Port parameters and additional Main parameters. To simulate thermal effects, you must provide additional tabulated data for turn-on and turn-off losses and define the collector-emitter on-state voltage as a function of both current and temperature.
Use the thermal port to simulate the effects of generated heat and device temperature. For more information on using thermal ports and on the Thermal Port parameters, see Simulating Thermal Effects in Semiconductors.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
This table shows the relationship between the capacitances of the block and the initial targets:
| Defined Capacitance | Initial Targets |
|---|---|
| Gate-emitter capacitance, Cge | Set the initial target for the gate-emitter capacitance voltage only. Set the initial target of the collector-emitter capacitance voltage to 0 or set its priority to None. |
| Collector-emitter capacitance, Cce | Set the initial target for the collector-emitter capacitance voltage only. Set the initial target of the gate-emitter capacitance voltage to 0 or set its priority to None. |
| Gate-collector capacitance, Cgc | Set the initial targets for the gate-collector voltages by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and collector-emitter. |
| Gate-emitter capacitance, Cge, and gate-collector capacitance, Cgc | Set the initial targets for the gate-emitter and gate-collector voltages by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and the collector-emitter. |
| Gate-emitter capacitance, Cge, and collector-emitter capacitance, Cce | Set the initial target for the gate-emitter and the collector-emitter capacitance. |
| Gate-collector capacitance, Cgc, and collector-emitter capacitance, Cce | Set the initial targets for the gate-collector and collector-emitter voltages by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and the collector-emitter. |
| Gate-emitter capacitance, Cge, gate-collector capacitance, Cgc, and collector-emitter capacitance, Cce | Set the initial targets for the gate-emitter, gate collector and collector-emitter capacitances by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and the collector-emitter. |
Note
Inside your model, the number of initial targets with Priority equal to Low or High must match the number of differential variables. The differential variables come from the inductors and the capacitances in the model.
Plot Basic I-V Characteristics
You can plot the basic I-V characteristics of the N-Channel IGBT block without building a complete model. Use the plots to explore the impact of your parameter choices on device characteristics. If you parameterize the block from a data sheet, you can compare your plots to the data sheet to check that you parameterized the block correctly. If you have a complete working model but do not know which manufactured part to use, you can compare your plots to data sheets to help you decide.
To enable this option, set the Modeling option parameter of
the N-Channel IGBT block to Full I-V and capacitance characteristics | No
thermal port. To plot the basic characteristics, right-click the
block and select Electrical > Basic
characteristics from the context menu. For more information about
the Basic characteristics option, see Plot Basic I-V Characteristics of Semiconductor Blocks.
Examples
Assumptions and Limitations
The detailed model is based on the following assumptions:
This block does not allow you to specify initial conditions on the capacitances. If you select the Start simulation from steady state option in the Solver Configuration block, the block solves the initial voltages to be consistent with the calculated steady state. Otherwise, voltages are zero at the start of the simulation.
You may need to use nonzero capacitance values to prevent numerical simulation issues, but the simulation may run faster with these values set to zero.
The block does not account for temperature-dependent effects on the capacitances.
The simplified, event-based model is based on the following assumptions:
When you use a pair of IGBTs in a bridge arm, normally the gate drive circuitry will prevent a device turning on until the corresponding device has turned off, thereby implementing a minimum dead band. If you need to simulate the case where there is no minimum dead band and both devices are momentarily partially on, use the detailed IGBT model modeling option (Full I-V and capacitance characteristics). The assumption used by the event-based modeling option that the collector-emitter voltages can be ramped between on and off states is not valid for such cases.
A minimum pulse width is applied when turning on or off; at the point where the gate-collector voltage rises above the threshold, any subsequent gate voltage changes are ignored for a time equal to the sum of the turn-on delay and current rise time. Similarly at the point where the gate collector voltage falls below the threshold, any subsequent gate voltage changes are ignored for a time equal to the sum of the turn-off delay and current fall time. This feature is normally implemented in the gate drive circuitry.
This model does not account for charge. Hence there is no current tail when turning off an inductive load.
Representative modeling of the current spike during turn-on of an inductive load with preexisting freewheeling current requires tuning of the Miller resistance parameter.
The tabulated turn-on switching loss uses the previous on-state current, not the current value (which is not known until the device reaches the final on state).
Due to high model stiffness that can arise from the simplified equations, you may get minimum step size violation warnings when using this block. Open the Solver pane of the Configuration Parameters dialog box and increase the Number of consecutive min steps parameter value as necessary to remove these warnings.
Due to how the block calculates the collector-emitter voltage, if you want to model multiple N-Channel IGBT blocks in parallel, use a single N-Channel IGBT block and multiply the value of the Vector of collector currents, Ic parameter by the number of IGBT devices that you wanted to model in parallel.





