Change Operating Point Search Optimization Settings

When trimming a Simulink^® model, you can control the accuracy of your operating point search by configuring the optimization algorithm. Typically, you adjust the optimization settings based on the operating point search report, which is automatically created after each search.

You can change your optimization settings when computing operating points interactively using the Steady State Manager or Model Linearizer, or programmatically using the findop function.

For more information on computing operating points from specifications, see Compute Steady-State Operating Points from Specifications.

Programmatically Change Optimization Settings

To configure the optimization settings for computing operating points using the findop function, create a findopOptions object. For example, create an options object and specify a nonlinear least-squares optimization method.

options = findopOptions('OptimizerType','lsqnonlin');

To specify options for each optimization method, set the OptimizationOptions parameter of the options object to a corresponding structure created using the optimset (Optimization Toolbox) function.

To specify custom cost and constraint functions for optimization, create an operspec object and specify the CustomObjFcn, CustomConstrFcn, and CustomMappingFcn properties. For more information, see Compute Operating Points Using Custom Constraints and Objective Functions.

Interactively Change Optimization Settings

You can configure the optimization settings for interactively computing operating points using Steady State Manager or Model Linearizer using the same trimming options dialog box interface.

In Steady State Manager, on the Specification tab, click Trim Options. Then, in the Trim Options dialog box, specify your optimization settings.
In Model Linearizer, on the Linear Analysis tab, in the Operating Point drop-down list, click Trim Model. Then, in the Trim the model dialog box, on the Options tab, specify your optimization settings.

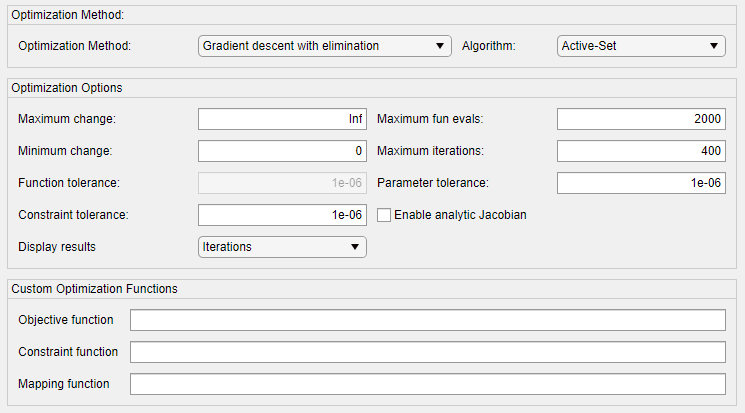
To configure the options for your operating point search:

Choose the optimization method and algorithm in the Optimization Method section. For more information, see Specify Optimization Method.
Specify options for the chosen optimization method in the Optimization Options section. These options include tolerances and stopping conditions for the search algorithm. For more information, see Configure Optimization Options.
You can also specify custom cost and constraint functions for optimization in the Custom Optimization Functions section. For more information, see Define Custom Optimization Functions.

Specify Optimization Method

When you provide partial information or specifications for an operating point, the software uses an optimization method to search for operating point values. You can select an optimization method from one of the following classes. methods:

Gradient descent
Simplex search
Nonlinear least squares

For more information on choosing an optimization solver, see Choosing the Algorithm (Optimization Toolbox).

Gradient Descent

The gradient descent optimization method is based on the fmincon (Optimization Toolbox) function. All three gradient descent algorithms enforce constraints on output signals (y) and an equality constraint to force time derivatives of states to be zero: dx/dt = 0, x(k+1) = x(k).

Gradient descent — Minimizes the error between the operating point values the known values of states (x), inputs (u), and outputs (y). If there are no constraints on x, u, or y, the operating point search attempts to minimize the deviation between the initial guesses for x and u and the trimmed values.
Gradient descent with elimination — Like the Gradient descent algorithm, but it also fixes the known states and inputs by not allowing these variables to be optimized.
Gradient descent with projection — Like the Gradient descent algorithm, but forces the consistency of the model initial conditions at each evaluation of the objective and constraint functions, which can improve trimming results for Simscape™ models. This method requires Optimization Toolbox™ software.

For all three gradient descent methods, you can use one of the following algorithms.

Active-Set — Transforms active inequality constraints into simpler equality constraints and solves the simpler equality-constrained subproblem. This algorithm is the default setting and can be used in most cases.
Interior-Point — Optimizes by solving a sequence of approximate minimization problems. This algorithm can yield better performance for models with a very large number of states.
Trust-Region-Reflective — Optimizes by approximating the cost function by a simpler function within a region of a current point. This algorithm can yield better performance for models with a very large number of states.
Sequential Quadratic Programming (SQP) — Optimizes by solving a sequence of optimization subproblems, each of which optimizes a quadratic model of the objective subject to a linearization of the constraints

For more information on these algorithms, see Constrained Nonlinear Optimization Algorithms (Optimization Toolbox).

Simplex Search

The Simplex search method fixes the known states (x) and inputs (u) by not allowing these variables to be optimized. The algorithm then uses the fminsearch function to minimize the error in the state derivatives (dx/dt = 0) and the outputs (y).

Nonlinear Least Squares

The Nonlinear least squares method fixes the known states (x) and inputs (u) by not allowing these variables to be optimized. The algorithm then uses the lsqnonlin (Optimization Toolbox) function to minimize the error in the state derivatives (dx/dt = 0) and outputs (y). This optimization method often works well computing operating points that include states with algebraic relationships, as in Simscape Multibody™ models.

The Nonlinear least squares with projection method additionally enforces the consistency of the model initial conditions at each evaluation of the objective and constraint functions, which can improve trimming results for Simscape models. This method requires Optimization Toolbox software.

For both nonlinear least squares optimization methods, the algorithm choices are:

Levenberg-Marquardt — This algorithm is the default setting and can be used in most cases. For more information about this algorithm, see Levenberg-Marquardt Method (Optimization Toolbox).
Trust-Region-Reflective — Optimizes by approximating the cost function by a simpler function within a region of a current point. This algorithm can yield better performance for models with a very large number of states. For more information about this algorithm, see Trust-Region-Reflective Least Squares Algorithm (Optimization Toolbox).

Configure Optimization Options

You can configure your operating point search using the options in the following table.

Option	Behavior
Maximum change — Specify maximum absolute change of state or input values in finite difference gradient calculations	Increasing Maximum change allows the optimization to take larger steps during the optimization, which can help the optimization converge or leave a local minimum. Decreasing Maximum change limits the step size that the optimization routine can take, which can help find a more accurate solution when the system is smooth. By adjusting Maximum change and Minimum change appropriately, you can encourage the optimization to pass over regions of discontinuity. This option is not supported for the `Simplex search` optimization method
Minimum change — Specify minimum absolute change of state or input values in finite difference gradient calculations	Increasing Minimum change forces the optimization to take steps above a certain size, which can help the optimization converge or leave a local minimum. Decreasing Minimum change allows the optimization to take smaller steps, which can help find a more accurate solution when the system is smooth. By adjusting Minimum change and Maximum change appropriately, you can encourage the optimization to pass over regions of discontinuity. This option is not supported for the `Simplex search` optimization method
Function tolerance — Specify termination tolerance on function value	When function values on successive iterations are less than the Function tolerance, the optimization terminates. Decreasing Function tolerance forces the optimization to search for a solution when successive cost function values are closer together, which is likely to produce a more accurate solution with slower convergence. Increasing Function tolerance allows the optimization to terminate when successive cost function values are further apart, which is likely to produce a less accurate solution with faster convergence. This option is not supported for the `Gradient descent with elimination` optimization method
Constraint tolerance — Specify termination tolerance on equality constraint function	When the equality constraint function values on successive iterations are less than the Constraint tolerance, the optimization terminates. Decreasing Constraint tolerance forces the optimization to search for a solution when successive constraint function values are closer together, which is likely to produce a more accurate solution with slower convergence. Increasing Constraint tolerance allows the optimization to terminate when successive constraint function values are further apart, which is likely to produce a less accurate solution with faster convergence. This option is not supported for the following: `Simplex search` optimization method `Nonlinear least squares` optimization method `Nonlinear least squares with projection` optimization method
Maximum fun evals — Specify maximum number of cost function evaluations before optimization terminates	Increasing Maximum fun evals increases the computation time when searching for a solution. Decreasing Maximum fun evals decreases the computation time when searching for a solution. Tip There are potentially several evaluations of the cost function at each iteration. As a result, changing the Maximum iterations field can also affect the computation time.
Maximum iterations — Specify maximum number of iterations before optimization terminates	Increasing Maximum iterations allows the optimization to spend more time computing a solution. Decreasing Maximum iterations forces the optimization to terminate its computation earlier. Tip Each iteration potentially includes several cost function evaluations. As a result, changing the Maximum fcn evals field can also affect the computation time.
Parameter tolerance — Specify termination tolerance on state and input values	When the maximum change in the state and input values changes by less than the Parameter tolerance between successive iterations, the optimization terminates. Decreasing Parameter tolerance forces the optimization to search for a solution where state and input values on subsequent iterations are closer together, which is likely to produce a more accurate solution with slower convergence. Increasing Parameter tolerance allows the optimization to terminate when subsequent state and input values are further apart, which is likely to produce a less accurate solution with faster convergence.
Enable analytic Jacobian — Specify method for computing Jacobian during trimming	At each iteration, the operating point search algorithm computes the Jacobian of the system by linearizing about the current operating point. When you select the Enable analytic Jacobian option, the operating point search computes the Jacobian at each iteration by linearizing the model about the current operating point. When possible, it uses the preprogrammed, analytic linearizations for each block and when this is not possible, it numerically perturbs each block. When you clear this option, the operating point search computes the Jacobian by numerically perturbing the entire model. This option is not supported for the following: `Simplex search` optimization method `Gradient descent with projection` optimization method `Nonlinear least squares with projection` optimization method Models that use a Model block to include references to other models. Simscape Multibody models that are in `Trimming` mode.
Display results — Specify optimization progress to display	`Iterations` — Display the results of each iteration in the Trim Progress Viewer window. The displayed results include the maximum block error at each iteration and the block contributing to this error. `On` — Display the final optimization results in the MATLAB^® command window. `Off` — Do not display results.

Define Custom Optimization Functions

Some systems or applications require additional flexibility in defining the optimization search parameters, which you can provide by defining custom constraints, an additional objective function, or both.

To do so, you can define custom functions in the current working folder or on the MATLAB path. Then, in the corresponding custom function field, specify the function name.

Objective function — When the software computes a steady-state operating point, it applies your custom objective function in addition to the standard state, input, and output specifications.
Constraint function — When the software computes a steady-state operating point, it applies your custom constraints in addition to the standard state, input, and output specifications.
Mapping function — When specifying custom constraints and objective functions for trimming complex models, you can simplify the custom functions by eliminating unneeded states, inputs, and outputs. To do so, create a custom mapping function.

If your custom objective or constraint function returns an analytic gradient, you must select the Enable analytic Jacobian option.

For more information, see Compute Operating Points Using Custom Constraints and Objective Functions.