Analyze Impact of Model Parameters on Bouncing Ball Simulation

This example analyzes the impact of the damping coefficient on a mass-spring-damper model of the dynamics of a bouncing ball. After running a simulation using a vectorized parameter value, the example analyzes the effect of varying the parameter by exploring these questions:

• What is the effect on the position of the ball throughout the simulation?

• How do the states of the system change throughout the simulation?

• Does the damping affect the number of times the ball bounces?

• Does the damping affect the timing of the bounces?

By modifying parameter values, you can simulate multiple designs, tune and optimize parameter values, and simulate the behavior of the model under different conditions. The effect a parameter has on the simulation depends on how the parameter relates to the system equations that govern the behavior of the model. Some parameters can have a significant effect on simulation results, performance, or stability. Parameter impact analysis through simulation can help you understand systems and models and support efficient and effective Model-Based Design.

Mass-Spring-Damper Model of Bouncing Ball

To model the dynamics of a bouncing ball, consider the forces that act on the ball.

• When the ball is in the air, only the force due to gravity acts on the ball.

• When the ball is in contact with the surface, both the force due to gravity and the force from the collision with the surface act on the ball.

The difference in the system dynamics based on the position of the ball makes the bouncing ball an example of a hybrid dynamic system. Hybrid dynamic systems have both continuous dynamics and discrete transitions at which the system dynamics change and the system state values can "jump" or have discontinuities. In the model of the bouncing ball, the discrete transitions occur when the ball makes contact with the surface on which it bounces and when the ball bounces off of the surface into the air.

These equations represent the dynamics of the bouncing ball when the ball is in the air:

$$\frac{\mathrm{dv}}{\mathrm{dt}}=-\mathit{g}$$

$$\frac{\mathrm{dx}}{\mathrm{dt}}=\mathit{v},$$

where $\mathit{g}$ is the acceleration due to gravity, $\mathit{v}$ is the velocity of the ball, and $\mathit{x}$ is the position of the ball.

The example Simulation of Bouncing Ball models the interaction of the ball with the surface on which it bounces using a single parameter, the coefficient of restitution. The coefficient of restitution represents the energy loss and restoring force of each bounce. This example models the collision of the ball with the surface as a mass-spring-damper system with nonlinearity.

The mass-spring-damper approach models the interaction of the ball and surface with higher fidelity, incorporating compression and deformation that occurs during the collision. With this approach, the position of the ball can become negative as a result of the ball compressing and the surface bending or compressing on impact.

This second-order differential equation represents the dynamics of the bouncing ball when the ball is in contact with the surface using a mass-spring-damper approach:

$$\mathit{m}\ddot{\mathit{x}}+\mathit{c}\dot{\mathit{x}}+\mathrm{kx}+\alpha {\mathit{x}}^3=-\mathrm{mg},$$

where:

• $\dot{\mathit{x}}$ is the first derivative of the position, which corresponds to the velocity of the ball

• $\ddot{\mathit{x}}$ is the second derivative of the position, which corresponds to the acceleration of the ball

• $\mathit{g}$ is the acceleration due to gravity

• $\mathit{m}$ is the mass of the ball

• $\mathit{k}$ represents the linear stiffness of the ball and the surface on which it bounces

• $\mathit{c}$ represents damping in the interaction between the ball and the surface

• $\alpha$ represents nonlinearity in the restoring force

You can also represent the system using two first-order equations:

$$\frac{\mathrm{dv}}{\mathrm{dt}}=-\mathit{g}-\frac{\mathit{c}}{\mathit{m}}\mathit{v}-\frac{\mathit{k}}{\mathit{m}}\mathit{x}-\frac{\alpha }{\mathit{m}}{\mathit{x}}^3$$

$$\frac{\mathrm{dx}}{\mathrm{dt}}=\mathit{v}.$$

When $\alpha =0$, the equation becomes linear, leaving only the linear damping and stiffness coefficients $\mathit{c}$ and $\mathit{k}$. This example analyzes the impact of the damping coefficient $\mathit{c}$.

Open Simulink Model

Open the model ModelParameterImpact, which implements the mass-spring-damper model of the bouncing ball using Simulink®.

mdl = "ModelParameterImpact";
open_system(mdl)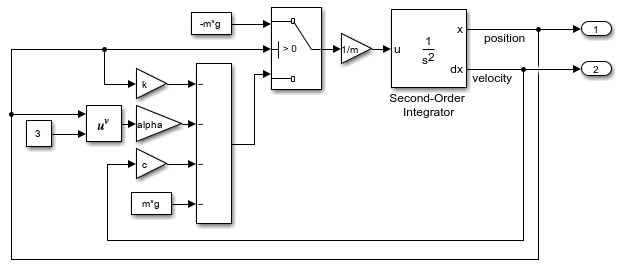

A Switch block models the discrete transition in the bouncing ball dynamics based on the position of the ball.

• When the position of the ball is greater than 0, only gravity contributes to the acceleration of the ball.

• When the position of the ball is less than or equal to zero, gravity, the mass-spring-damper terms, and the nonlinear term contribute to the acceleration of the ball.

The Second-Order Integrator block computes the position and velocity of the ball, and two Outport blocks create output ports for the position and velocity signals. Constant blocks, Gain blocks, and mathematical function blocks implement the other terms in the system equations. To parameterize the model, the Value parameters of the Constant blocks, the Gain parameters of the Gain blocks, and the initial state parameters of the Second-Order Integrator block are defined using variables. Because the Output model configuration parameter is enabled by default, the Outport blocks log the position and velocity signals during simulation.

Simulate Several Parameter Values

This example runs a single simulation using a vectorized parameter to generate results for several values of the damping coefficient. Rather than simulating several variations of a single bouncing ball, this approach simulates several different bouncing balls at once.

• While parameter vectorization works well to vary a single parameter, the approach does not scale to multiple parameters or Monte Carlo analysis. For information about scalable parameter sweeping and tuning workflows, see Configure and Run Simulations with Multiple Simulations Panel. For an example, see Use Multiple Simulations Panel to Run Design Study with Different Parameter Values.

• Parameter vectorization is not equivalent to running simulations in parallel. To run parallel simulations, use the parsim function.

To set the parameter values in the model, define the variables in the workspace. The table summarizes the parameter values used in this example.

Variable Name	Parameter Value	Units	Description
g	9.81	$\frac{\mathit{m}}{{\mathit{s}}^2}$	Acceleration due to gravity
k	2000	$\frac{\mathit{N}}{\mathit{m}}$	Stiffness of the surface and ball
alpha	2	$\frac{\mathit{N}}{{\mathit{m}}^3}$	Nonlinearity in restoring force
m	1	$$\mathrm{kg}$$	Mass of each ball
c	[0 15 25 50 100]	$\frac{\mathrm{Ns}}{\mathit{m}}$	Vector of damping coefficient values for five different balls
x0	20	$\mathit{m}$	Initial position of each ball
v0	0	$\frac{\mathit{m}}{\mathit{s}}$	Initial velocity of each ball

g = 9.81;
k = 2000;
alpha = 2;
m = 1;
c = [0 15 25 50 100];
x0 = 20;
v0 = 0;

Simulate the model.

out = sim(mdl);

Plot Position of Bouncing Balls

To see the results, plot the position of the five bouncing balls from the simulation.

pos = getElement(out.result,"position").Values;

plot(pos,LineWidth=1.5)
grid on
title("Bouncing Balls with Different Damping Coefficients")
ylabel("Position (m)")
legendvals = arrayfun(@(x) sprintf("c = %d", x),c,UniformOutput=false);
legend(legendvals,Location="best",Orientation="horizontal")

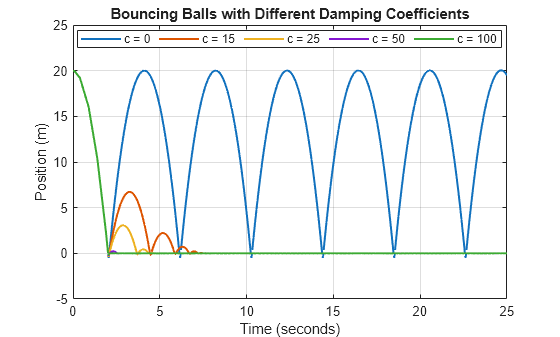
The results match expectations for varying the amount of damping in the system.

• When $\mathit{c}$ is 0, the results indicate the system has no damping: the ball bounces continually, returning to the same height with each bounce.

• As the value of $\mathit{c}$ increases, the ball bounces and then comes to rest, and the height of each successive bounce decays more steeply.

• When $\mathit{c}$ is 100, the system is overdamped: the ball comes to rest after the first collision and does not bounce.

Create Phase Portrait to Visualize System States

To analyze a dynamic system, you can create a phase portrait. The phase portrait visualizes the way the states in the system vary together over time in the phase space, also known as the state space. By viewing the phase portrait of a system, you can easily analyze the stability of the system, identify equilibrium points that indicate steady-state operation, and observe dynamic behaviors such as limit cycles.

The second-order model of the bouncing ball has two states: the position and the velocity of the ball. Create a phase portrait of the states in the bouncing ball model by plotting the position on the $\mathit{x}$-axis and the velocity on the $\mathit{y}$-axis. Use the quiver function to annotate the trajectory of each ball with an arrow that represents the direction in which the states evolve over time.

vel = getElement(out.result,"velocity").Values;

scalefactor = [1 2 2.5 3 5];
lastidx = size(pos.Data,1);
idx = 30;
startx = (pos.Data(idx,:) - pos.Data(idx-1,:)).*scalefactor;
starty = (vel.Data(idx,:) - vel.Data(idx-1,:)).*scalefactor;

plot(pos.Data,vel.Data,LineWidth=1)
grid on
hold on
quiver(pos.Data(idx,:),vel.Data(idx,:),startx,starty,0,'k');
title("Bouncing Balls with Different Damping Coefficients")
xlabel("Position (m)")
ylabel("Velocity (m/s)")
legend(legendvals)
hold off

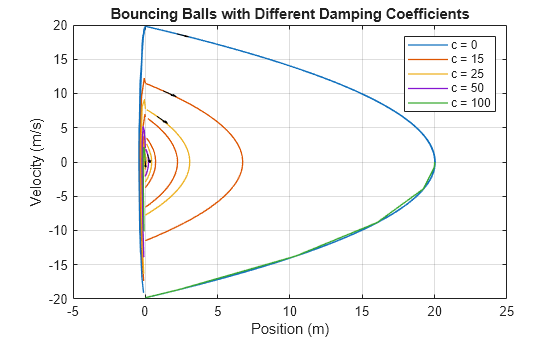
The phase portrait shows a closed limit cycle for the undamped bouncing ball. The trajectories of the bouncing balls that have nonzero damping start from the initial position and velocity and spiral inward to an equilibrium point at which the ball is at rest on the surface, with both a position and velocity of 0.

Postprocess Simulation Output

To further analyze the effect of the damping coefficient on the dynamics of the bouncing ball, you can postprocess the simulation results to extract more information. This example postprocesses the simulation results to:

• Find the number of times the ball bounces and the maximum height of each bounce.

• Determine the time of each collision between the ball and the surface using a zero-crossing detection algorithm.

To view the postprocessing code, open the script.

edit("analyzeResult.m")

To run the postprocessing script, call the script.

analyzeResult

Analyze Effect of Damping on Number of Bounces

To see how the amount of damping in the model affects the number of times the ball bounces, plot the number of bounces against the value of the damping coefficient.

plot(c,numbounces,"-o",MarkerEdgeColor="b",LineWidth=1.5)
grid on
title("Number of Bounces vs Damping Coefficient")
xlabel("Damping Coefficient (Ns/m)")
ylabel("Number of Bounces")

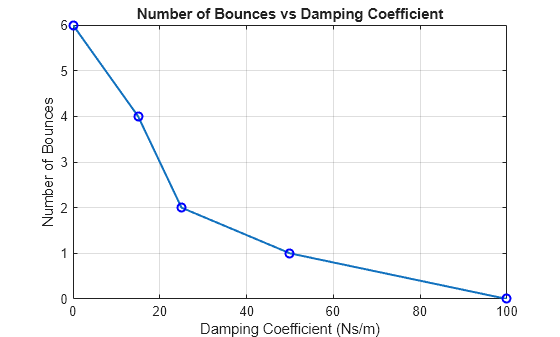
The plot confirms that the number of bounces decreases as the amount of damping in the system increases. When the damping coefficient is large enough, the ball does not bounce at all.

The maximum number of bounces, 6, corresponds to the undamped bouncing ball. The number of bounces for the undamped ball is limited by the duration of the simulation. Because the system has no damping, the ball continues bouncing for as long as you run the simulation. Running a longer simulation would result in a larger number of bounces for the undamped bouncing ball.

Analyze Bounce Timing

To understand how the damping coefficient affects the timing of each bounce, plot the time of each collision between the ball and the surface against the collision number. Because the ball with a damping coefficient of 100 does not bounce, the plot shows data for only four of the five simulated balls.

szs = cellfun(@(c) size(c,1),tcollision);

for idx = 1:length(szs)
    bouncenum = 1:1:szs(idx);
    plot(bouncenum,tcollision{idx},"-o",LineWidth=1.5)
    hold on
end

grid on
legend(legendvals{1:4},Location="best")
xlabel("Collision Number")
ylabel("Time of Collision (seconds)")

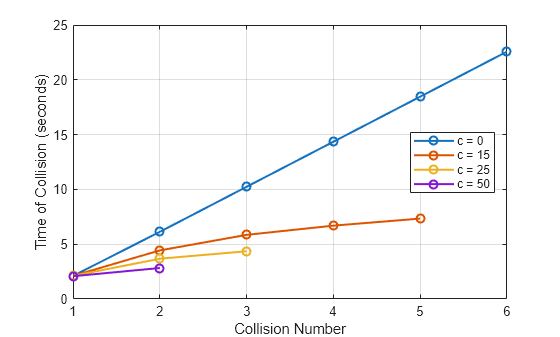
The simulation results for the undamped bouncing ball show a linear relationship between the collision number and the time of the collision. The linear relationship indicates that the time between collisions is constant for the undamped bouncing ball.

As the amount of damping increases, the relationship between the collision number and the time of the collision becomes increasingly nonlinear, and the ball spends less and less time in the air between each successive bounce. The nonlinearity in the restoring force causes the nonlinearity in the bounce timing when damping is present in the system.

To further explore the effect of the nonlinearity in the restoring force, you can run another simulation to analyze the impact of the model parameter $\alpha$.

1. Specify a single, scalar value for the damping coefficient $\mathit{c}$.

2. Specify a vector of several scalar values for $\alpha$.

3. Simulate the model and repeat the analysis of the simulation results.