Group Delay and Phase Delay
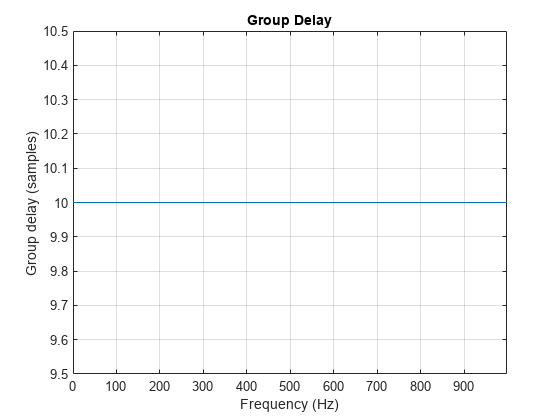
The group delay of a filter is a measure of the average time delay of the filter as a function of frequency. The group delay is defined as the negative first derivative of the filter's phase response. If the complex frequency response of a filter is , then the group delay is
,
where is the phase, or argument, of . Use the grpdelay function to compute group delay of a filter. For example, verify that, for a linear-phase FIR filter, the group delay is one-half the filter order.
fs = 2000; b = fir1(20,200/(fs/2)); islinphase(b)
ans = logical
1
grpdelay(b,1,[],fs)
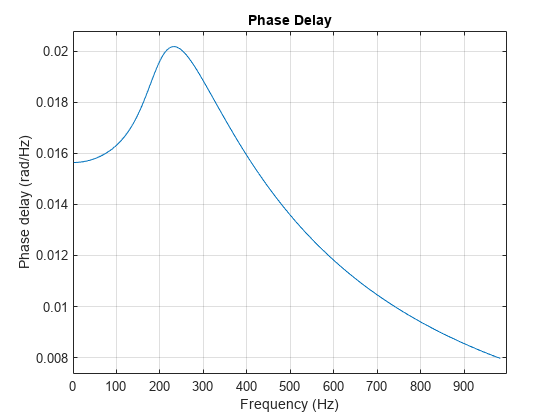
The phase delay of a filter is defined as the negative of the phase divided by the frequency:
.
Use the phasedelay function to compute the phase delay of a filter. For the linear-phase FIR filter of the previous example, the phase delay is equal to the group delay.
phasedelay(b,1,[],fs)

Plot the group delay and the phase delay of a fifth-order Butterworth lowpass filter.
[b,a] = butter(5,200/(fs/2)); grpdelay(b,a,[],fs)

phasedelay(b,a,[],fs)