impinvar
Impulse invariance method for analog-to-digital filter conversion
Description
Examples
Input Arguments
Output Arguments
Algorithms
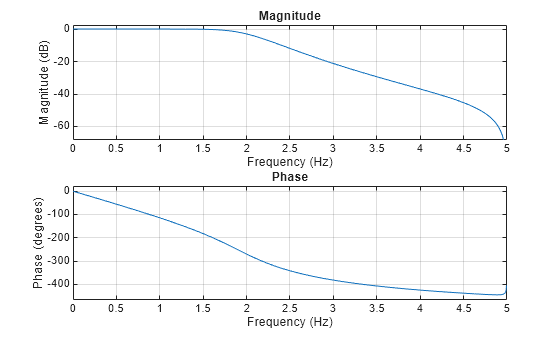
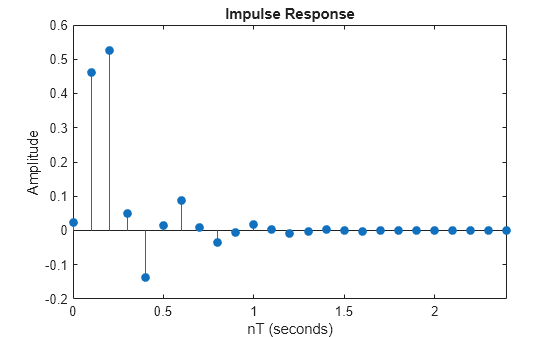
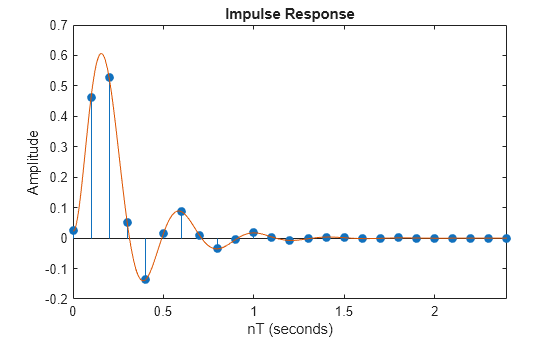
impinvar performs the impulse-invariant method of analog-to-digital
transfer function conversion discussed in reference [2]:
It finds the partial fraction expansion of the system represented by
banda.It replaces the poles
pby the polesexp(p/fs).It finds the transfer function coefficients of the system from the residues from step 1 and the poles from step 2.
References
[1] Antoniou, Andreas. Digital Filters. New York: McGraw-Hill, Inc., 1993.
[2] Parks, Thomas W., and C. Sidney Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987.
Version History
Introduced before R2006a