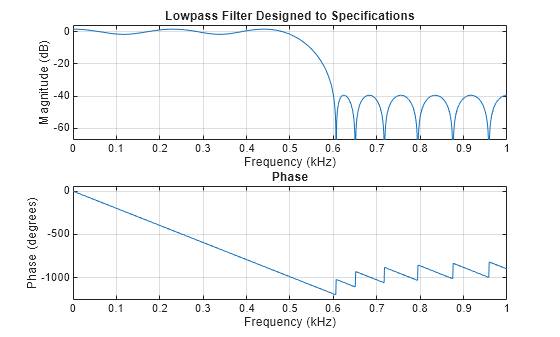
firpmord

Parks-McClellan optimal FIR filter order estimation

Syntax

[n,fo,ao,w] = firpmord(f,a,dev)

[___] = firpmord(___,fs)

c = firpmord(___,"cell")

Description

[n,fo,ao,w] = firpmord(f,a,dev) returns the order estimate n, normalized frequency band edges fo, frequency band amplitudes ao, and weights w that meet input specifications f, a, and dev.

[___] = firpmord(___,fs) specifies a sample rate fs. fs defaults to 2 Hz, implying a Nyquist frequency of 1 Hz.

c = firpmord(___,"cell") returns a cell array c whose elements are the parameters to firpm.

Examples

Minimum-Order Lowpass Filter

Design a minimum-order lowpass filter with a 500 Hz passband cutoff frequency and 600 Hz stopband cutoff frequency. Specify a sample rate of 2000 Hz. Require at least 40 dB of attenuation in the stopband and less than 3 dB of ripple in the passband.

rp = 3;           % Passband ripple in dB 
rs = 40;          % Stopband ripple in dB
fs = 2000;        % Sample rate
f = [500 600];    % Cutoff frequencies
a = [1 0];        % Desired amplitudes

Convert the deviations to linear units. Design the filter and visualize its magnitude and phase responses.

dev = [(10^(rp/20)-1)/(10^(rp/20)+1) 10^(-rs/20)]; 
[n,fo,ao,w] = firpmord(f,a,dev,fs);
b = firpm(n,fo,ao,w);
freqz(b,1,1024,fs)
title("Lowpass Filter Designed to Specifications")

The filter falls slightly short of meeting the stopband attenuation and passband ripple specifications. Using n+1 instead of n in the call to firpm achieves the desired amplitude characteristics.

Parks-McClellan Order of Lowpass Filter

Design a lowpass filter with a 1500 Hz passband cutoff frequency and a 2000 Hz stopband cutoff frequency. Specify a sample rate of 8000 Hz. Require a maximum stopband amplitude of 0.1 and a maximum passband error (ripple) of 0.01.

[n,fo,ao,w] = firpmord([1500 2000],[1 0],[0.01 0.1],8000);
b = firpm(n,fo,ao,w);

Obtain an equivalent result by having firpmord generate a cell array. Visualize the frequency response of the filter.

c = firpmord([1500 2000],[1 0],[0.01 0.1],8000,"cell");
B = firpm(c{:});
freqz(B,1,1024,8000)

Input Arguments

f — Frequency band edges

real-valued vector with even number of elements

Frequency band edges, specified as a real-valued vector with an even number of elements. The argument must be in the range [0, F_s/2], where F_s is the Nyquist frequency. The number of elements in the vector is always a multiple of 2. The frequencies must be in increasing order.

a — Desired amplitude

vector

Desired amplitudes at the points contained in f, specified as a vector. f and a must satisfy the condition length(f) = 2length(a) – 2.

dev — Maximum allowable deviation

vector

Maximum allowable deviation, specified as a vector with the same size as a and with elements the range within the interval (0; 1).

This argument specifies the maximum deviation or ripple between the desired amplitudes for each band and the amplitude response of the estimated Parks-McClellan optimal FIR filter.

fs — Sample rate

2 Hz (default) | real scalar

Sample rate, specified as a real scalar.

Output Arguments

n — Filter order estimate

nonnegative integer

Filter order estimate, returned as a nonnegative integer.

fo — Normalized frequency points

real-valued vector

Normalized frequency points, specified as a real-valued vector. The argument must be in the range [0, 1] , where 1 corresponds to the Nyquist frequency. The number of elements in the vector is always a multiple of 2. The frequencies must be in increasing order.

ao — Amplitude response

real-valued vector

Amplitude response, returned as a real-valued vector.

w — weights

real-valued vector

Weights used to adjust the fit in each frequency band, specified as a real-valued vector. The length of w is half the length of f and a, so there is exactly one weight per band.

c — FIR filter parameters

cell array

FIR filter parameters, returned as a cell array.

Algorithms

The firpmord function uses the algorithm presented in [1]. This function produces inaccurate results for band edges close to either 0 or the Nyquist frequency, fs/2.

Note

• In some cases, firpmord underestimates or overestimates the order n. If the filter does not meet the specifications, try a higher order such as n+1 or n+2.

• In some cases, the algorithm estimates a negative value for the filter order. If that happens, the function returns n as 0.

References

[1] Rabiner, Lawrence R., and Otto Herrmann. “The Predictability of Certain Optimum Finite-Impulse-Response Digital Filters.” IEEE^® Transactions on Circuit Theory. Vol.  20, Number 4, 1973, pp. 401–408.

[2] Rabiner, Lawrence R., and Bernard Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975, pp. 156–157.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

All inputs must be constants. Expressions or variables are allowed if their values do not change.

Version History

Introduced before R2006a