fillgaps
Fill gaps using autoregressive modeling
Description
fillgaps(___) with no output
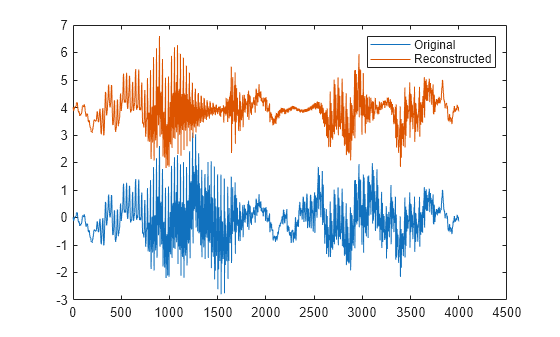
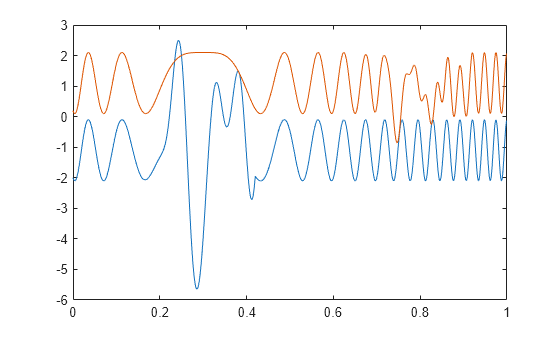
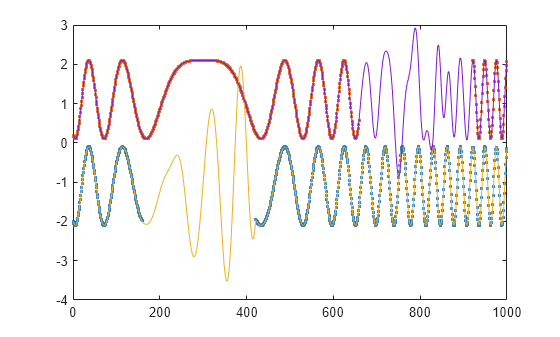
arguments plots the original samples and the reconstructed signal.
This syntax accepts any input arguments from previous syntaxes.
Examples
Input Arguments
Output Arguments
References
[1] Akaike, Hirotugu. "Fitting Autoregressive Models for Prediction." Annals of the Institute of Statistical Mathematics. Vol. 21, 1969, pp. 243–247.
[2] Kay, Steven M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice Hall, 1988.
[3] Orfanidis, Sophocles J. Optimum Signal Processing: An Introduction. 2nd Edition. New York: McGraw-Hill, 1996.
Extended Capabilities
Version History
Introduced in R2016a