falltime
Fall time of negative-going bilevel waveform transitions
Syntax
Description
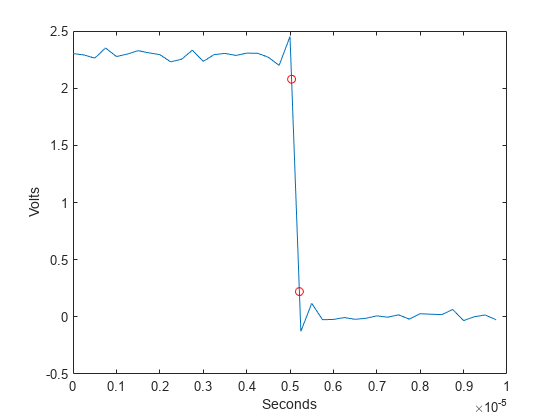
f = falltime(x)f containing the time it takes each
transition of the bilevel waveform x to cross from the 90%
reference level to the 10% reference level.
Note
Because falltime uses interpolation,
f may contain values that do not correspond to
sampling instants of the bilevel waveform x.
[___] = falltime(___,
returns the fall times with additional options specified by one or more
name-value arguments.Name=Value)
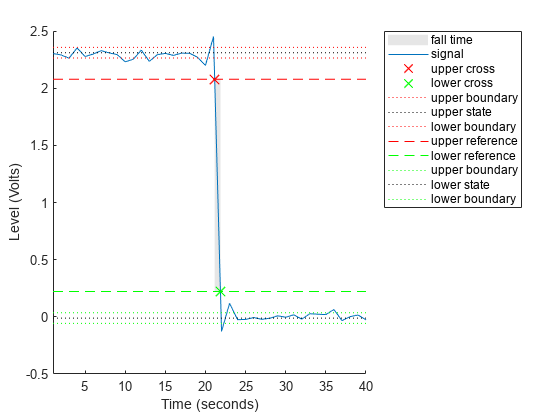
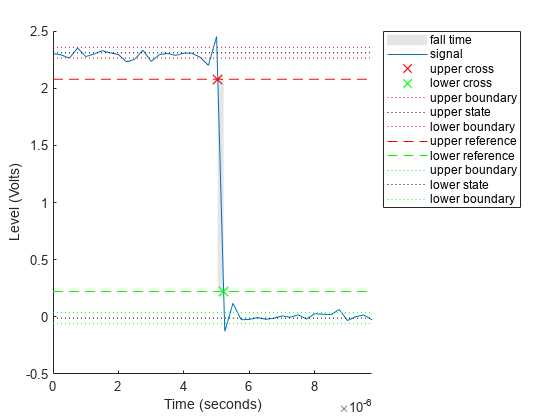
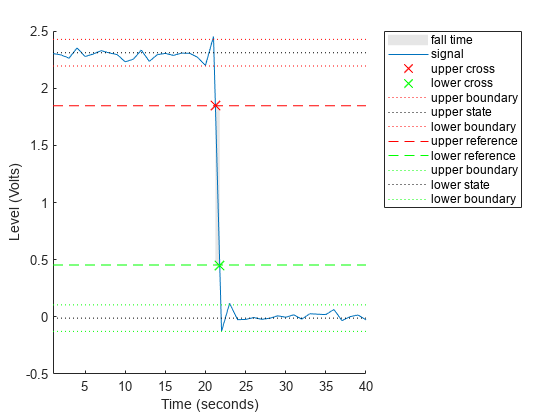
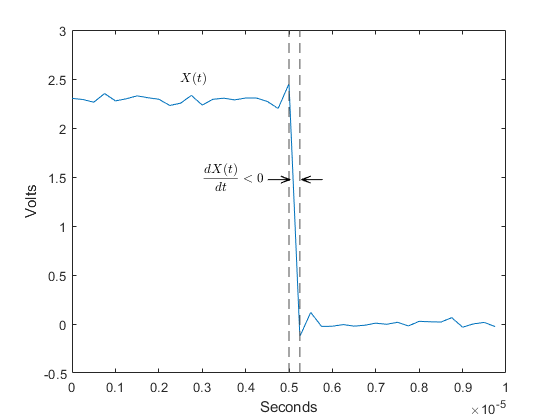
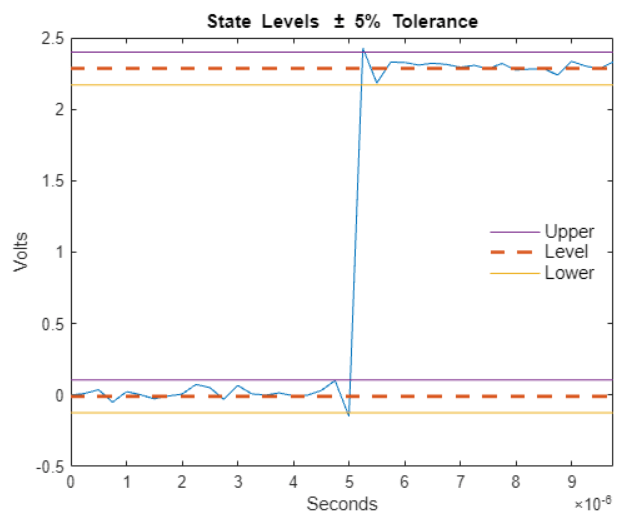
falltime(___) plots the signal and darkens
the regions of each transition where fall time is computed. The plot marks the
lower and upper crossings and the associated reference levels. The plot also
displays the state levels and the associated lower- and upper-state
boundaries.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] IEEE® Standard on Transitions, Pulses, and Related Waveforms, IEEE Standard 181, 2003, pp. 15–17.
Extended Capabilities
Version History
Introduced in R2012a