dutycycle
Duty cycle of pulse waveform
Syntax
Description
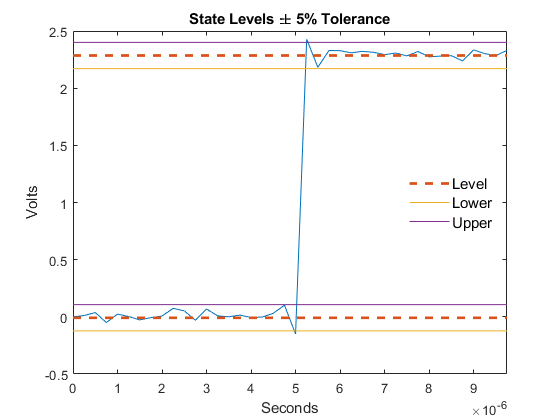
d = dutycycle(x)dutycycle estimates the state levels of x
by a histogram method. The low-state and high-state boundaries are expressed as the state
level plus or minus a scalar multiple of the difference between the state levels. See
State-Level Tolerances for more details.
[
with any input arguments from previous syntaxes also returns:d,initcross,finalcross,nextcross,midlev]
= dutycycle(___)
A vector,
initcross, whose elements correspond to the mid-crossings (mid-reference level instants) of the initial transition of each pulse with a correspondingnextcross.A vector,
finalcross, whose elements correspond to the mid-crossings (mid-reference level instants) of the final transition of each pulse with a correspondingnextcross.A vector,
nextcross, whose elements correspond to the mid-crossings (mid-reference level instants) of the next detected transition for each pulse.A scalar,
midlev, that corresponds to the mid-reference level.
[___]
= dutycycle(___,
returns the ratio of pulse width to pulse period with additional options specified by one
or more Name,Value)Name,Value pair arguments.
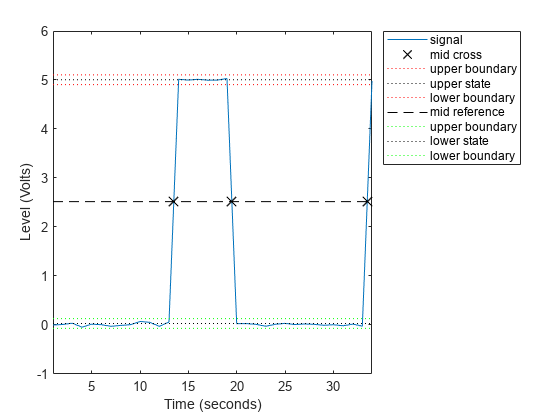
dutycycle(___) plots the waveform, the location of
the mid-reference level instants, the associated reference levels, the state levels, and
the associated lower and upper state boundaries.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Skolnik, M. I. Introduction to Radar Systems. New York, NY: McGraw-Hill, 1980.
[2] IEEE® Standard on Transitions, Pulses, and Related Waveforms. IEEE Standard 181, 2003.
Extended Capabilities
Version History
Introduced in R2012a