dopplerShiftCircularOrbit
Calculate Doppler shift at ground station due to circularly orbiting satellite
Since R2024a
Syntax
Description
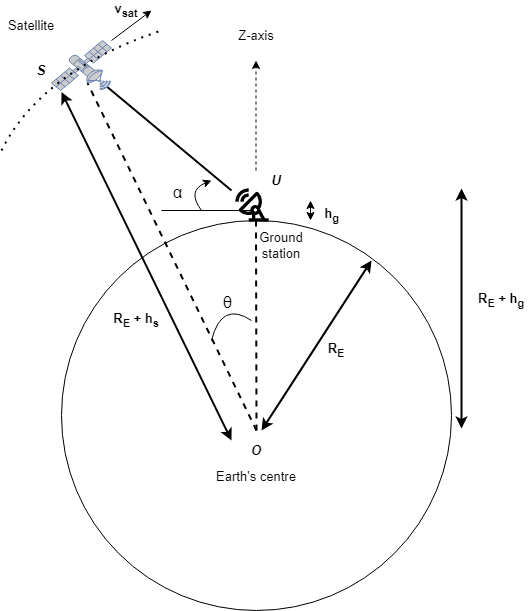
shift = dopplerShiftCircularOrbit(el,hs,hg,freq)el, satellite altitude
hs, ground station altitude hg, and satellite
carrier frequency freq.
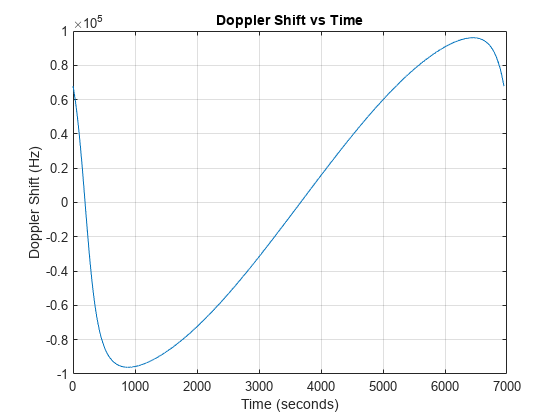
For more information, see Doppler Shift Calculations.
Note
dopplerShiftCircularOrbit assumes:
The Earth is spherical, the ground station is static, and that the Earth does not rotate.
An access or link is possible from the satellite to the ground station at all times.
The ground station is located at the North Pole (positive Z–axis), and the satellite starts from the initial input elevation angle
elin the second quadrant of the YZ–plane.Satellite moves in the clockwise direction in its circular orbit.
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2024a