makeweight
Weighting function with monotonic gain profile
Syntax
Description
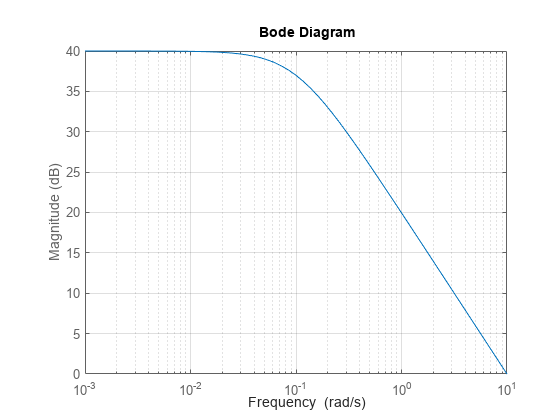
makeweight is a convenient way to
specify loop shapes, target gain profiles, or weighting functions
for applications such as controller synthesis and control system tuning.
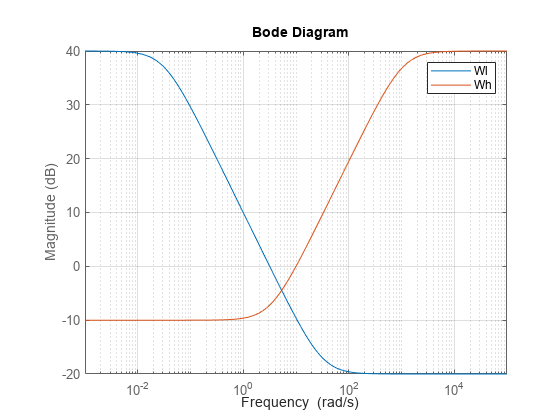
creates a first-order, continuous-time weight W(s) satisfying these constraints:W = makeweight(dcgain,[freq,mag],hfgain)
In other words, the gain of W passes through
mag at the finite frequency freq.
W = makeweight(dcgain,[freq,mag],hfgain,Ts)
In other words, the gain of W passes through
mag at the frequency freq. The
frequency freq must satisfy 0 < freq <
π/Ts.
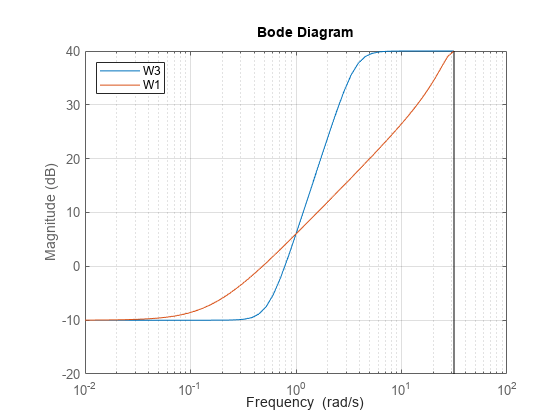
W = makeweight(dcgain,wc,hfgain,___)wc. This syntax is
equivalent to setting [freq,mag] to [wc,1].
You can use this syntax with any of the previous input-argument combinations to
create a continuous-time, discrete-time, or Butterworth weighting function.
Examples
Input Arguments
Output Arguments
Version History
Introduced before R2006a
See Also
hinfstruct | hinfsyn | mixsyn | musyn | mkfilter | augw | TuningGoal.LoopShape