H-Infinity Performance
One approach to characterizing closed-loop performance objectives is to measure the size of certain closed-loop transfer function matrices using various matrix norms. As described in Interpretation of H2 and H-Infinity Norms, matrix norms provide a measure of how large output signals can get for certain classes of input signals. Optimizing these types of performance objectives over the set of stabilizing controllers is the main thrust of recent optimal control theory, such as L1, H2, H∞, and optimal control. Hence, it is important to understand how many types of control objectives can be posed as a minimization of closed-loop transfer functions.
Performance as Generalized Disturbance Rejection
Consider a tracking problem, with disturbance rejection, measurement noise, and control input signal limitations, as shown in Generalized and Weighted Performance Block Diagram. K is some controller to be designed and G is the system you want to control.
Typical Closed-Loop Performance Objective

A reasonable, though not precise, design objective would be to design K to keep tracking errors and control input signal small for all reasonable reference commands, sensor noises, and external force disturbances.
Hence, a natural performance objective is the closed-loop gain from exogenous influences (reference commands, sensor noise, and external force disturbances) to regulated variables (tracking errors and control input signal). Specifically, let T denote the closed-loop mapping from the outside influences to the regulated variables:

You can assess performance by measuring the gain from outside influences to regulated variables. In other words, good performance is associated with T being small. Because the closed-loop system is a multi-input, multi-output (MIMO) dynamic system, there are two different aspects to the gain of T:
Spatial (vector disturbances and vector errors)
Temporal (dynamic relationship between input/output signals)
Hence the performance criterion must account for
Relative magnitude of outside influences
Frequency dependence of signals
Relative importance of the magnitudes of regulated variables
So if the performance objective is in the form of a matrix norm, it should actually be a weighted norm
∥WLTWR∥
Interconnection with Typical MIMO Performance Objectives
The closed-loop performance objectives are formulated as weighted closed-loop transfer functions that are to be made small through feedback. A generic example, which includes many relevant terms, is shown in block diagram form in Generalized and Weighted Performance Block Diagram. In the diagram, G denotes the plant model and K is the feedback controller.
Generalized and Weighted Performance Block Diagram
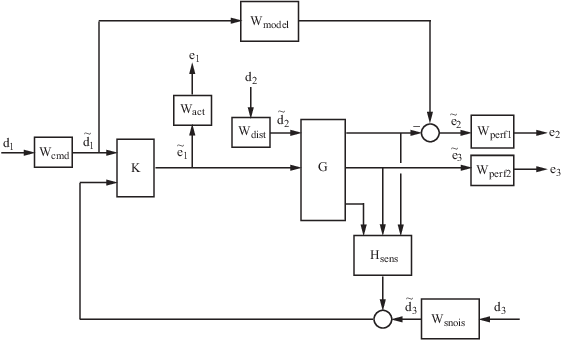
The blocks in this figure might be scalar (SISO) and/or multivariable (MIMO), depending on the specific example. The mathematical objective of H∞ control is to make the closed-loop MIMO transfer function Ted satisfy ∥Ted∥∞ < 1. The weighting functions are used to scale the input/output transfer functions such that when ∥Ted∥∞ < 1, the relationship between and is suitable.
Performance requirements on the closed-loop system are transformed into the H∞ framework with the help of weighting or scaling functions. Weights are selected to account for the relative magnitude of signals, their frequency dependence, and their relative importance. This is captured in the figure above, where the weights or scalings [Wcmd, Wdist,Wsnois] are used to transform and scale the normalized input signals [d1,d2,d3] into physical units defined as [d1, d2, d3]. Similarly weights or scalings [Wact, Wperf1,Wperf2] transform and scale physical units into normalized output signals [e1, e2, e3].
When you use systune, you specify performance objectives
using TuningGoal objects. The systune
command converts these objectives to frequency-dependent weighting functions and
appends them to the tunable model of your system at the appropriate signal
locations. The command then tunes the model parameters to minimize the overall
H∞ norm of the resulting
MIMO augmented system. When you use hinfstruct, you
construct the weighting functions and append them in appropriate locations
yourself.
The following table contains an interpretation of the signals, weighting functions, and models.
|
Signal |
Meaning |
|---|---|
|
d1
|
Normalized reference command Typical reference command in physical units |
|
d2
|
Normalized exogenous disturbances Typical exogenous disturbances in physical units |
|
d3
|
Normalized sensor noise Typical sensor noise in physical units |
|
e1
|
Weighted control signals Actual control signals in physical units |
|
e2
|
Weighted tracking errors Actual tracking errors in physical units |
|
e3
|
Weighted plant errors Actual plant errors in physical units |
Wcmd
Wcmd is included in H∞ control problems that require tracking of a reference command. Wcmd shapes the normalized reference command signals (magnitude and frequency) into the actual (or typical) reference signals that you expect to occur. It describes the magnitude and the frequency dependence of the reference commands generated by the normalized reference signal. Normally Wcmd is flat at low frequency and rolls off at high frequency. For example, in a flight control problem, fighter pilots generate stick input reference commands up to a bandwidth of about 2 Hz. Suppose that the stick has a maximum travel of three inches. Pilot commands could be modeled as normalized signals passed through a first-order filter:
Wmodel
Wmodel represents a desired ideal model for the closed-looped system and is often included in problem formulations with tracking requirements. Inclusion of an ideal model for tracking is often called a model matching problem, i.e., the objective of the closed-loop system is to match the defined model. For good command tracking response, you might want the closed-loop system to respond like a well-damped second-order system. The ideal model would then be
for specific desired natural frequency ω and desired damping ratio ζ. Unit conversions might be necessary to ensure exact correlation between the ideal model and the closed-loop system. In the fighter pilot example, suppose that roll-rate is being commanded and 10º/second response is desired for each inch of stick motion. Then, in these units, the appropriate model is:
Wdist
Wdist shapes the frequency content and magnitude of the exogenous disturbances affecting the plant. For example, consider an electron microscope as the plant. The dominant performance objective is to mechanically isolate the microscope from outside mechanical disturbances, such as ground excitations, sound (pressure) waves, and air currents. You can capture the spectrum and relative magnitudes of these disturbances with the transfer function weighting matrix Wdist.
Wperf1
Wperf1 weights the difference between the response of the closed-loop system and the ideal model W model. Often you might want accurate matching of the ideal model at low frequency and require less accurate matching at higher frequency, in which case Wperf1 is flat at low frequency, rolls off at first or second order, and flattens out at a small, nonzero value at high frequency. The inverse of the weight is related to the allowable size of tracking errors, when dealing with the reference commands and disturbances described by Wcmd and Wdist.
Wperf2
Wperf2 penalizes variables internal to the process G, such as actuator states that are internal to G or other variables that are not part of the tracking objective.
Wact
Wact is used to shape the penalty on control signal use. Wact is a frequency varying weighting function used to penalize limits on the deflection/position, deflection rate/velocity, etc., response of the control signals, when dealing with the tracking and disturbance rejection objectives defined above. Each control signal is usually penalized independently.
Wsnois
Wsnois represents frequency domain models of sensor noise. Each sensor measurement feedback to the controller has some noise, which is often higher in one frequency range than another. The Wsnois weight tries to capture this information, derived from laboratory experiments or based on manufacturer measurements, in the control problem. For example, medium grade accelerometers have substantial noise at low frequency and high frequency. Therefore the corresponding Wsnois weight would be larger at low and high frequency and have a smaller magnitude in the mid-frequency range. Displacement or rotation measurement is often quite accurate at low frequency and in steady state, but responds poorly as frequency increases. The weighting function for this sensor would be small at low frequency, gradually increase in magnitude as a first- or second-order system, and level out at high frequency.
Hsens
Hsens represents a model of the sensor dynamics or an external antialiasing filter. The transfer functions used to describe Hsens are based on physical characteristics of the individual components. These models might also be lumped into the plant model G.
This generic block diagram has tremendous flexibility and many control performance objectives can be formulated in the H∞ framework using this block diagram description.
Robustness in the H-Infinity Framework
Performance and robustness tradeoffs in control design were discussed in the context of multivariable loop shaping in Tradeoff Between Performance and Robustness. In the H∞ control design framework, you can include robustness objectives as additional disturbance to error transfer functions — disturbances to be kept small. Consider the following figure of a closed-loop feedback system with additive and multiplicative uncertainty models.
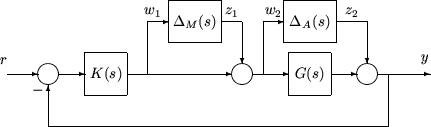
The transfer function matrices are defined as:
where TI(s) denotes the input complementary sensitivity function and SO(s) denotes the output sensitivity function. Bounds on the size of the transfer function matrices from z1 to w1 and z2 to w2 ensure that the closed-loop system is robust to multiplicative uncertainty, ΔM(s), at the plant input, and additive uncertainty, ΔA(s), around the plant G(s). In the H∞ control problem formulation, the robustness objectives enter the synthesis procedure as additional input/output signals to be kept small. The interconnection with the uncertainty blocks removed follows.
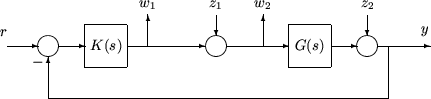
The H∞ control robustness objective is now in the same format as the performance objectives, that is, to minimize the H∞ norm of the transfer matrix from z, [z1,z2], to w, [w1,w2].
Weighting or scaling matrices are often introduced to shape the frequency and magnitude content of the sensitivity and complementary sensitivity transfer function matrices. Let WM correspond to the multiplicative uncertainty and WA correspond to the additive uncertainty model. ΔM(s) and ΔA(s) are assumed to be a norm bounded by 1, i.e., |ΔM(s)|<1 and |ΔA(s)|<1. Hence as a function of frequency, |WM(jω)| and |WA(jω)| are the respective sizes of the largest anticipated additive and multiplicative plant perturbations.
The multiplicative weighting or scaling WM represents a percentage error in the model and is often small in magnitude at low frequency, between 0.05 and 0.20 (5% to 20% modeling error), and growing larger in magnitude at high frequency, 2 to 5 ((200% to 500% modeling error). The weight will transition by crossing a magnitude value of 1, which corresponds to 100% uncertainty in the model, at a frequency at least twice the bandwidth of the closed-loop system. A typical multiplicative weight is
By contrast, the additive weight or scaling WA represents an absolute error that is often small at low frequency and large in magnitude at high frequency. The magnitude of this weight depends directly on the magnitude of the plant model, G(s).
Numeric Considerations
Do not choose weighting functions with poles very close to s = 0 (z = 1 for discrete-time systems). For instance, although it might seem sensible to choose Wcmd = 1/s to enforce zero steady-state error, doing so introduces an unstable pole that cannot be stabilized, causing synthesis to fail. Instead, choose Wcmd = 1/(s + δ). The value δ must be small but not very small compared to system dynamics. For instance, for best numeric results, if your target crossover frequency is around 1 rad/s, choose δ = 0.0001 or 0.001. Similarly, in discrete time, choose sample times such that system and weighting dynamics are not more than a decade or two below the Nyquist frequency.
See Also
hinfstruct | hinfsyn | mixsyn