hyperbolicPenalty
Hyperbolic penalty value for a point with respect to a bounded region
Since R2021b
Description
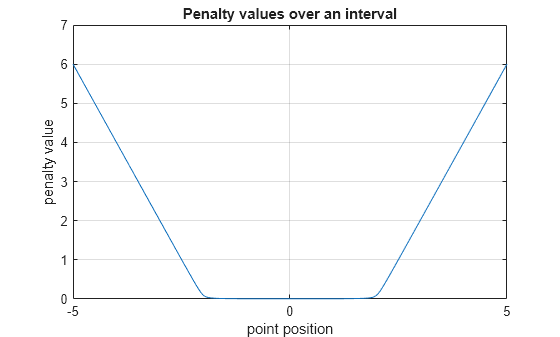
p = hyperbolicPenalty(x,xmin,xmax)p for the point
x with respect to the region bounded by xmin and
xmax. p has the same dimension as
x. This syntax uses the default values of 1 and
0.1 for the lambda and tau
parameters of the hyperbolic function, respectively.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2021b