twoRayChannel
Description
The twoRayChannel
System object™ models a narrowband two-ray propagation channel. A two-ray propagation
channel is the simplest type of multipath channel. You can use a two-ray channel to
simulate propagation of signals in a homogeneous, isotropic medium with a single
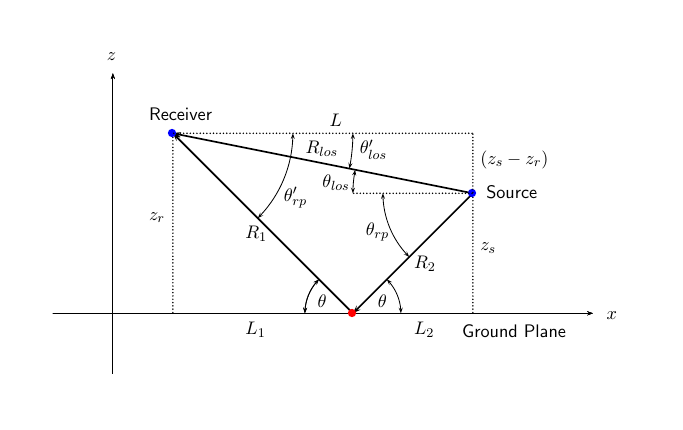
reflecting boundary. This type of medium has two propagation paths: a line-of-sight
(direct) propagation path from one point to another and a ray path reflected from the
boundary. You can use the twoRayChannel object for short-range radar and
mobile communications applications where the signals propagate along straight paths and
the earth is assumed to be flat. You can also use this object for sonar and microphone
applications. For acoustic applications, you can choose the fields to be non-polarized
and adjust the propagation speed to be the speed of sound in air or water. You can use
twoRayChannel to model propagation from several points
simultaneously.
While the twoRayChannel object works for all frequencies, the
attenuation models for atmospheric gases and rain are valid for electromagnetic signals
in the frequency range 1–1000 GHz only. The attenuation model for fog and clouds is
valid for 10–1000 GHz. Outside these frequency ranges, the twoRayChannel
object uses the nearest valid value.
The twoRayChannel object applies range-dependent time delays to the
signals, and as well as gains or losses, phase shifts, and boundary reflection loss. The
twoRayChannel object also applies Doppler shift when either the
source or destination is moving.
Signals at the channel output can be kept separate or be
combined — controlled by the
CombinedRaysOutput property. In the
separate option, both fields arrive at the destination
separately and are not combined. For the combined option, the two
signals at the source propagate separately but are coherently summed at the destination
into a single quantity. This option is convenient when the difference between the sensor
or array gains in the directions of the two paths is not significant and need not be
taken into account.
Unlike the phased.FreeSpace
System object, the twoRayChannel
System object does not support two-way propagation.
To perform two-ray channel propagation:
Create the
twoRayChannelobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
channel = twoRayChannelchannel
System object.
channel = twoRayChannel(Name=Value)channel
System object with each specified property Name set to the
corresponding Value. You can specify additional pairs of
arguments in any order as
Name1=Value1,...,NameN=ValueN.
Properties
Usage
Description
prop_sig = channel(sig,origin_pos,dest_pos,origin_vel,dest_vel)prop_sig, when a narrowband
signal, sig, propagates through a two-ray channel from the
origin_pos position to the
dest_pos position. Either the
origin_pos or dest_pos arguments
can have multiple points but you cannot specify both as having multiple points.
The velocity of the signal origin is specified in
origin_vel and the velocity of the signal destination
is specified in dest_vel. The dimensions of
origin_vel and dest_vel must agree
with the dimensions of origin_pos and
dest_pos, respectively.
Electromagnetic fields propagated through a two-ray channel can be polarized
or nonpolarized. For, nonpolarized fields, such as an acoustic field, the
propagating signal field, sig, is a vector or matrix. When
the fields are polarized, sig is an array of structures.
Every structure element represents an electric field vector in Cartesian
form.
In the two-ray environment, there are two signal paths connecting every signal origin and destination pair. For N signal origins (or N signal destinations), there are 2N number of paths. The signals for each origin-destination pair do not have to be related. The signals along the two paths for any single source-destination pair can also differ due to phase or amplitude differences.
You can keep the two signals at the destination separate
or combined — controlled by the
CombinedRaysOutput property.
Combined means that the signals at the source propagate
separately along the two paths but are coherently summed at the destination into
a single quantity. To use the separate option, set
CombinedRaysOutput to false. To use
the combined option, set
CombinedRaysOutput to true. This
option is convenient when the difference between the sensor or array gains in
the directions of the two paths is not significant and need not be taken into
account.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
References
[1] Saakian, A. Radio Wave Propagation Fundamentals. Norwood, MA: Artech House, 2011.
[2] Balanis, C. Advanced Engineering Electromagnetics. New York: Wiley & Sons, 1989.
[3] Rappaport, T. Wireless Communications: Principles and Practice, 2nd Ed New York: Prentice Hall, 2002.
[4] Radiocommunication Sector of the International Telecommunication Union. Recommendation ITU-R P.676-12: Attenuation by atmospheric gases. 2019.
[5] Radiocommunication Sector of the International Telecommunication Union. Recommendation ITU-R P.840-6: Attenuation due to clouds and fog. 2013.
[6] Radiocommunication Sector of the International Telecommunication Union. Recommendation ITU-R P.838-3: Specific attenuation model for rain for use in prediction methods. 2005.
Extended Capabilities
Version History
Introduced in R2021a