surfaceReflectivityLand
Description
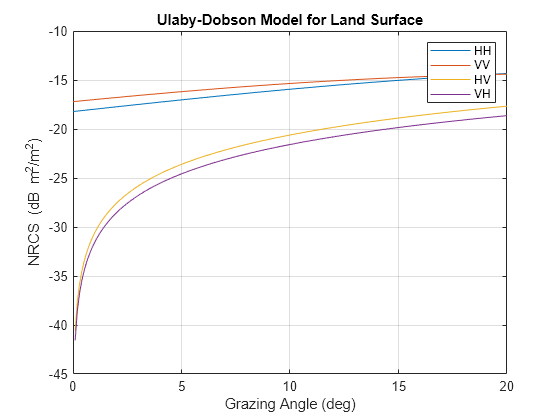
This System object™ computes the normalized reflectivity of a land surface. Normalized reflectivity is the radar cross-section of a unit area of a surface. Multiplying by the total area of a surface or the illuminated area of a surface gives the total radar cross-section. Normalized reflectivity is also referred to as surface σ0 and is a function of frequency and grazing angle.
To compute the normalized reflectivity:
Create the
surfaceReflectivityLandobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
refl = surfaceReflectivityLandrefl for a land surface. Use this
object to generate a normalized radar cross section (NRCS). This syntax creates a
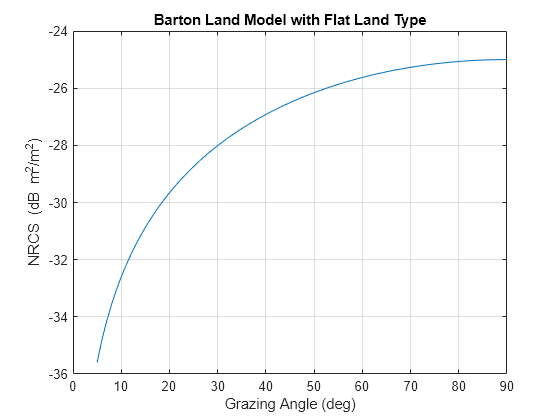
normalized reflectivity object with a 'Barton' land
Model and a 'Flatland'
LandType.
It is not recommended to use models outside of their defined validity regions. See
the Model property description for more information about available
models and at what frequency and grazing angles the models are valid. See the
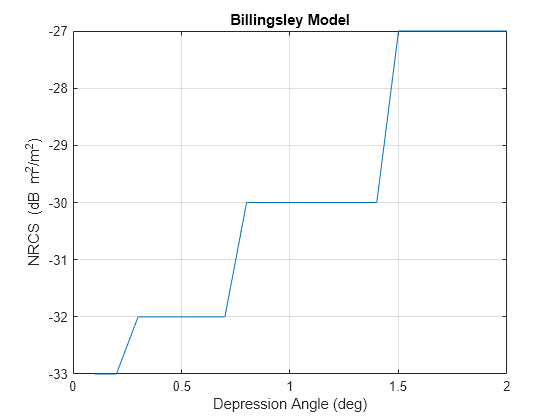
LandType property help for information about applicable land types
for each model.
refl = surfaceReflectivityLand(Name=Value)Name set to the specified Value. You can
specify additional name-value pair arguments in any order as
(Name1=Value1, … ,NameN=ValueN).
Example: refl =
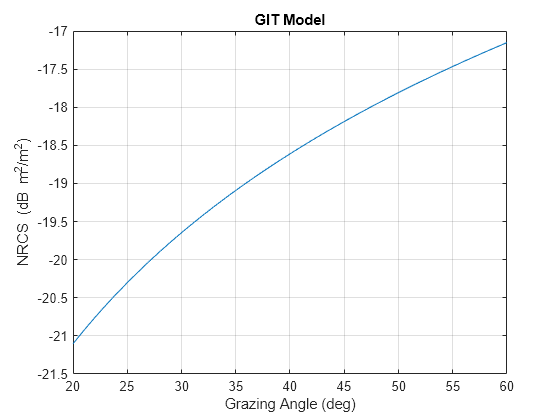
surfaceReflectivityLand(Model="GIT",LandType="Soil",SurfaceHeightStandardDeviation=1)
creates a normalized reflectivity object for land using the GIT model with a
LandType of Soil and a
SurfaceHeightStandardDeviation of 1.
Properties
Usage
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
References
[1] Barton, David Knox. Radar Equations for Modern Radar. Artech House, 2013.
[2] Long, Maurice W. Radar Reflectivity of Land and Sea. 3rd ed, Artech House, 2001.
[3] Nathanson, Fred E., et al. Radar Design Principles: Signal Processing and the Environment. 2. ed., Repr, Scitech Publ, 2004.
[4] Reilly, J. P., R. L. McDonald, and G. D. Dockery. "RF-Environment Models for the ADSAM Program." Report No. A1A97U-070, Laurel, MD: Johns Hopkins University Applied Physics Laboratory, August 22, 1997.
[5] Billingsley, J. Barrie. Low-Angle Radar Land Clutter: Measurements and Empirical Models. William Andrew Pub. : SciTech Pub. ; Institution of Electrical Engineers, 2002.
[6] Richards, M. A., et al., editors. Principles of Modern Radar. SciTech Pub, 2010.
[7] Morchin, Fred E., J. Patrick Reilly, and Marvin Cohen. Radar Design Principles: Signal Processing and the Environment. 2nd ed. New York: McGraw-Hill, 1991.
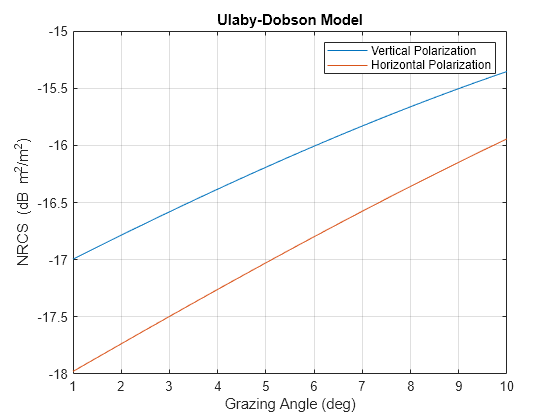
[8] Ulaby, Fawwaz T., and M. Craig Dobson. Handbook of Radar Scattering Statistics for Terrain. Artech House, 1989.
Extended Capabilities
Version History
Introduced in R2022a