rcscylinder
Syntax
Description
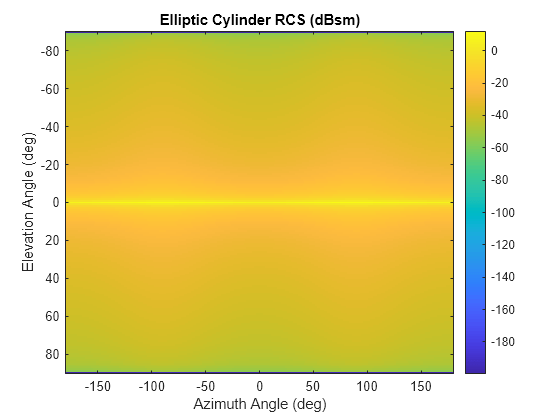
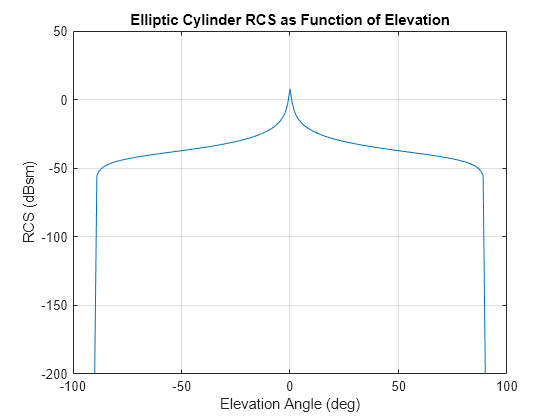
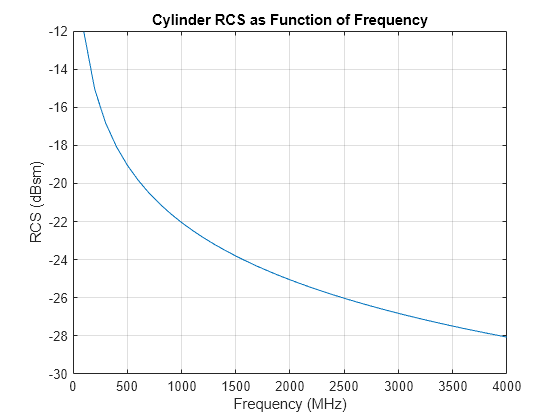
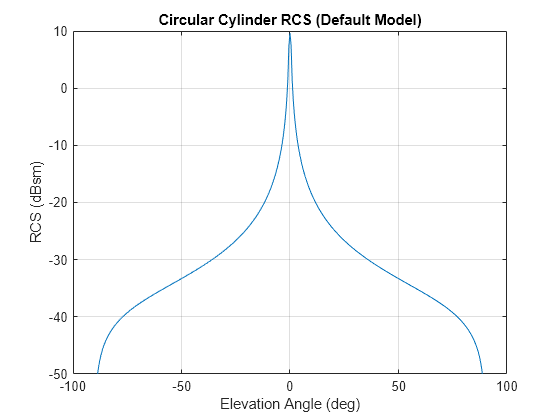
rcspat = rcscylinder(r1,r2,height,c,fc)r1, a semi-minor axis, r2, and a height,
height. The radar cross section is a function of signal frequency,
fc, and signal propagation speed, c. The bottom
of the cylinder lies on the xy-plane. The height of the cylinder points
along the positive z-axis.
Examples
Input Arguments
Output Arguments
More About
References
[1] Crispin, J. W. and A. L. Maffett. Radar Cross-Section Estimation for Simple Shapes. Proceedings of the IEEE 53, no. 8 (August 1965): 833–48.
[2] Knott, Eugene F., John F. Shaffer, and Micahel T. Tuley. Radar Cross Section, 2nd Ed. Raleigh, NC: Scitech Publishing, Inc., 2004.
[3] Mahafza, Bassem. Radar Systems Analysis and Design Using MATLAB, 3rd Ed. Boca Raton, FL: Chapman & Hall/CRC, 2013.
Extended Capabilities
Version History
Introduced in R2021a
See Also
rcsdisc | rcssphere | rcstruncone | phased.BackscatterRadarTarget | phased.RadarTarget