freeSpacePath

Monostatic free space propagation path

Since R2025a

Syntax

propPaths = freeSpacePath(freq,rdrPose,tgtPoses)

propPaths = freeSpacePath(freq,rdrPose,tgtPoses,Name=Value)

Description

propPaths = freeSpacePath(freq,rdrPose,tgtPoses) returns two-way monostatic free space propagation paths for targets.

propPaths = freeSpacePath(freq,rdrPose,tgtPoses,Name=Value) returns two-way monostatic free space propagation paths for targets, with additional options specified using one or more name-value arguments. For example, you can specify transceiver mounting location and angle.

Examples

Free Space Propagation Paths for Radar Transceiver

This example shows how to calculate the free space propagation path for a radar transceiver configuration.

Create a radar transceiver with an isotropic antenna, transmitting a linear frequency modulated (LFM) pulse waveform with a 10 microsecond pulsewidth. Calculate the free space propagation paths assuming the radar is at the origin and the target is 5 km away. Return I/Q signals from the radar transceiver at the initial time and plot the results. Start by initializing the radar transceiver.

wav  = phased.LinearFMWaveform(PulseWidth=1e-5);
ant  = phased.IsotropicAntennaElement;
rdr  = radarTransceiver(Waveform=wav, ...
     TransmitAntenna=phased.Radiator(Sensor=ant), ...
     ReceiveAntenna=phased.Collector(Sensor=ant), ...
     RangeOutputPort=true);
freq = rdr.TransmitAntenna.OperatingFrequency; 

Define the radar position, target position, and target velocity. Calculate the free space propagation paths. The target is located 5 km away and is moving at 20 m/s in the y-direction.

rdrPose.Position = [0 0 0];   % Radar position (m)
tgtPose.Position = [0 5e3 0]; % Target position (m)
tgtPose.Velocity = [0 20 0];  % Target velocity (m/s) 
proppaths        = freeSpacePath(freq,rdrPose,tgtPose)

proppaths = struct with fields:
               PathLength: 10000
                 PathLoss: 191.9392
    ReflectionCoefficient: 11.2177
         AngleOfDeparture: [2×1 double]
           AngleOfArrival: [2×1 double]
             DopplerShift: -40.0277

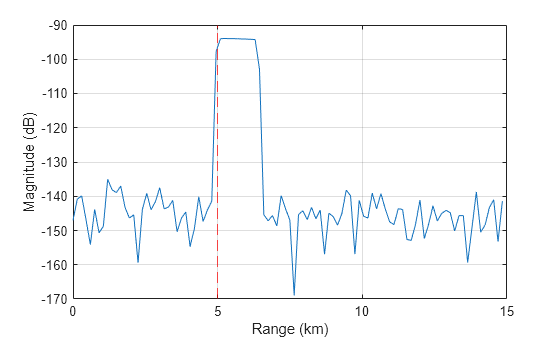
Return I/Q signals from the radarTransceiver at a time of 0 seconds and plot the results. The target is located at 5 km.

t = 0; % Time (sec) 
[iq,rgrid] = rdr(proppaths,t);

% Plot 
figure
plot(rgrid*1e-3,mag2db(abs(sum(iq,2))))
grid on
hold on
xline(5,'r--')
xlabel('Range (km)')
ylabel('Magnitude (dB)')

Free Space Propagation Paths for Rotated Radar Transceiver

This example shows how to calculate the free space propagation path for a rotated radar transceiver configuration.

Create a radar transceiver with a directive sinc antenna with a 5 degree beamwidth. Rotate the radar to point in the direction of the target by modifying the mounting angle. Calculate the free space propagation path assuming the radar is at the origin and the target is 5 km away. The propagation paths calcuated by freeSpacePath are in the radar mounting frame. Return I/Q signals from the radar transceiver at the initial time and plot the results. Start by initializing the radar transceiver.

mntAng = [90 0 0];           % Mounting angles (deg)
wav  = phased.LinearFMWaveform(PulseWidth=1e-5);
ant  = phased.IsotropicAntennaElement;
rdr  = radarTransceiver(Waveform=wav, ...
     TransmitAntenna=phased.Radiator(Sensor=ant), ...
     ReceiveAntenna=phased.Collector(Sensor=ant), ...
     RangeOutputPort=true);
freq = rdr.TransmitAntenna.OperatingFrequency; 

Define the radar position, target position, and target velocity. Calculate the free space propagation path in the radar mounting frame.

rdrPose.Position = [0 0 0];   % Radar position (m)
tgtPose.Position = [0 5e3 0]; % Target position (m)
tgtPose.Velocity = [0 20 0];  % Target velocity (m/s) 
proppaths        = freeSpacePath(freq,rdrPose,tgtPose)

proppaths = struct with fields:
               PathLength: 10000
                 PathLoss: 191.9392
    ReflectionCoefficient: 11.2177
         AngleOfDeparture: [2×1 double]
           AngleOfArrival: [2×1 double]
             DopplerShift: -40.0277

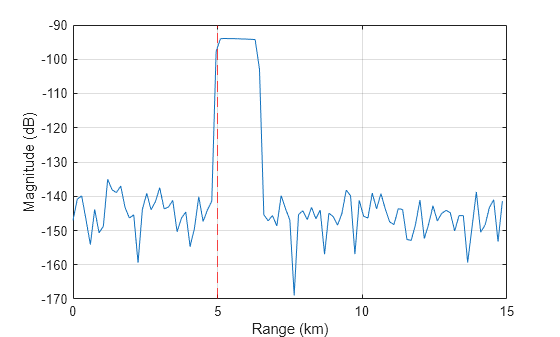
Return I/Q signals from radarTransceiver at a time of 0 seconds and plot the results. The target is located at 5 km.

t = 0;                        % Time (sec) 
[iq,rgrid] = rdr(proppaths,t);

% Plot 
figure
plot(rgrid*1e-3,mag2db(abs(sum(iq,2))))
grid on
hold on
xline(5,'r--')
xlabel('Range (km)')
ylabel('Magnitude (dB)')

Input Arguments

freq — Operating frequency (Hz)

positive scalar

Operating frequency of the radar transceiver, specified as a positive scalar in units of hertz.

Data Types: double

rdrPose — Transceiver platform pose

structure

Transceiver platform pose, specified as a structure that contains Position, Velocity, Orientation, and Signatures fields. You can define platforms as platform objects in a radarScenario and then return the platform position (does not include Signatures) as structures using platformPoses. The Signatures field in rdrPose is not used and is an optional input.

Field	Description
Position	Position of the platform, specified in the global coordinate frame as a real-valued 1-by-3 row vector in the form of [x y z]. Units are in meters (m). There is no default value.
Velocity	Velocity of the platform, specified in the global coordinate frame as a real-valued 1-by-3 row vector in the form of [x y z]. Units are meters per second (m/s). The default value is [0 0 0].
Orientation	Orientation of the platform with respect to the local scenario navigation frame, specified as a unitless scalar quaternion or a 3-by-3 rotation matrix in units of degrees. Orientation defines the frame rotation from the local navigation coordinate system to the current platform body coordinate system. Units are dimensionless. The default value is quaternion(1,0,0,0).
Signatures	Mean monostatic target radar cross section (RCS) signature, specified as a rcsSignature object. Polarimetric signatures are not supported. The default value is the rscSignature object with default values.

Data Types: struct

tgtPoses — Target platform poses

structure | 1-by-T array of structures

Target platform poses, specified as a structure or a 1-by-T array of structures that contain Position, Velocity, Orientation, and Signatures fields for each target, T. You can define platforms as platform objects in a radarScenario and then return the platform position (does not include Signatures) as structures using platformPoses.

Field	Description
Position	Position of the platform, specified in the global coordinate frame as a real-valued 1-by-3 row vector in the form of [x y z]. Units are in meters (m). There is no default value.
Velocity	Velocity of the platform, specified in the global coordinate frame as a real-valued 1-by-3 row vector in the form of [x y z]. Units are meters per second (m/s). The default value is [0 0 0].
Orientation	Orientation of the platform with respect to the local scenario navigation frame, specified as a unitless scalar quaternion or a 3-by-3 rotation matrix in units of degrees. Orientation defines the frame rotation from the local navigation coordinate system to the current platform body coordinate system. Units are dimensionless. The default value is quaternion(1,0,0,0).
Signatures	Mean monostatic target radar cross section (RCS) signature, specified as a rcsSignature object. Polarimetric signatures are not supported. The default value is the rscSignature object with default values.

Data Types: struct

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: propPaths = freeSpacePath(txPose,rxPose,tgtPoses,IncludeDirectPath=false)

MountingLocation — Transceiver position offset (m)

[0 0 0] (default) | 1-by-3 vector

Offset of the transmitter origin relative to the Position of the rdrPose platform, specified as a 1-by-3 vector in the form of [x y z], in units of meters. The default value is [0 0 0].

Data Types: double

TransmitterMountingAngles — Transceiver mounting angles (deg)

[0 0 0] (default) | 1-by-3 vector

Transmitter mounting angles relative to the Orientation of the rdrPose platform, specified as a 1-by-3 vector in the form of Euler angles around [z y x] axes, in units of degrees. These angles are also referred to as [yaw pitch roll]. The default value is [0 0 0].

Data Types: double

PropagationSpeed — Signal propagation speed (m/s)

physconst('LightSpeed') (default) | positive scalar

Signal propagation speed, specified as a positive scalar. Units are in meters per second (m/s). The default propagation speed is the value returned by physconst('LightSpeed'). See physconst for more information.

Example: 3e8

Data Types: double

Output Arguments

propPaths — Propagation paths

1-by-P array of structures

Returns two-way monostatic free space propagation paths. propPaths is a 1-by-P array of path configuration structures, where P is the number of tgtPoses. Propagation paths are in the radar mounting frame. Each propPaths structure describes a propagation path and contains these fields.

Field	Description
PathLength	Propagation path length, specified as a nonnegative scalar in units of meters (m).
PathLoss	Propagation loss along the path, specified as a scalar in units of decibels (dB).
ReflectionCoefficient	Cumulative reflection coefficients for all reflections along the path, specified as a scalar. Reflections along the path might include contributions from scatterers or targets.
AngleOfDeparture	Propagation path angle of departure, specified as a two-element vector in the form of [azimuth; elevation] in units of degrees (deg). The angle of departure is determined in the transmit antenna mounting frame.
AngleOfArrival	Propagation path angle of arrival, specified as a two-element vector in the form of [azimuth; elevation] in units of degrees (deg). The angle of arrival is determined in the receive antenna mounting frame.
DopplerShift	Cumulative Doppler shift along the path, specified as a scalar in units of hertz (Hz).

Version History

Introduced in R2025a