tsaregular
Regular signal of a time-synchronous averaged signal
Syntax
Description
Y = tsaregular(X,fs,rpm,orderList)Y of the time-synchronous averaged (TSA)
signal vector X using sampling rate fs, the
rotational speed rpm, and the orders to be retained
orderList. Y is computed by retaining the
primary frequency, the components in orderList, and their respective
harmonics from X. You can use Y to further
extract condition indicators of rotating machinery for predictive maintenance. For
example, extracting the FM0 indicator from Y
is useful in identifying major changes such as gear tooth breakage or heavy wear in a gear
box.
___ = tsaregular(___,
allows you to specify additional parameters using one or more name-value pair arguments.
You can use this syntax with any of the previous input and output arguments.Name,Value)
tsaregular(___) with no output arguments plots the
time-domain and frequency-domain plots of the raw and regular TSA signals.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
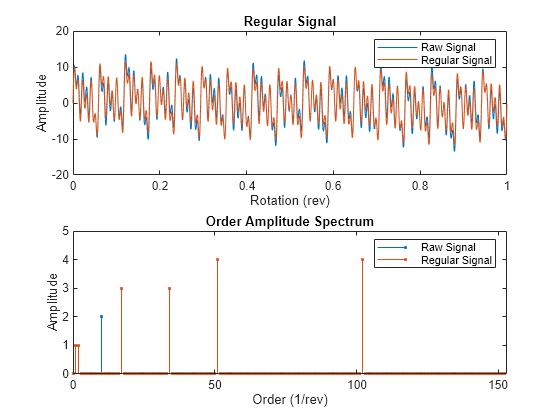
Regular Signal
The regular signal is computed from the TSA signal by retaining the following from the signal spectrum:
Shaft frequency and its harmonics
Gear meshing frequencies and their harmonics
Optionally, the sidebands specified in '
NumSidebands' at the gear meshing frequencies and their harmonics
tsaregular uses a bandwidth equal to the shaft speed times the value of
'NumSidebands', around the frequencies of interest, to compute
Y from the TSA signal. The regular signal is related to the residual
signal through the equation . If the first-order sidebands are retained in the regular signal, then, .
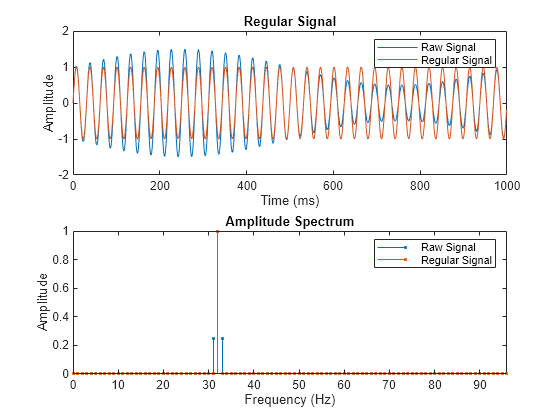
Amplitude Spectrum
The amplitude spectrum of the regular signal is computed as follows,
Here, Y is the regular signal.
References
[1] McFadden, P.D. "Examination of a Technique for the Early Detection of Failure in Gears by Signal Processing of the Time Domain Average of the Meshing Vibration." Aero Propulsion Technical Memorandum 434. Melbourne, Australia: Aeronautical Research Laboratories, Apr. 1986.
[2] Večeř, P., Marcel Kreidl, and R. Šmíd. "Condition Indicators for Gearbox Monitoring Systems." Acta Polytechnica 45.6 (2005), pages 35-43.
[3] Zakrajsek, J. J., Townsend, D. P., and Decker, H. J. "An Analysis of Gear Fault Detection Methods as Applied to Pitting Fatigue Failure Data." Technical Memorandum 105950. NASA, Apr. 1993.
[4] Zakrajsek, James J. "An investigation of gear mesh failure prediction techniques." National Aeronautics and Space Administration Cleveland OH Lewis Research Center, 1989. No. NASA-E-5049.
Extended Capabilities
Version History
Introduced in R2018b