interpolateElectricField
Interpolate electric field in electrostatic or DC conduction result at arbitrary spatial locations
Since R2021a
Syntax
Description
Examples
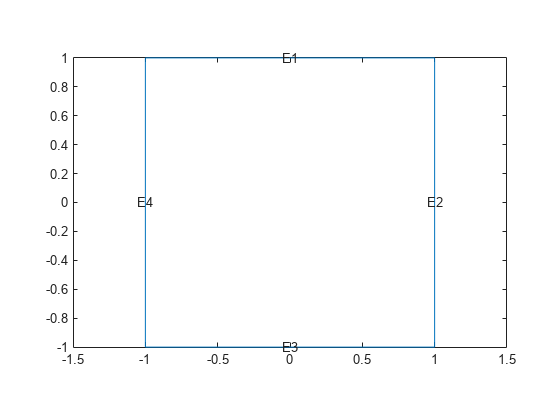
Create a square geometry and plot it with the edge labels.
R1 = [3,4,-1,1,1,-1,1,1,-1,-1]'; g = decsg(R1,'R1',('R1')'); pdegplot(g,EdgeLabels="on") xlim([-1.1 1.1]) ylim([-1.1 1.1])
Create an femodel object for electrostatic analysis and include the geometry into the model.
model = femodel(AnalysisType="electrostatic", ... Geometry=g);
Specify the vacuum permittivity in the SI system of units.
model.VacuumPermittivity = 8.8541878128E-12;
Specify the relative permittivity of the material.
model.MaterialProperties = ...
materialProperties(RelativePermittivity=1);Apply the voltage boundary conditions on the edges of the square.
model.EdgeBC([1 3]) = edgeBC(Voltage=0); model.EdgeBC([2 4]) = edgeBC(Voltage=1000);
Specify the charge density for the entire geometry.
model.FaceLoad = faceLoad(ChargeDensity=5E-9);
Generate the mesh.
model = generateMesh(model);
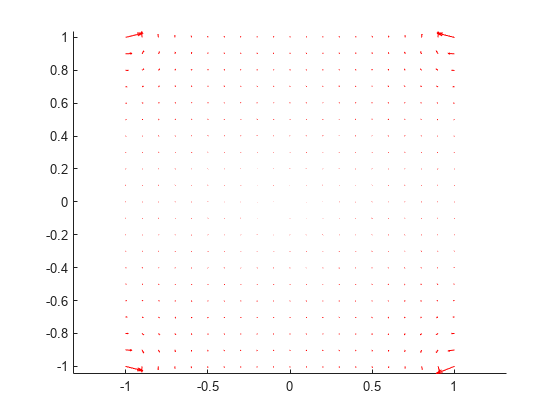
Solve the model and plot the electric field.
R = solve(model); pdeplot(R.Mesh,FlowData=[R.ElectricField.Ex ... R.ElectricField.Ey]) axis equal
Interpolate the resulting electric field to a grid covering the central portion of the geometry, for x and y from -0.5 to 0.5.
v = linspace(-0.5,0.5,51); [X,Y] = meshgrid(v); Eintrp = interpolateElectricField(R,X,Y)
Eintrp =
FEStruct with properties:
Ex: [2601×1 double]
Ey: [2601×1 double]
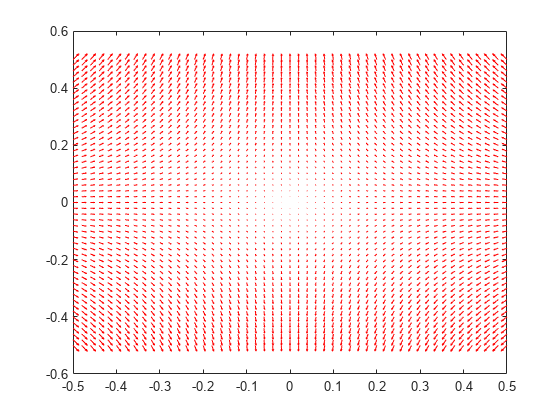
Reshape Eintrp.Ex and Eintrp.Ey and plot the resulting electric field.
EintrpX = reshape(Eintrp.Ex,size(X)); EintrpY = reshape(Eintrp.Ey,size(Y)); figure quiver(X,Y,EintrpX,EintrpY,Color="red") axis equal
Alternatively, you can specify the grid by using a matrix of query points.
querypoints = [X(:),Y(:)]'; Eintrp = interpolateElectricField(R,querypoints);
Create an femodel object for electrostatic analysis and include a geometry of a plate with a hole into the model.
model = femodel(AnalysisType="electrostatic", ... Geometry="PlateHoleSolid.stl");
Plot the geometry.
pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.3)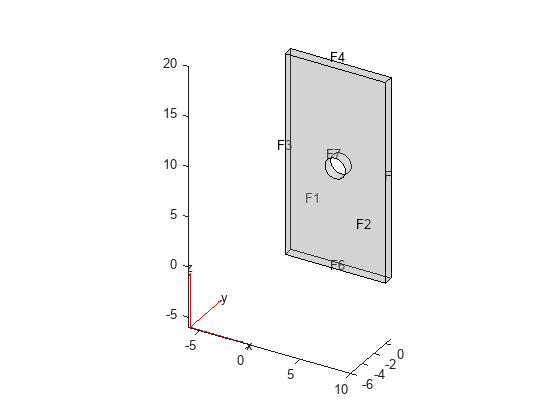
Specify the vacuum permittivity in the SI system of units.
model.VacuumPermittivity = 8.8541878128E-12;
Specify the relative permittivity of the material.
model.MaterialProperties = ...
materialProperties(RelativePermittivity=1);Specify the charge density for the entire geometry.
model.CellLoad = cellLoad(ChargeDensity=5E-9);
Apply the voltage boundary conditions on the side faces and the face bordering the hole.
model.FaceBC(3:6) = faceBC(Voltage=0); model.FaceBC(7) = faceBC(Voltage=1000);
Generate the mesh.
model = generateMesh(model);
Solve the model.
R = solve(model)
R =
ElectrostaticResults with properties:
ElectricPotential: [4747×1 double]
ElectricField: [1×1 FEStruct]
ElectricFluxDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
Plot the electric field.
pdeplot3D(R.Mesh,FlowData=[R.ElectricField.Ex ... R.ElectricField.Ey ... R.ElectricField.Ez])
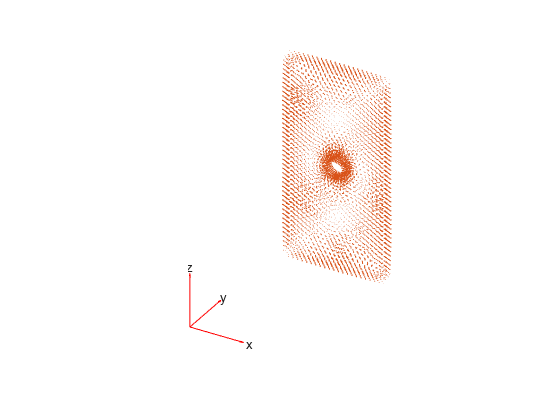
Interpolate the resulting electric field to a grid covering the central portion of the geometry, for x, y, and z.
x = linspace(3,7,7); y = linspace(0,1,7); z = linspace(8,12,7); [X,Y,Z] = meshgrid(x,y,z); Eintrp = interpolateElectricField(R,X,Y,Z)
Eintrp =
FEStruct with properties:
Ex: [343×1 double]
Ey: [343×1 double]
Ez: [343×1 double]
Reshape Eintrp.Ex, Eintrp.Ey, and Eintrp.Ez.
EintrpX = reshape(Eintrp.Ex,size(X)); EintrpY = reshape(Eintrp.Ey,size(Y)); EintrpZ = reshape(Eintrp.Ez,size(Z));
Plot the resulting electric field.
figure
quiver3(X,Y,Z,EintrpX,EintrpY,EintrpZ,Color="red")
view([10 10])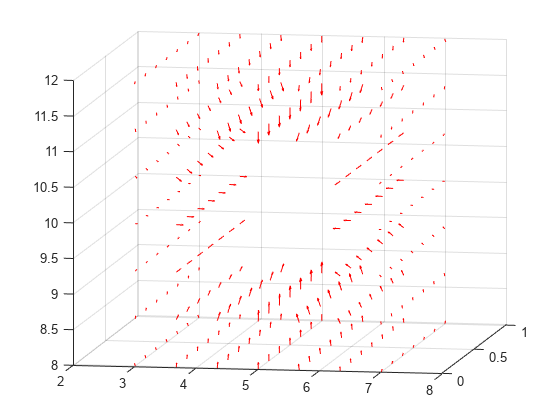
Input Arguments
Solution of an electrostatic or DC conduction problem, specified as an ElectrostaticResults or ConductionResults
object. Create results using the solve
function.
x-coordinate query points, specified as a real array.
interpolateElectricField evaluates the electric field at the 2-D
coordinate points [xq(i) yq(i)] or at the 3-D coordinate points
[xq(i) yq(i) zq(i)] for every i. Because of
this, xq, yq, and (if present)
zq must have the same number of entries.
interpolateElectricField converts the query points to column
vectors xq(:), yq(:), and (if present)
zq(:). It returns electric field values as a column vector of the
same size. To ensure that the dimensions of the returned solution are consistent with
the dimensions of the original query points, use reshape. For
example, use EintrpX = reshape(Eintrp.Ex,size(xq)).
Example: xq = [0.5 0.5 0.75 0.75]
Data Types: double
y-coordinate query points, specified as a real array.
interpolateElectricField evaluates the electric field at the 2-D
coordinate points [xq(i) yq(i)] or at the 3-D coordinate points
[xq(i),yq(i),zq(i)] for every i. Because of
this, xq, yq, and (if present)
zq must have the same number of entries.
interpolateElectricField converts the query points to column
vectors xq(:), yq(:), and (if present)
zq(:). It returns electric field values as a column vector of the
same size. To ensure that the dimensions of the returned solution are consistent with
the dimensions of the original query points, use reshape. For
example, use EintrpY = reshape(Eintrp.Ey,size(yq)).
Example: yq = [1 2 0 0.5]
Data Types: double
z-coordinate query points, specified as a real array.
interpolateElectricField evaluates the electric field at the 3-D
coordinate points [xq(i) yq(i) zq(i)]. Therefore,
xq, yq, and zq must have
the same number of entries.
interpolateElectricField converts the query points to column
vectors xq(:), yq(:), and
zq(:). It returns electric field values as a column vector of the
same size. To ensure that the dimensions of the returned solution are consistent with
the dimensions of the original query points, use reshape. For
example, use EintrpZ = reshape(Eintrp.Ez,size(zq)).
Example: zq = [1 1 0 1.5]
Data Types: double
Query points, specified as a real matrix with either two rows for 2-D geometry or
three rows for 3-D geometry. interpolateElectricField evaluates the
electric field at the coordinate points querypoints(:,i) for every
i, so each column of querypoints contains
exactly one 2-D or 3-D query point.
Example: For a 2-D geometry, querypoints = [0.5 0.5 0.75 0.75; 1 2 0
0.5]
Data Types: double
Output Arguments
Electric field at query points, returned as an FEStruct object
with the properties representing the spatial components of the electric field at the
query points. For query points that are outside the geometry,
Eintrp.Ex(i), Eintrp.Ey(i), and
Eintrp.Ez(i) are NaN. Properties of an
FEStruct object are read-only.
Version History
Introduced in R2021aThe function now interpolates electric field in DC conduction results in addition to electrostatic results.
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)