Output Functions for Optimization Toolbox
What Is an Output Function?
For some problems, you might want output from an optimization algorithm at each iteration. For example, you might want to find the sequence of points that the algorithm computes and plot those points. To do so, create an output function that the optimization function calls at each iteration. See Output Function and Plot Function Syntax for details and syntax.
This example uses the solver-based approach for output functions. For the problem-based approach, see Output Function for Problem-Based Optimization.
Generally, the solvers that employ an output function can take nonlinear functions as inputs. You can determine which solvers can use an output function by looking in the Options section of function reference pages.
Use an Output Function
This example shows how to use an output function to monitor the fmincon solution process for solving a constrained nonlinear optimization problem. At the end of each fmincon iteration, the output function does the following:
Plot the current point.
Store the current point and its corresponding objective function value in a variable named
history, and store the current search direction in a variable namedsearchdir. The search direction is a vector that points in the direction from the current point to the next one.
Additionally, to make the history available outside of the fmincon function, perform the optimization inside a nested function that calls fmincon and returns the output function variables. For more information about this method of passing information, see Passing Extra Parameters. The runfmincon helper function at the end of this example contains the nested function call.
Objective and Constraint Functions
The problem is to minimize the function
subject to the nonlinear inequality constraints
The objfun function nested in runfmincon implements the objective function. The confun function nested in runfmincon implements the constraint function.
Call Solver
To obtain the solution to the problem and see the history of the fmincon iterations, call the runfmincon function.
[xsol,fval,history,searchdir] = runfmincon;
Max Line search Directional First-order
Iter F-count f(x) constraint steplength derivative optimality Procedure
0 3 1.8394 0.5 Infeasible start point
1 6 1.85127 -0.09197 1 0.109 0.778
2 9 0.300167 9.33 1 -0.117 0.313 Hessian modified twice
3 12 0.529835 0.9209 1 0.12 0.232
4 16 0.186965 -1.517 0.5 -0.224 0.13
5 19 0.0729085 0.3313 1 -0.121 0.054
6 22 0.0353323 -0.03303 1 -0.0542 0.0271
7 25 0.0235566 0.003184 1 -0.0271 0.00587
8 28 0.0235504 9.035e-08 1 -0.0146 8.51e-07
Active inequalities (to within options.ConstraintTolerance = 1e-06):
lower upper ineqlin ineqnonlin
1
2
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
<stopping criteria details>
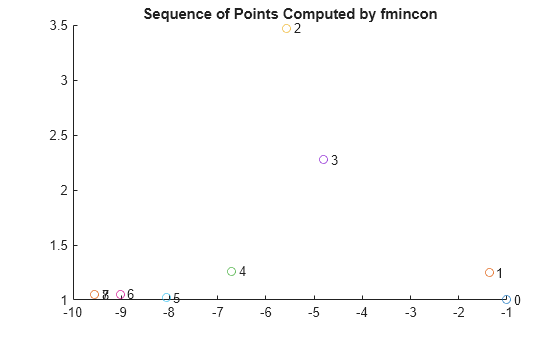
The output function creates a plot of the points evaluated by fmincon. Each point is labeled by its iteration number. The optimal point occurs at the eighth iteration. The last two points in the sequence are so close that they overlap.
The output history is a structure that contains two fields.
disp(history)
x: [9×2 double]
fval: [9×1 double]
The fval field in history contains the objective function values corresponding to the sequence of points fmincon computes.
disp(history.fval)
1.8394
1.8513
0.3002
0.5298
0.1870
0.0729
0.0353
0.0236
0.0236
These same values are displayed in the iterative output in the column with the header f(x).
The x field of history contains the sequence of points that fmincon computes.
disp(history.x)
-1.0000 1.0000 -1.3679 1.2500 -5.5708 3.4699 -4.8000 2.2752 -6.7054 1.2618 -8.0679 1.0186 -9.0230 1.0532 -9.5471 1.0471 -9.5474 1.0474
The searchdir output contains the search directions for fmincon at each iteration. The search direction is a vector pointing from the point computed at the current iteration to the point computed at the next iteration.
disp(searchdir)
-0.3679 0.2500
-4.2029 2.2199
0.7708 -1.1947
-3.8108 -2.0268
-1.3625 -0.2432
-0.9552 0.0346
-0.5241 -0.0061
-0.0003 0.0003
Helper Functions
The following code creates the runfmincon function, which contains the outfun output function, objfun objective function, and confun nonlinear constraint function as nested functions.
function [xsol,fval,history,searchdir] = runfmincon % Set up shared variables with outfun history.x = []; history.fval = []; searchdir = []; % Call optimization x0 = [-1 1]; options = optimoptions(@fmincon,'OutputFcn',@outfun,... 'Display','iter','Algorithm','active-set'); [xsol,fval] = fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options); function stop = outfun(x,optimValues,state) stop = false; switch state case 'init' hold on case 'iter' % Concatenate current point and objective function % value with history. x must be a row vector. history.fval = [history.fval; optimValues.fval]; history.x = [history.x; x]; % Concatenate current search direction with % searchdir. searchdir = [searchdir;... optimValues.searchdirection']; plot(x(1),x(2),'o'); % Label points with iteration number and add title. % Add .15 to x(1) to separate label from plotted 'o'. text(x(1)+.15,x(2),... num2str(optimValues.iteration)); title('Sequence of Points Computed by fmincon'); case 'done' hold off otherwise end end function f = objfun(x) f = exp(x(1))*(4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) +... 2*x(2) + 1); end function [c, ceq] = confun(x) % Nonlinear inequality constraints c = [1.5 + x(1)*x(2) - x(1) - x(2); -x(1)*x(2) - 10]; % Nonlinear equality constraints ceq = []; end end