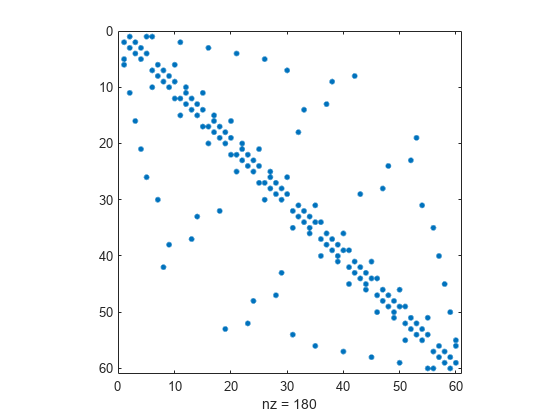
sprand

Sparse uniformly distributed random matrix

Syntax

R = sprand(S)

R = sprand(m,n,density)

R = sprand(m,n,density,rc)

R = sprand(___,typename)

Description

R = sprand(S) creates a sparse matrix that has the same sparsity pattern as the matrix S, but with uniformly distributed random entries.

R = sprand(m,n,density) creates a random m-by-n sparse matrix with approximately density*m*n uniformly distributed nonzero entries for density in the interval [0,1].

R = sprand(m,n,density,rc) creates a matrix that also has reciprocal condition number approximately equal to rc. The matrix R is constructed from a sum of matrices of rank one.

R = sprand(___,typename) returns a sparse matrix of the specified data type. Specify the data type in addition to any of the input argument combinations in previous syntaxes. (since R2025a)

Examples

Create Sparse Matrices with Same Sparsity Pattern

Create the 60-by-60 sparse adjacency matrix of the connectivity graph of the Buckminster Fuller geodesic dome. Plot the sparsity pattern of the matrix S.

S = bucky;
spy(S)

Create another sparse matrix R that has the same sparsity pattern as the matrix S, but with uniformly distributed random entries. Plot the sparsity pattern of R.

R = sprand(S);
spy(R)

Specify Density

Create a random 500-by-1000 sparse matrix with density 0.1. The matrix has approximately 0.1*500*1000 = 50000 uniformly distributed nonzero entries.

R = sprand(500,1000,0.1);

Show the exact number of nonzero elements in the matrix R.

n = nnz(R)

n = 
47663

Specify Reciprocal Condition Number

Create a random 50-by-100 sparse matrix with approximately 0.2*50*100 = 1000 uniformly distributed nonzero entries. Specify the reciprocal condition number of the matrix to be 0.25.

R = sprand(50,100,0.2,0.25);

Show that the condition number of the matrix R is equal to 1/0.25 = 4.

cond(full(R))

ans = 
4.0000

Input Arguments

S — Input matrix

full matrix | sparse matrix

Input matrix, specified as a full or sparse matrix.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes

m — Number of matrix rows

nonnegative integer

Number of matrix rows, specified as a nonnegative integer.

n — Number of matrix columns

nonnegative integer

Number of matrix columns, specified as a nonnegative integer.

density — Density of nonzero elements

scalar

Density of nonzero elements, specified as a scalar. density must be in the interval [0,1].

rc — Reciprocal condition number

scalar | vector

Reciprocal condition number, specified as a scalar or vector. rc must be in the interval [0,1].

If rc is a vector of length lr, where lr <= min(m,n), then R = sprand(m,n,density,rc) has rc as its first lr singular values and all others are zero. In this case, R is generated by random plane rotations applied to a diagonal matrix with the given singular values. It has a great deal of topological and algebraic structure.

typename — Output data type

"double" (default) | "single"

Since R2025a

Output data type, specified as "double" or "single".

Output Arguments

R — Output matrix

sparse matrix

Output matrix, returned as a sparse uniformly distributed random matrix.

Limitations

• sprand is designed to produce large matrices with small density and will generate significantly fewer nonzero values than requested if m*n is small or density is large.

Tips

• sprand uses the same random number generator as the rand, randi, and randn functions. You can control this generator with the rng function.

Extended Capabilities

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The sprand function supports GPU array input with these usage notes and limitations:

• To run this function on a GPU and obtain a gpuArray output, use any of these syntaxes:

  • R = sprand(S), where S is a gpuArray.

  • R = sprand(S,typename), where S is a gpuArray. (since R2025a)

  • R = gpuArray.sprand(S).

  • R = gpuArray.sprand(m,n,density) .

  • R = gpuArray.sprand(___,typename), where typename specifies the data type in addition to the input argument combinations in the two previous syntaxes. (since R2025a)

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Usage notes and limitations:

• See distributed.sprand (Parallel Computing Toolbox).

Version History

Introduced before R2006a

R2025a: Create single-precision sparse matrix

You can specify the output data type by specifying the typename argument as "double" or "single".

R2022a: Improved performance when generating random sparse matrices

The sprand and sprandn functions show improved performance when generating random sparse matrices if the number of nonzero elements in the output is larger than the number of rows.

For example, generating a 10,000-by-10,000 matrix with 10% density of nonzero elements is about 2.5x faster than in the previous release.

function timingSprand
n = 1e4;
d = 0.1; 
rng default

tic
sprand(n,n,d);
toc
end

The approximate execution times are:

R2021b: 2.7 s

R2022a: 1.1 s

The code was timed on a Windows^® 10, Intel^® Xeon^® CPU W-2133 @ 3.60 GHz test system by calling the timingSprand function.