quad2d
Numerically evaluate double integral — tiled method
Description
q = quad2d(fun,a,b,c,d,Name,Value)Name,Value pair
arguments. For example, you can specify 'AbsTol' and
'RelTol' to adjust the error thresholds that the algorithm
must satisfy.
Examples
Integrate
over and .
fun = @(x,y) y.*sin(x)+x.*cos(y); Q = quad2d(fun,pi,2*pi,0,pi)
Q = -9.8696
Compare the result to the true value of the integral, .
-pi^2
ans = -9.8696
Integrate the function
over the region and . This integrand is infinite at the origin (0,0), which lies on the boundary of the integration region.
fun = @(x,y) 1./(sqrt(x + y) .* (1 + x + y).^2 ); ymax = @(x) 1 - x; Q = quad2d(fun,0,1,0,ymax)
Q = 0.2854
The true value of the integral is .
pi/4 - 0.5
ans = 0.2854
quad2d begins by mapping the region of integration to a rectangle. Consequently, it may have trouble integrating over a region that does not have four sides or has a side that cannot be mapped smoothly to a straight line. If the integration is unsuccessful, some helpful tactics are leaving Singular set to its default value of true, changing between Cartesian and polar coordinates, or breaking the region of integration into pieces and adding the results of integration over the pieces.
For instance:
fun = @(x,y)abs(x.^2 + y.^2 - 0.25); c = @(x)-sqrt(1 - x.^2); d = @(x)sqrt(1 - x.^2); quad2d(fun,-1,1,c,d,'AbsTol',1e-8,... 'FailurePlot',true,'Singular',false);
Warning: Reached the maximum number of function evaluations (2000). The result fails the global error test.
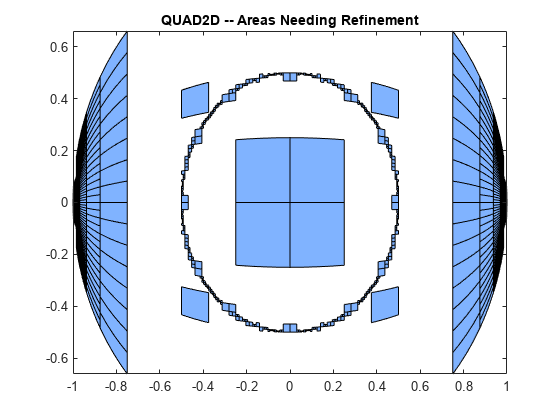
The failure plot shows two areas of difficulty, near the points (-1,0) and (1,0) and near the circle .
Changing the value of Singular to true will cope with the geometric singularities at (-1,0) and (1,0). The larger shaded areas may need refinement but are probably not areas of difficulty.
Q = quad2d(fun,-1,1,c,d,'AbsTol',1e-8, ... 'FailurePlot',true,'Singular',true);
Warning: Reached the maximum number of function evaluations (2000). The result passes the global error test.

From here you can take advantage of symmetry:
Q = 4*quad2d(fun,0,1,0,d,'Abstol',1e-8,... 'Singular',true,'FailurePlot',true)
Q = 0.9817
However, the code is still working very hard near the singularity. It may not be able to provide higher accuracy:
Q = 4*quad2d(fun,0,1,0,d,'Abstol',1e-10,... 'Singular',true,'FailurePlot',true);
Warning: Reached the maximum number of function evaluations (2000). The result passes the global error test.
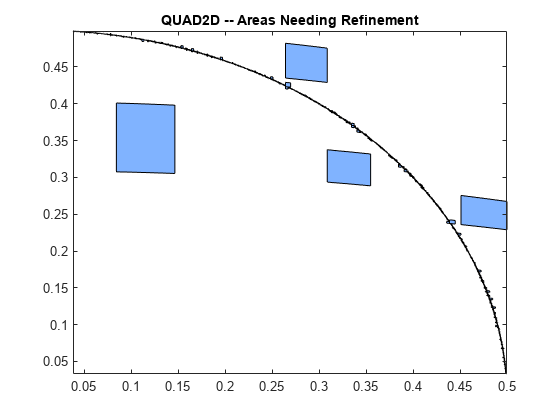
At higher accuracy, a change in coordinates may work better.
polarfun = @(theta,r) fun(r.*cos(theta),r.*sin(theta)).*r;
Q = 4*quad2d(polarfun,0,pi/2,0,1,'AbsTol',1e-10);It is best to put the singularity on the boundary by splitting the region of integration into two parts:
Q1 = 4*quad2d(polarfun,0,pi/2,0,0.5,'AbsTol',5e-11); Q2 = 4*quad2d(polarfun,0,pi/2,0.5,1,'AbsTol',5e-11); Q = Q1 + Q2;
Input Arguments
Function to integrate, specified as a function handle. The function
Z = fun(X,Y) must accept 2-D matrices
X and Y of the same size and
return a matrix Z of corresponding values. Therefore, the
function must be vectorized (that is, you must use elementwise operators
such as .^ instead of matrix operators such as
^). The inputs and outputs of the function must be
either single or double precision.
Example: @(x,y) x.^2 - y.^2
Data Types: function_handle
x limits of integration, specified as scalars.
Data Types: single | double
Complex Number Support: Yes
y limits of integration, specified as scalars or
function handles. Each limit can be specified as a scalar or a function
handle. If the limits are specified as function handles, then they are
functions of the x limit of integration ymin =
@x c(x) and ymax = @(x) d(x). The function
handles ymin and ymax must accept
matrices and return matrices of the same size with the corresponding values.
The inputs and outputs of the functions must be either single or double
precision.
Data Types: single | double | function_handle
Complex Number Support: Yes
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: quad2d(@(x,y) x.*y.^2, 0, 1, 0, 2, 'AbsTol',1e-3)
specifies the absolute tolerance for the integration as
1e-3.
Absolute error tolerance, specified as the comma-separated pair
consisting of 'AbsTol' and a scalar.
quad2d attempts to satisfy ERRBND <=
max(AbsTol,RelTol*|Q|). This is absolute error control
when |Q| is sufficiently small and relative error
control when |Q| is larger. A default tolerance value
is used when a tolerance is not specified. The default value of
AbsTol is 1e-5. The default value of
RelTol is 100*eps(class(Q)).
This is also the minimum value of RelTol. Smaller
RelTol values are automatically increased to the
default value.
Relative error tolerance, specified as the comma-separated pair
consisting of 'RelTol' and a scalar.
quad2d attempts to satisfy ERRBND <=
max(AbsTol,RelTol*|Q|). This is absolute error control
when |Q| is sufficiently small and relative error
control when |Q| is larger. A default tolerance value
is used when a tolerance is not specified. The default value of
AbsTol is 1e-5. The default value of
RelTol is 100*eps(class(Q)).
This is also the minimum value of RelTol. Smaller
RelTol values are automatically increased to the
default value.
Maximum number of evaluations of fun, specified as
the comma-separated pair consisting of 'MaxFunEvals'
and a scalar. Use this option to limit the number of times
quad2d evaluates the function
fun.
Toggle to generate failure plot, specified as the comma-separated pair
consisting of 'FailurePlot' and a numeric or logical
1 (true) or
0 (false). Set
FailurePlot to true or
1 to generate a graphical representation of the
regions needing further refinement when MaxFunEvals
is reached. No plot is generated if the integration succeeds before
reaching MaxFunEvals. The failure plot contains
(generally) 4-sided regions that are mapped to rectangles internally.
Clusters of small regions indicate the areas of difficulty in the
integration.
Toggle to transform boundary singularities, specified as the
comma-separated pair consisting of 'Singular' and a
numeric or logical 1 (true) or
0 (false). By default,
quad2d employs transformations to weaken
boundary singularities for better performance. Set
'Singular' to false or
0 to turn these transformations off, which can
provide a performance benefit on some smooth problems.
Output Arguments
Calculated integral, returned as a scalar.
Error bound, returned as a scalar. The error bound provides an upper bound on the error between the calculated integral q and the exact value of the integral I such that E = | q - I |.
References
[1] L.F. Shampine, "MATLAB Program for Quadrature in 2D." Applied Mathematics and Computation. Vol. 202, Issue 1, 2008, pp. 266–274.
Extended Capabilities
Usage notes and limitations:
Generated code issues a warning if the size of the internal storage arrays is not large enough. If a warning occurs, as a workaround, you can try to divide the region of integration into pieces and sum the integrals over each piece.
Version History
Introduced in R2009a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)